2.18.2 平面中的不同区域

2.18.2.1 函数的定义域

函数的定义域是数组或点的集合, 依函数自变量的取值而定. 按这种方式定义的定义域可大不相同, 通常它们为点的有界或无界连通集. 根据边界是否属于定义域, 定义域分为闭集或开集. 开的连通点集称为区域. 若边界属于定义域, 则称之为闭区域, 若不属于定义域, 有时称为开区域.

2.18.2.2 二维区域

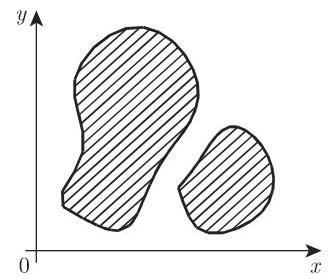
图 2.102 给出了含两个变量的连通点集的最简单情况. 阴影部分表示的是区域; 在图中闭区域即包含边界的区域, 其边界用实线表示; 开区域的边界用虚线表示. 包含全平面在内, 图 2.102 中仅有单连通区域.

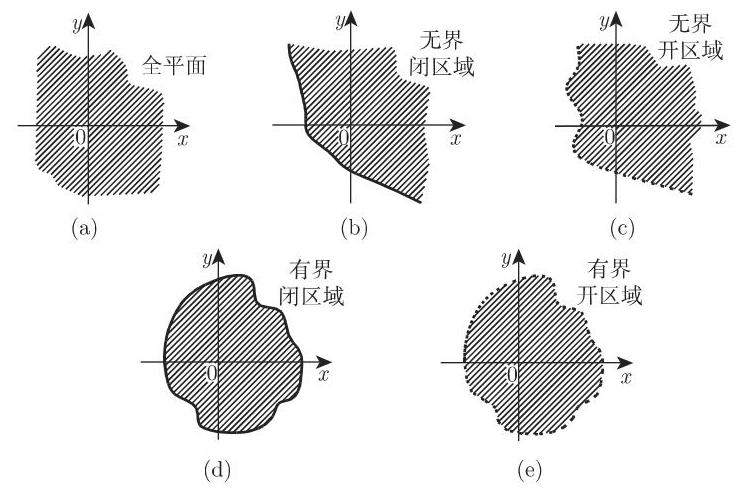
2.18.2.3 三维或多维区域

对三维或多维区域的处理方法与二维类似, 也分为单连通区域和多连通区域. 含三个以上变量的函数可在相应的 $n$ 维空间中进行几何表示.

2.18.2.4 确定函数的方法

1. 数表定义

多元函数可用数表来定义. 关于二元函数的一个例子见椭圆函数积分数表 (参见第 1424 页 21.9). 表的顶部和左侧给出了独立变量的值, 要求的函数值位于相应行和列的交叉位置, 称为复式表.

2. 公式定义

多元函数可用一个或多个公式来定义.

$◼\mathbf{A}$: $u=x{y}^2$ .

$◼\mathbf{B}$: $u=x\ln \left(y-zt\right)$ .

$$\text{ II }:u=\{\begin{array}{ll}x+y,& x\ge 0,y\ge 0,\\ x-y,& x\ge 0,y<0,\\ -x+y,& x<0,y\ge 0,\\ -x-y,& x<0,y<0.\end{array}$$

3. 由公式给出的函数的定义域

在分析中, 大部分这样的函数可由公式来定义, 函数的定义域则为使解析表达式有意义, 即使得解析表达式取得唯一、有限实值的所有数组的并.

定义域举例:

$◼\mathbf{A}$: $u=x^2+y^2$ : 定义域为全平面.

$◼\mathbf{B}$: $u=\frac{1}{\sqrt{16-x^2-y^2}}$ : 定义域为所有满足不等式 $x^2+y^2<16$ 的数组 $x,y$ . 从几何上来看, 该定义域为图 2.103(a) 中圆的内部, 为一个开区域.

$◼\mathbf{C}$: $u=\arcsin \left(x+y\right)$ : 定义域为所有满足不等式 $-1\le x+y\le 1$ 的数组 $x,y$ ,即函数的定义域为图 2.103(b) 中包含在两平行线之间的长条形闭区域.

$◼\mathbf{D}$: $u=\arcsin \left(2x-1\right)+\sqrt{1-y^2}+\sqrt{y}+\ln z$ : 定义域为所有满足不等式 $0\le x\le 1$ , $0\le y\le 1,z>0$ 的数组 $x,y,z$ ,即函数的定义域由位于图 2.103(c) 中边长为 1 的正方形上方的所有三维点 $x,y,z$ 构成.

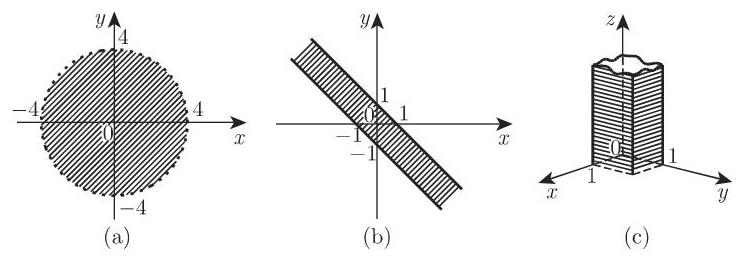
若一点或一有界单连通点集从平面某部分的内部消失, 如图 2.104 所示, 则称之为双连通区域; 图 2.105 表示多连通区域; 图 2.106 为非连通区域.

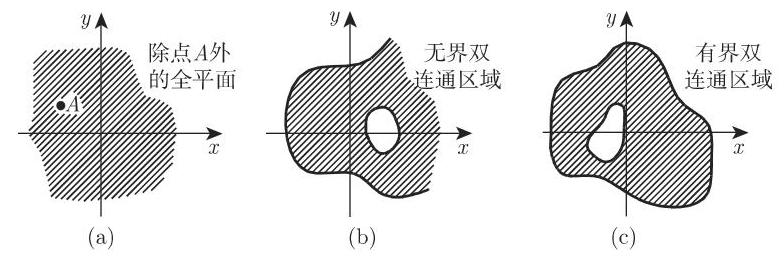
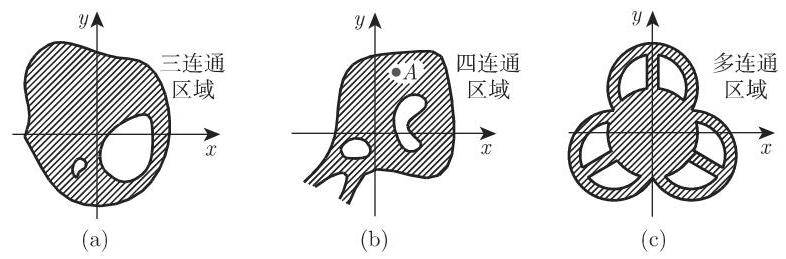
2.18.2.5 函数解析表示的各种形式

正如一元函数, 多元函数可以按不同的方式来定义.

1. 显形式

若函数值 (因变量) 由独立的变量来表示, 即

$$\begin{array}{}\text{(2.277)}& u=f\left(x_1,x_2,\cdots ,x_n\right),\end{array}$$

则称函数由显形式给出或定义.

2. 隐形式

若函数值与自变量的关系按如下方式给出:

$$\begin{array}{}\text{(2.278)}& F\left(x_1,x_2,\cdots ,x_n,u\right)=0,\end{array}$$

且有唯一的 $u$ 满足此等式,则称函数由隐形式给出或定义.

3. 参数形式

若函数和它的 $n$ 个自变量由 $n$ 个新的变量 (参数) 以显形式来定义,且参数和自变量之间一一对应, 则称函数由参数形式给出. 例如对二元函数,

$$\begin{array}{}\text{(2.279a)}& x=\phi \left(r,s\right),y=\psi \left(r,s\right),u=\chi \left(r,s\right);\end{array}$$

对三元函数,

$$\begin{array}{}\text{(2.279b)}& x=\phi \left(r,s,t\right),y=\psi \left(r,s,t\right),z=\chi \left(r,s,t\right),u=\kappa \left(r,s,t\right);\end{array}$$

等等.

4. 齐次函数

多元函数 $f\left(x_1,x_2,\cdots ,x_n\right)$ 称为齐次函数,若对任意 $\lambda$ ,有

$$\begin{array}{}\text{(2.280)}& f\left(\lambda x_1,\lambda x_2,\cdots ,\lambda x_n\right)={\lambda }^{m}f\left(x_1,x_2,\cdots ,x_n\right),\end{array}$$

$m$ 称为齐性次数.

$◼\mathbf{A}$: 若 $u\left(x,y\right)=x^2-3xy+y^2+x\sqrt{xy+\frac{x^3}{y}}$ ,齐性次数 $m=2$ .

$◼\mathbf{B}$: 若 $u\left(x,y\right)=\frac{x+z}{2x-3y}$ ,齐性次数 $m=0$ .

2.18.2.6 函数的相关性

1. 两个函数的特殊情况

定义域 $G$ 相同的两个二元函数 $u=f\left(x,y\right)$ 和 $v=\phi \left(x,y\right)$ 称为相依函数,若其中的一个函数可作为另一个的函数的函数 $u=F\left(v\right)$ 表示出来,即对函数定义域 $G$ 中的每个点,有等式

$$\begin{array}{}\text{(2.281)}& f\left(x,y\right)=F\left(\phi \left(x,y\right)\right)\text{ 或 }\mathrm{\Phi }\left(f,\phi \right)=0\end{array}$$

成立. 若不存在这样的函数 $F\left(\phi \right)$ 或 $\mathrm{\Phi }\left(f,\phi \right)$ ,则称它们为独立函数.

$◼u\left(x,y\right)={(x^2+y^2)}^2,v=\sqrt{x^2+y^2}$ 的定义域为 $x^2+y^2\ge 0$ ,即全平面,因为 $u=v^4$ ,所以二者为相依函数.

2. 多个函数的一般情况

与两个函数的情况类似,具有相同定义域 $G$ 的 $m$ 个 $n$ 元 $x_1,x_2,\cdots ,x_n$ 函数 $u_1,u_2,\cdots ,u_m$ 称为相依函数,若其中一个函数可作为其他函数的函数表示出来,即对函数定义域 $G$ 中的每个点,有等式

$$\begin{array}{}\text{(2.282)}& u_i=f\left(u_1,u_2,\cdots ,u_{i-1},u_{i+1},\dots ,u_m\right)\text{ 或 }\mathrm{\Phi }\left(u_1,u_2,\cdots ,u_m\right)=0\end{array}$$

成立. 若不存在这样的函数关系, 则称它们为独立函数.

$◼$ 函数

$$u=x_1+x_2+\cdots +x_n,v=x_1{}^2+x_2{}^2+\cdots +x_n{}^2,$$$$w=x_1{x}_2+x_1{x}_3+\cdots +x_1{x}_n+x_2{x}_3+\cdots +x_{n-1}{x}_n$$

为相依函数,这是因为 $v=u^2-2w$ 成立.

3. 独立的解析条件

假设下面的每个偏导数都存在. 若两个函数 $u=f\left(x,y\right),v=\phi \left(x,y\right)$ 的函数行列式或雅可比行列式不恒等于零,则它们独立. $n$ 个 $n$ 元函数 $u_1=f_1\left(x_1,\cdots ,x_n\right)$ , $\cdots ,u_n=f_n\left(x_1,\cdots ,x_n\right)$ 的独立性与之类似.

若函数 $u_1,u_2,\cdots ,u_m$ 的个数 $m$ 少于变量 $x_1,x_2,\cdots ,x_n$ 的个数,且矩阵 (2.283c) 中至少有一个 $m$ 阶子式不为零,则函数 $u_1,u_2,\cdots ,u_m$ 独立. 独立函数的个数等于矩阵 (2.283c) 的秩 $r$ (参见第 367 页 4.1.4,7.),这些独立函数的导数构成 $r$ 阶非零行列式的元素. 若 $m>n$ ,则给定的 $m$ 个函数中最多有 $n$ 个独立.

$$\begin{array}{}\text{(2.283a)}& \left|\begin{array}{ll}\frac{\partial f}{\partial x}& \frac{\partial f}{\partial y}\\ \frac{\partial \phi }{\partial x}& \frac{\partial \phi }{\partial y}\end{array}\right|\text{,简记为}\frac{D\left(f,\phi \right)}{D\left(x,y\right)}\text{或}\frac{D\left(u,v\right)}{D\left(x,y\right)}\text{,}\end{array}$$$$\begin{array}{}\text{(2.283b)}& \left|\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \cdots & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \cdots & \frac{\partial f_2}{\partial x_n}\\ ⋮& ⋮& & ⋮\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& \cdots & \frac{\partial f_n}{\partial x_n}\end{array}\right|\equiv \frac{D\left(f_1,f_2,\cdots ,f_n\right)}{D\left(x_1,x_2,\cdots ,x_n\right)}\ne 0.\end{array}$$$$\begin{array}{}\text{(2.283c)}& \left(\begin{array}{cccc}\frac{\partial u_1}{\partial x_1}& \frac{\partial u_1}{\partial x_2}& \cdots & \frac{\partial u_1}{\partial x_n}\\ \frac{\partial u_2}{\partial x_1}& \frac{\partial u_2}{\partial x_2}& \cdots & \frac{\partial u_2}{\partial x_n}\\ ⋮& ⋮& & ⋮\\ \frac{\partial u_m}{\partial x_1}& \frac{\partial u_m}{\partial x_2}& \cdots & \frac{\partial u_m}{\partial x_n}\end{array}\right).\end{array}$$