Appearance
14.4.3 若尔当引理的应用
14.4.3.1 若尔当引理
在许多情形中, 可以用沿一条闭曲线的复积分来计算具有无限积分区间的实反常积分. 为了避免总是反复地估计, 若尔当引理 (Jordan lemma) 被用到形如
的反常积分上,其中
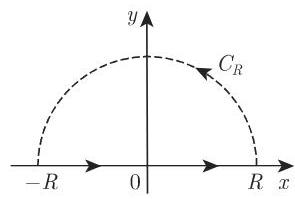
**a)
**b)
**c)
d) 如果用一个弧段代替完整的半圆, 陈述 (14.57b) 亦成立.
e) 当
的积分, 相应于 (14.57b) 的陈述成立.
14.4.3.2 若尔当引理的例子
1. 求积分
对于上面的实积分, 以下述复积分与其相联:
(14.58b)
最后一个积分是复积分
用类似的方法可以计算一些别的积分 (见第 1418 页表 21.8).
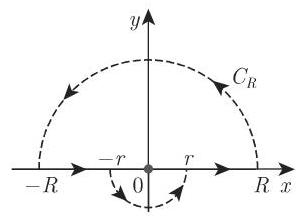
2. 正弦积分 (亦见第 681 页
积分
①这里的
②原文把
3. 阶梯函数
间断的实函数可以表示为复积分. 所谓的阶梯函数 (step function) (亦见第 1011 页 15.2.1.3) 就是一个例子:
符号
如果
4. 矩形脉冲
矩形脉冲 (亦见第 1012 页 15.2.1.3) 是复积分和若尔当引理的又一个例子:
5. 菲涅耳积分
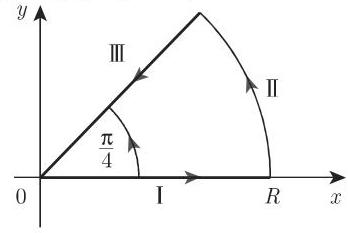
为了推导菲涅耳积分 (Fresnel integral)
必须考察沿展示在图 14.48 中闭积分路径的积分
施行极限过程