Appearance
3.5.3 空间解析几何
3.5.3.1 基本概念
1. 坐标与坐标系
空间中的每个点
最常用的空间坐标系是笛卡儿坐标系、球坐标系和柱坐标系.
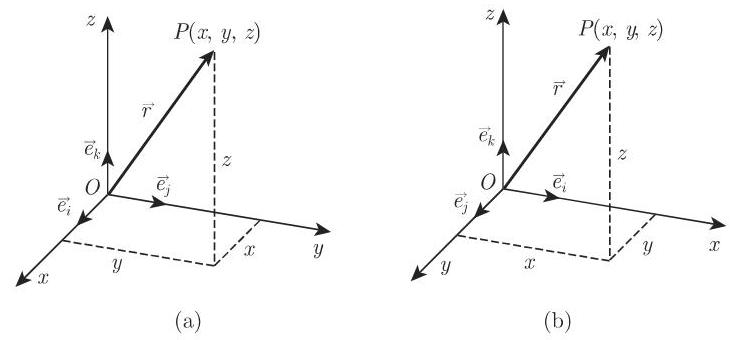
2. 右手系和左手系
右手系和左手系或右手坐标系和左手坐标系的区分依赖于正坐标方向的先后次序. 例如,右手系有三个不共面的单位向量,依下标的字母顺序是
右手系和左手系, 可以通过交换两个单位向量互相变换到对方. 交换两个单位向量将改变其定向: 右手系成为左手系, 反之, 左手系成为右手系.
交换向量的一种非常重要的方法是轮换, 其中定向保持不变. 如图 3.34 所示, 通过轮换交换右手系的向量得到反时针方向的一个旋转,即按图式
一个右手系是不可能叠合在左手系上的.
右手系关于原点的反射是左手系 (参见第 385 页 4.3.5.1, 2.)
3. 笛卡儿坐标
点
卦限 | I | II | III | IV | V | VI | VII | VIII |
在右手笛卡儿坐标系 (图 3.170(a)) 中对于按次序
成立, 即右手法则成立 (参见第 247 页 3.5.1.5). 对单位向量轮换, 这三个公式可以相互变换成另一个.
在左手笛卡儿坐标系 (图 3.170(b)) 中, 等式
成立. 向量积的负号产生自单位向量的左手次序 (图 3.170(b)), 即来自它们的顺时针排列.
注意在两种情形中等式
都成立. 通常我们使用右手坐标系; 公式则不依赖于这种选择. 在大地测量学中常使用左手坐标系 (参见第 191 页 3.2.2.1)
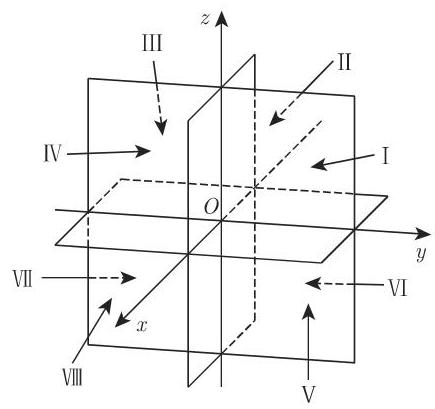
4. 坐标曲面与坐标曲线
坐标曲面具有一个常坐标. 在笛卡儿坐标系中它们是平行于其他两坐标轴所在平面的平面. 通过三个坐标曲面
3.5.3.2 空间坐标系
1. 曲线三维坐标系
如果给定三个曲面族使得空间中任意一点恰有三族曲面中各一个曲面通过它, 则产生一个曲线三维坐标系. 一个点的位置将由通过它的曲面的参数值给出. 最常使用的曲线坐标系是柱坐标系和球坐标系.
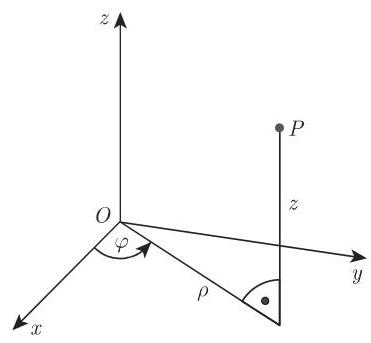
2. 柱坐标系(图 3.172)
包含:
点
在 平面上投影的极坐标 和 以及 点
的竖坐标 .
柱坐标系的坐标曲面是:
具有半径
常数,且以 轴为轴的圆柱面, 从
轴出发的半平面, 常数,以及 垂直于
轴的平面, 常数.
这些坐标曲面的交线是坐标曲线.
笛卡儿坐标系与柱坐标系之间的变换公式 (也见表 3.22) 是
关于
3. 球坐标系(图 3.173)
包含:
点
的向径 的长 , 轴与向径 之间的夹角 ,以及 轴与 在 平面上投影之间的夹角 .
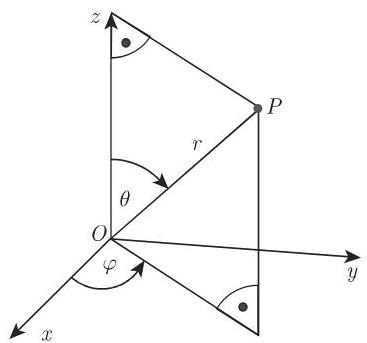
这里的正方向 (图 3.173) 对
球坐标系的坐标曲面是:
以原点
为球心,半径 常数的球面, 常数,顶点在原点,以 轴为轴的圆锥面,以及 从
轴出发的半平面, 常数.
这些坐标曲面的交线是坐标曲线.
4. 笛卡儿坐标、柱坐标和球坐标之间的关系
– 笛卡儿坐标与球坐标之间的变换公式 (也见表 3.22) 是
关于
笛卡儿坐标 | 柱坐标 | 球坐标 |
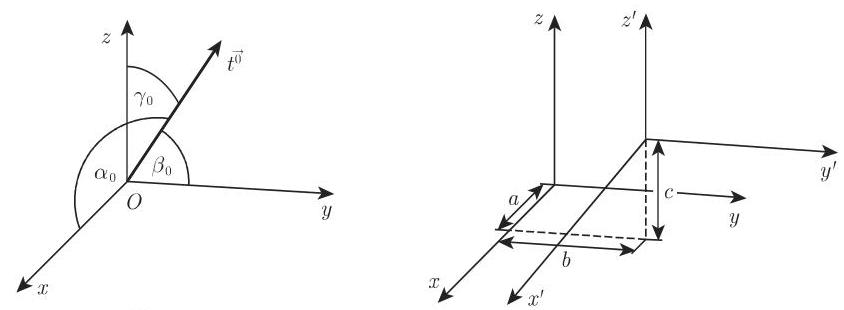
5. 空间中的方向
空间中的一个方向可以用单位向量
由方向余弦
如果
则两个方向相互垂直.
3.5.3.3 正交坐标变换
1. 平移
如果原来的坐标是
2. 坐标系的旋转
旋转后原坐标
给出,
刻画的是
评论
3. 对象的旋转
在几何中区分了两种类型的变换 (也见第 307 页, 3.5.4):
a) 坐标变换 (变换坐标系);
b) 几何变换 (在一个固定坐标系中改变几何对象的位置).
因此, 在绕通过原点的一个任意轴旋转中可以区分出下面两种:
a) 坐标系的旋转 (见
b) 一个对象在一个固定坐标系中的旋转. 在这一情形有
这里,公式 (3.361a),(3.361b) 刻画的是该对象初始位置的坐标
评论 (1) 对围绕通过原点的一个任意轴旋转, 我们将利用四元数作出适当的描述 (参见第 397 页 4.4.2.5).
(2) 我们将在第 312 页的例子中讨论围绕不通过原点的一个任意轴旋转的问题.
3.5.3.4 带有方向余弦的旋转
1. 坐标轴的旋转
如果给定新坐标轴的方向余弦 (如表 3.23, 也见图 3.176), 则对于新、旧坐标有
变换 (3.362a) 的系数矩阵称为旋转矩阵
下列关系成立:
旧坐标轴 | 新坐标轴的方向余弦 | ||
2. 变换行列式的性质
**a)
b) 行或列的元素平方之和总等于 1 .
c) 两个不同的行或列的对应元素乘积之和等于 0 (参见第 368 页 4.1.4, 9.).
d) 每个元素可以写成
3. 标量不变量
在平移和旋转过程中保持其值的标量称为标量不变量. 两个向量的标量积是一个标量不变量 (参见第 247 页3.5.1.5,3.).
因为
3.5.3.5 卡丹角
1. 卡丹角 (Cardan) 的定义
每个围绕通过原点的一个任意轴的坐标系旋转, 可以用三个相继的围绕坐标轴的旋转来刻画. 如果旋转按下面的次序进行 (图 3.176),则旋转角
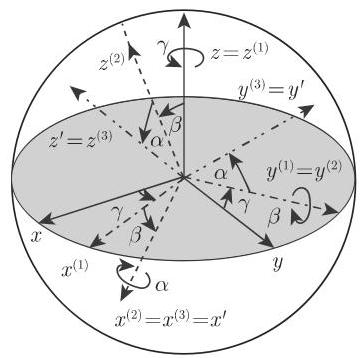
(1) 第一次是围绕
(2)第二次是围绕
(3) 第三次是围绕
评论 文献中给出的卡丹角的定义并不完全相同.
2. 旋转矩阵
由给定的旋转次序
根据法尔克 (Falk) 图式 (也参见第 366 页图 4.1, 图 4.2) 有(3.363b)即(3.363c)
3. 方向余弦作为卡丹角的函数
因为旋转矩阵
其中
3.5.3.6 欧拉角
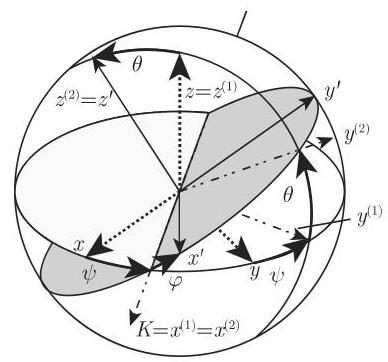
1. 欧拉角的定义
新坐标系相对于旧坐标系的位置, 可以由欧拉引入的三个角唯一确定 (图 3.177).
a) 章动角
b) 进动角
c) 旋转角
评论 在文献中对于欧拉角也使用其他的定义.
2. 旋转矩阵
从坐标系
(1) 第一次是围绕
轴
(2) 第二次是围绕
(3.365b)
(3) 第三次是围绕
它们一起对于 (3.360a) 中的
类似于旋转矩阵
得
(3.366c)
3. 方向余弦作为欧拉角的函数
因为旋转矩阵
其中
3.5.3.7 空间中的特殊量
1. 质心坐标
2. 线段的分割
以给定的比
分
该线段的中点坐标为
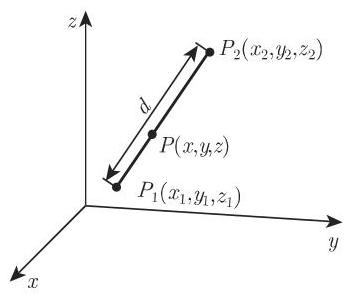
3. 两点之间的距离
图 3.178 中两点
这两点之间线段的方向余弦可以用下面的公式计算:
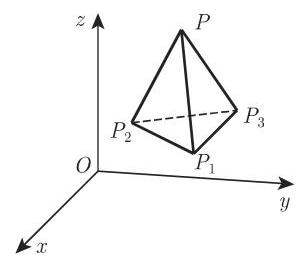
4. 四点系
四个点
其中,如果三个向量
四点共面当且仅当有
3.5.3.8 曲面的方程
方程
常常对应于一个曲面, 并有性质: 它的每个点的坐标满足上述方程. 反之, 坐标满足上述方程的点都是该曲面上的点. 方程 (3.373) 称为该曲面的方程. 如果空间中没有任何实点满足方程 (3.373), 则不存在实曲面.
1. 柱面的方程(参见第 207 页 3.3.4, (1))
柱面方程母线平行于
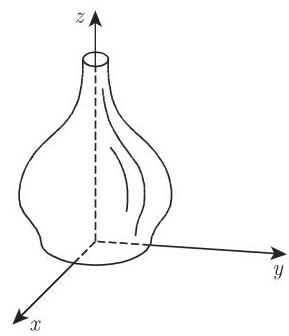
2. 旋转对称曲面的方程
旋转对称曲面是通过在
其他变量情形的旋转对称曲面的方程也可以类似地得到.
具有齐性次数 1,即
3.5.3.9 空间曲线的方程
一条空间曲线可以由三个参数方程
来定义.
对于参数
定义空间曲线的另一种方法是用两个方程
来确定. 两者都定义了一个曲面. 空间曲线包含的是所有坐标满足两个方程的点, 即空间曲线是两个给定曲面的交线. 一般来说,对于任意的
的每个方程都定义了通过所考虑的曲线的一个曲面, 因此, 它可以替换 (3.377) 中的任何一个方程.
3.5.3.10 空间中的直线和平面
1. 平面方程
每个坐标线性方程都定义了一个平面, 反之, 每个平面都具有一个一次方程.
(1) 平面的一般方程
a) 坐标形式
b) 向量形式 *
其中向量
*关于两个向量的标量积参见第 247 页 3.5.1.5, 按仿射坐标给出的标量积参见第 250 页 3.5.1.6, 5.; 关于平面的向量方程参见第 252 页 3.5.1.7.
如果
(2)平面方程的黑赛法式
a)坐标形式
b) 向量形式
其中
(3.380c)
得到. 这里
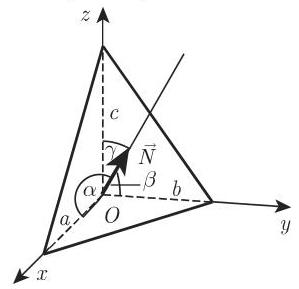
(3)平面方程的截距式 线段
(4) 通过三点的平面方程
如果点是
a) 坐标形式
b) 向量形式
(5) 通过两点且平行于一条直线的平面方程 通过两点
†关于三个向量的混合积见第 249 页 3.5.1.6, 2.
b) 向量形式*
(6) 通过一点且平行于两条直线的平面方程 如果直线的方向向量是
a) 坐标形式
b) 向量形式*
(7) 通过一点且垂直于一条直线的平面方程 如果点是
a) 坐标形式
b) 向量形式
(8) 点到平面的距离 在平面方程的黑赛法式 (3.380a)
中代入点
如果
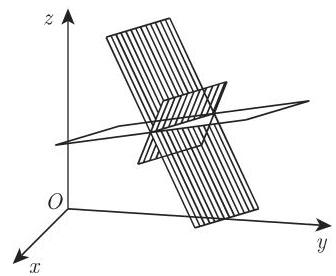
(9) 通过两平面交线的平面方程 通过由方程
a) 坐标形式
b) 向量形式
这里
*关于三个向量的混合积见第 249 页 3.5.1.6, 2.
† 关于两个向量的标量积见第 247 页 3.5.1.5, 1.; 按仿射坐标给出的标量积见第 250 页 3.5.1.6, 5.; 关于平面的向量方程见第 252 页 3.5.1.7.
2. 空间中的两个和多个平面
(1) 两平面之间的夹角,一般情形 由方程
如果两平面由向量方程
(2) 三个平面的交点 三个给定的平面
计算, 其中
如果有
3. 两平面平行和垂直的条件
a) 平行的条件 如果有
成立, 则两平面平行. b) 垂直的条件 如果有
成立, 则两平面互相垂直.
4. 四个平面的交点
四个平面
成立. 在此情形该公共点由三个方程确定, 第四个方程是多余的, 它可以由其他方程导出.
5. 两平行平面之间的距离
如果由方程
给出的两平面平行, 则它们之间的距离是
3.5.3.11 空间中的直线
1. 直线的方程
(1)空间直线的方程, 一般情形 因为空间中的直线可以定义为两个平面的交线, 所以它可以表示为两个线性方程形成的方程组.
a) 坐标形式
b) 向量形式
(2)两投影平面中的直线方程 两个方程
每一个都定义了一个平面,它们过该直线并分别垂直于
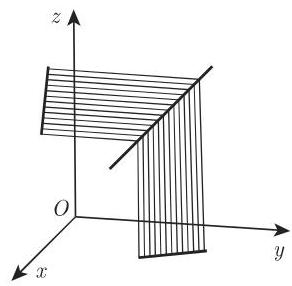
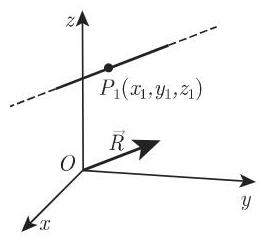
(3) 通过一点平行于一个方向向量的直线方程 通过一点
a) 坐标表示和向量形式
b) 参数形式和向量形式
其中数
或按向量形式
(4) 通过两点的直线方程 通过两点
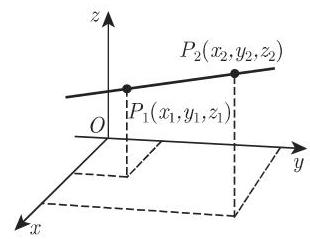
坐标形式和向量形式*
**a)
**b)
如果
(5) 过一点且垂直于一个平面的直线方程 过点
坐标形式和向量形式
**a)
**b)
如果有
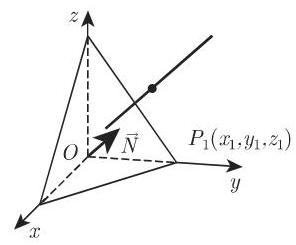
2. 点到直线距离的坐标形式
点
*关于向量积见第 247 页 3.5.1.5.
3. 由坐标形式给出的两直线之间的最短距离
如果两直线是由方程 (3.397a) 给出, 则它们的距离是
如果分子中的行列式等于 0 , 则两直线相交.
3.5.3.12 空间中直线与平面的交点和夹角
1. 直线与平面的交点
(1) 坐标形式的直线方程 由方程
其中
如果
(2) 两投影平面中的直线方程 由方程
如果
(3) 两直线的交点 如果两条直线由
仅当
时交点存在, 否则两直线不相交.
2. 平面和直线之间的夹角
(1)两条直线之间的夹角
a) 一般情形 如果直线由方程
或
b) 平行的条件 如果有
则两条直线平行.
c) 垂直的条件 如果有
则两条直线互相垂直. (2)直线与平面之间的夹角
a) 如果直线和平面由方程
或
b) 平行的条件 如果有
则直线与平面平行.
c) 垂直的条件 如果有
则直线与平面垂直.
3.5.3.13 二次曲面, 标准方程
1. 有心曲面
下面的方程, 也称为二次曲面方程的标准形式, 可以从二次曲面的一般方程通过将中心放置在原点导出 (参见第 306 页 3.5.3.14). 这里中心是通过它的弦的中点. 坐标轴是曲面的对称轴, 因此坐标面也是对称平面.
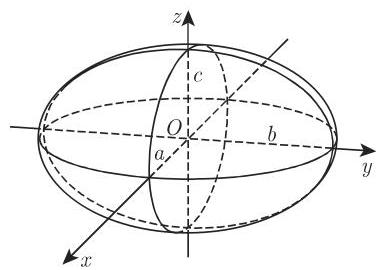
2. 椭球面
设半轴是
需要区分下列特殊情况:
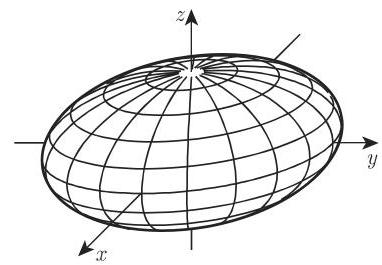
a) 压缩的旋转椭球面(透镜形式)
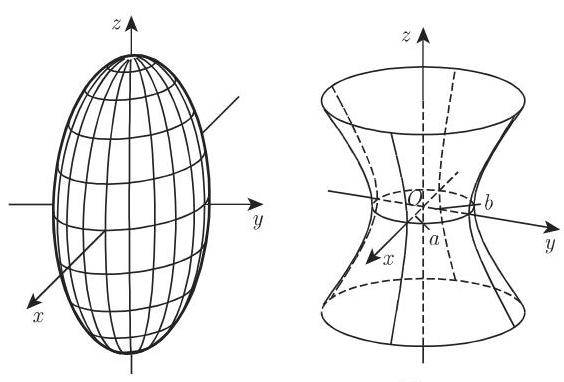
b) 拉伸的旋转椭球面(雪茄形式)
c) 球面
旋转椭球面的两种形式通过
3. 双曲面
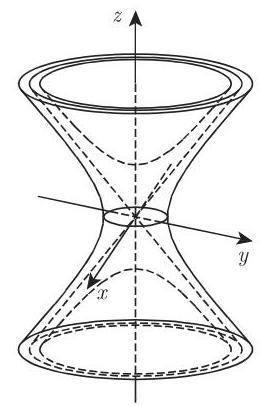
a) 单叶双曲面 (图 3.190) 设
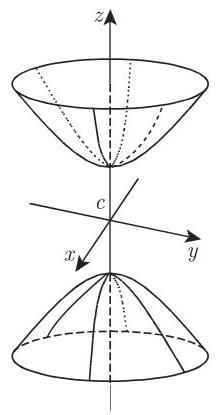
b) 双叶双曲面 (图 3.191) 设
在双曲面的两种情形中,用平行于
当
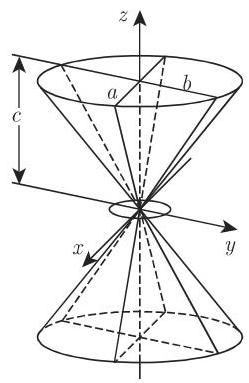
4. 锥面 (图 3.192)
如果顶点在原点, 则方程是
作为准线可以考虑具有半轴
的渐近锥面,它的母线在无穷远处无限趋近于两个双曲面 (图 3.193). 当
5. 抛物面
因为抛物面没有中心,所以在下节中假设顶点在原点,
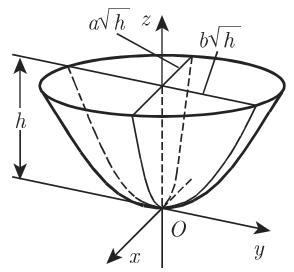
a) 椭圆抛物面(图 3.194)
平行于
垂直于
参数
b) 旋转抛物面 当
c) 双曲抛物面 (图 3.195)
平行于
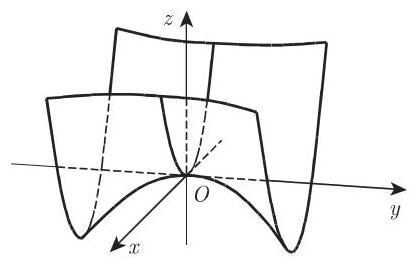
6. 直纹曲面
直纹曲面的直母线完全位于该曲面上. 例子有锥面和柱面的母线.
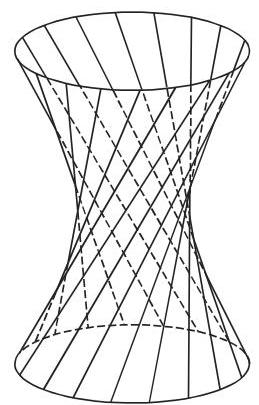
a) 单叶双曲面 (图 3.196)
单叶双曲面具有两族直母线, 方程为
其中
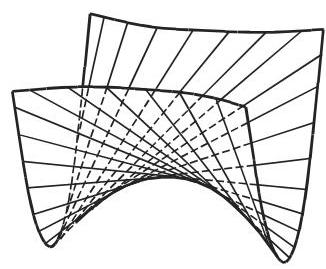
b) 双曲抛物面 (图 3.197)
双曲抛物面也具有两族直母线, 方程为
量
7. 柱面
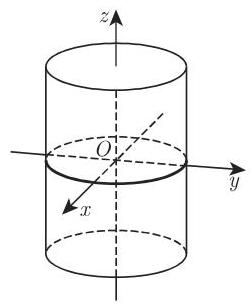
a) 椭圆柱面 (图 3.198)
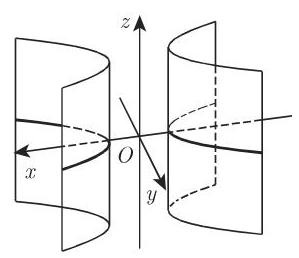
b) 双曲柱面 (图 3.199)
c) 抛物柱面 (图 3.200)
3.5.3.14 二次曲面, 一般理论
1. 二次曲面的一般方程
2. 从其方程判断二次曲面的类型
二次曲面的类型可以从其方程出发利用其不变量
椭球面 | 双叶双曲面 | |
3. 二次曲面的不变量
替换
这些不变量在坐标系的平移或旋转过程中不变.
椭圆抛物面 | 双曲抛物面 | |