5.5.4 密码体制的安全

密码分析学涉及在不知道密钥的情形尽可能多地从密文产生关于明文的信息的方法. 依克尔克霍夫 (A. Kerkhoff) 的观点, 密码体制的安全仅仅依赖于探测密钥或 (更确切地说) 解密函数的困难性. 安全性必须与加密算法保持机密的假设无关. 有以下几种不同的评估密码体制的安全性的方法:

(1)绝对安全密码体制 仅有一种基于代换密码的绝对安全密码体制, 即一次一密发射. 这是香农作为他的信息理论的一个部分证明的.

(2)解析安全密码体制 不存在系统地破译密码体制的方法. 这种方法不存在性的证明可以从解码函数的不可计算性的证明推出.

(3) 基于复杂性理论判据的安全密码体制 不存在多项式时间 (相对于文本的长度) 破译密码体制的算法.

(4) 实用安全密码体制 尚不知道可以用来以有效的资源和满意的成本破译密码体制的方法.

密码分析常使用统计方法, 如确定字母和字的频率. 其他的方法有彻底搜索、尝试法, 以及密码体制的结构分析 (解方程组).

为了破解一个密码体制, 我们可以从加密频率流获益, 例如, 应用立体型短语、 重复传输稍加修改的文本、选取非真实及可预料密钥, 以及应用填充符号.

5.5.4.1 协议密码学方法

除应用密码函数外,还可能用保密码加密明文. 一个码是从字母表 $A$ 上所有字的集合的某个子集 $A^{\prime }$ 到字母表 $B$ 上所有字的集合的某个子集 $B^{\prime }$ 上的一一映射. 这种映射的所有信源-终点对的集合称为一个码本.

今晚 0815

明晚 1113

用短密文代替长密文的优点与相同的明文总是用相同的密文来代替的缺点形成对照. 码本的另一个缺点是完全更换所有码本需要高昂的成本, 甚至可能使码部分地遭到损害.

下面我们只考虑用密码函数加密. 密码函数还有其他优点: 它们不要求在交换前对消息的内容作任何排列.

对换和代换组成密码算法. 在密码学中, 对换是一种定义在几何模型上的特殊的置换. 现在对代换进行细致的讨论. 依据一个字母或多个字母用来呈现密文, 单一字母代换与多字母代换之间存在着差别. 一般地, 代换是对多字母而言 (甚至只使用一个字母), 但单个明文字母的加密与它在明文中的位置有关.

此外, 区分单一字母代换与多字母代换是非常有意义的. 在前一情形单个字母被代换,在后一情形,是固定长度 $>1$ 的字母串被代换.

5.5.4.2 线性代换密码

设 $A=\left\{a_0,a_1,\cdots ,a_{n-1}\right\}$ 是一个字母表, $k,s\in \{0,1,\cdots ,n-1\}$ ,并且 $gcd\left(k,n\right)=1$ . 将每个字母 $a_i$ 映为 $t_s^k\left(a_i\right)=a_{ki+s}$ 的置换 $t_s^k$ 称为线性代换密码. 存在 $n\phi \left(n\right)$ 个 $A$ 上的线性代换密码.

移位密码是 $k=1$ 的线性代换密码. $s=3$ 的移位密码已经被凯撒 (Julius Caesar, 公元前 100 年一前 44 年) 使用过, 所以称作凯撒密码.

5.5.4.3 Vigenère 密码

所谓 Vigenère 密码的加密是基于字母两两不同的密钥的周期应用. 明文字母译为密码由密钥字母确定, 密钥字母在密钥中的位置与这个明文字母在明文中的位置相同. 这就要求密钥与明文一样长. 较短的密钥要加以重复使得与明码的长度相匹配.

卡罗尔 (L. Carroll) 创立的 Vigenère 密码的一个变体应用所谓 Vigenère 表 (见下图) 来加密和解密. 每个行表示它的最左边的关键字母的密码. 明文的字母表列在顶行. 加密步骤如下: 设给定关键字母 $\mathrm{D}$ 和明文字母 $\mathrm{C}$ ,那么密文字母可在标着 $\mathrm{D}$ 的行和标着 $\mathrm{C}$ 的列的交叉处找到; 这个密文是 $\mathrm{F}$ . 解密过程与此相反.

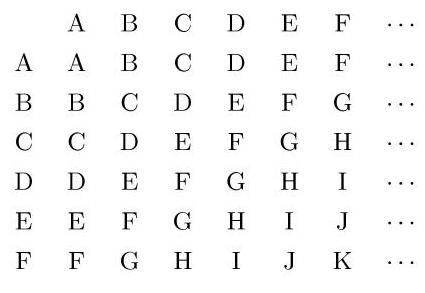
设密钥是 “HUT”.

明文: O N C E U P O N A T I M E

密钥: $\mathrm{H}\mathrm{U}\mathrm{T}\mathrm{H}\mathrm{U}\mathrm{T}\mathrm{H}\mathrm{U}\mathrm{T}\mathrm{H}\mathrm{U}\mathrm{T}\mathrm{H}$

密文: V H V L O I V H T A C F L

从形式上看, Vigenère 密码可以用下列方式写出: 设 $a_i$ 是明文字母, $a_j$ 是对应的密钥字母,那么 $k=i+j$ 确定密文字母 $a_k$ . 在上面的例子中,第一个明文字母是 $\mathrm{O}=a_{14}$ . 密钥的第 15 个位置由字母 $H=a_7$ 取定. 因此 $k=i+j=14+7=21$ 产生密文字母 $a_{21}=V$ .

5.5.4.4 矩阵代换

设 $A=\left\{a_0,a_1,\cdots ,a_{n-1}\right\}$ 是一个字母表,以及 $\mathbf{S}=\left(s_{ij}\right),s_{ij}\in \{0,1,\cdots ,m-$ $1\}$ 是(m, n)型非奇异矩阵,并且 $gcd\left(det\mathbf{S},n\right)=1$ . 将明文区组 $a_{t\left(1\right)},a_{t\left(2\right)},\cdots$ , $a_{t\left(m\right)}$ 映为密文的映射由向量 (要求所有向量按模 $n$ 算术确定分量,并且要转置)(5.274)称作 Hill 密码. 这表示一个单一字母矩阵代换.

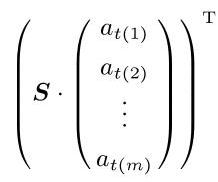
• $S=\left(\begin{array}{ccc}14& 8& 3\\ 8& 5& 2\\ 3& 2& 1\end{array}\right)$ . 设字母表的字母标号为 $a_0=\mathrm{A},a_1=\mathrm{B},\cdots ,a_{25}=\mathrm{Z}$ . 对于 $m=3$ 及明文 AUTUMN,串 AUT 和 UMN 对应于向量(0,20,19)和 (20,12,13). 那么 $\mathbf{S}\cdot {(0,20,19)}^{\mathrm{T}}={(217,138,59)}^{\mathrm{T}}\equiv {(9,8,7)}^{\mathrm{T}}\left(\mathrm{mod}26\right)$ ,以及 $\mathbf{S}\cdot {(20,12,13)}^{\mathrm{T}}={(415,246,97)}^{\mathrm{T}}\equiv {(25,12,19)}^{\mathrm{T}}\left(\mathrm{mod}26\right)$ . 于是明文 AUTUMN 被映为密文 JIHZMT.