14.3.5 孤立奇点和留数定理

14.3.5.1 孤立奇点

如果一个函数中点 $z_0$ 的一个邻域中除了点 $z_0$ 本身外是解析的,则称 $z_0$ 为函数 $f\left(z\right)$ 的一个孤立奇点 (isolated singular point). 如果在 $z_0$ 的邻域中 $f\left(z\right)$ 可以被展开为一个洛朗级数

$$\begin{array}{}\text{(14.51)}& f\left(z\right)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{(z-z_0)}^n,\end{array}$$

则可以根据洛朗级数的性状对孤立奇点加以分类:

1. 如果洛朗级数不包含 $\left(z-z_0\right)$ 的任意负幂次项,即,对于 $n<0$ 有 $a_n=0$ , 则洛朗级数是一个泰勒级数, 其系数由柯西积分定理给出

$$\begin{array}{}\text{(14.52)}& a_n=\frac{1}{2\pi \mathrm{i}}{\oint }_K{(\zeta -z_0)}^{-n-1}f\left(\zeta \right)\mathrm{d}\zeta =\frac{f^{\left(n\right)}\left(z_0\right)}{n!}\left(n=0,1,2,\cdots \right).\end{array}$$

在此情形,函数 $f\left(z\right)$ 本身在点 $z_0$ 处也是解析的,并且 $f\left(z_0\right)=a_0$ ,或者说 $z_0$ 是一个可去奇点.

2. 如果洛朗级数包含 $\left(z-z_0\right)$ 的有限个负幂次项,即,存在 $m>0$ ,使得 $a_{-m}\ne 0$ ,且对于 $n>m$ 有 $a_{-n}=0$ ,则 $z_0$ 被称为一个极点 (pole),一个 $m$ 阶极点 (pole of order $m$ ),或者一个 $m$ 重极点 (pole of multiplicity $m$ ). 乘以 ${(z-z_0)}^m$ , 并且不是乘以任何低次幂, $f\left(z\right)$ 就被变为一个在 $z_0$ 及其邻域中的解析函数.

If $f\left(z\right)=\frac{1}{2}\left(z+\frac{1}{z}\right)$ 在 $z=0$ 处有一个一阶极点.

3. 如果洛朗级数包含 $\left(z-z_0\right)$ 的无穷多个负幂次项,那么 $z_0$ 是 $f\left(z\right)$ 的一个本质奇点 (essential singularity).

趋近于一个极点, $\left|f\left(z\right)\right|$ 趋于无穷. 趋近于一个本质奇点, $f\left(z\right)$ 任意接近于任一复数 $c$ .

$◼$ 函数 $f\left(z\right)={\mathrm{e}}^{1/z}$ ,其洛朗级数为 $f\left(z\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\frac{1}{z^n}$ ,在 $z=0$ 处有一个本质奇点.

14.3.5.2 亚纯函数

如果一个函数在除了一些都是极点的孤立奇点之外是全纯的, 那么这个函数被称为亚纯的 (meromorphic). 亚纯函数总可以表示为两个解析函数之商.

$◼$ 有有限个极点的有理函数,还有如 $\tan z=\frac{\sin z}{\cos z}$ 和 $\cot z=\frac{\cos z}{\sin z}$ 的超越函数是在全平面亚纯的函数的例子.

14.3.5.3 椭圆函数

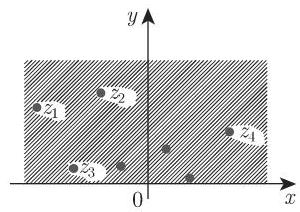
椭圆函数是双周期函数, 它的奇点是极点, 即, 它们是有两个独立周期的亚纯函数 (参见第 995 页 14.6). 如果两个周期是 ${\omega }_1$ 和 ${\omega }_2$ ,它们不是实相关的,则

$$\begin{array}{}\text{(14.53)}& f\left(z+m{\omega }_1+n{\omega }_2\right)=f\left(z\right)\left(m,n=0,\pm 1,\pm 2,\cdots ;\mathrm{Im}\left(\frac{{\omega }_1}{{\omega }_2}\right)\ne 0\right).\end{array}$$

在顶点为 $0,{\omega }_1,{\omega }_1+{\omega }_2,{\omega }_2$ 的原始周期平行四边形中, $f\left(z\right)$ 已遍及其值域.

14.3.5.4 留数

设 $z_0$ 为函数 $f\left(z\right)$ 的一个孤立奇点,则在 $z_0$ 的邻域中成立的 $f\left(z\right)$ 的洛朗展式中 ${(z-z_0)}^{-1}$ 的系数 $a_{-1}$ 被称为在点 $z_0$ 处函数 $f\left(z\right)$ 的留数 (residue of the function $f\left(z\right)$ ). 根据(14.50b),有

$$\begin{array}{}\text{(14.54a)}& a_{-1}={\mathrm{Res}f\left(z\right)|}_{z=z_0}=\frac{1}{2\pi \mathrm{i}}{\oint }_{K}f\left(\zeta \right)\mathrm{d}\zeta .\end{array}$$

由公式

$$\begin{array}{}\text{(14.54b)}& a_{-1}={\mathrm{Res}f\left(z\right)|}_{z=z_0}=\underset{z\to z_0}{lim}\frac{1}{\left(m-1\right)!}\frac{{\mathrm{d}}^{m-1}}{\mathrm{d}{z}^{m-1}}\left[f\left(z\right){(z-z_0)}^m\right]\end{array}$$

可以计算属于一个 $m$ 阶极点的留数. 如果函数可以表示成商 $f\left(z\right)=\phi \left(z\right)/\psi \left(z\right)$ ,其中函数 $\phi \left(z\right)$ 和 $\psi \left(z\right)$ 在点 $z=z_0$ 处是解析的,并且 $z_0$ 是函数 $\psi \left(z\right)$ 的一个单根, 即有 $\psi \left(z_0\right)=0$ ,且 ${\psi }^{\prime }\left(z_0\right)\ne 0$ ,则 $z_0$ 是函数 $f\left(z\right)$ 的一个一阶极点. ${}^{\text{①}}$ 从 (14.54b) 即得

$$\begin{array}{}\text{(14.54c)}& \mathrm{Res}{\left[\frac{\phi \left(z\right)}{\psi \left(z\right)}\right]}_{z=z_0}=\frac{\phi \left(z_0\right)}{{\psi }^{\prime }\left(z_0\right)}.\end{array}$$

如果 $z_0$ 是函数 $\psi \left(z\right)$ 的一个 $m$ 重的根,即成立 $\psi \left(z_0\right)={\psi }^{\prime }\left(z_0\right)=\cdots ={\psi }^{(m-1)}\left(z_0\right)=0$ , 且 ${\psi }^{\left(m\right)}\left(z_0\right)\ne 0$ ,则点 $z=z_0$ 是 $f\left(z\right)$ 的一个 $m$ 阶极点.

---

① 为了 $z_0$ 是函数 $f\left(z\right)$ 的一阶极点,还需加上条件 “ $\phi \left(z_0\right)\ne 0$ ”.——译者注

---

14.3.5.5 留数定理

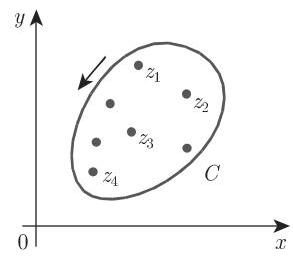
借助于留数可以计算函数在沿着一条包含孤立奇点在其内部的闭曲线(图 14.44) 的积分.

如果在一个其边界为闭曲线 $C$ 的单连通区域 $G$ 中除了有限个点 $z_0,z_1,z_2,\cdots$ , $z_n$ 处外函数 $f\left(z\right)$ 是单值的和解析的,则该函数沿着逆时针方向边界曲线 $C$ 的积分为 $2\pi \mathrm{i}$ 与所有这些奇点处留数之和的乘积:

$$\begin{array}{}\text{(14.55)}& {\oint }_{C}f\left(z\right)\mathrm{d}z=2\pi \mathrm{i}\sum _{k=0}^n{\mathrm{Res}f\left(z\right)|}_{z=z_k}.\end{array}$$

$◼$ 函数 $f\left(z\right)={\mathrm{e}}^z/\left(z^2+1\right)$ 在 $z_{1,2}=\pm \mathrm{i}$ 处有一阶极点. 相应的留数之和为 $\sin 1$ . 如果 $K$ 是以原点为心,半径 $r>1$ 的一个圆周,则

$${\oint }_K\frac{{\mathrm{e}}^z}{z^2+1}\mathrm{d}z=2\pi \mathrm{i}\left(\frac{{\mathrm{e}}^{z_1}}{2z_1}+\frac{{\mathrm{e}}^{z_2}}{2z_2}\right)=2\pi \mathrm{i}\left(\frac{{\mathrm{e}}^{\mathrm{i}}}{2\mathrm{i}}-\frac{{\mathrm{e}}^{-\mathrm{i}}}{2\mathrm{i}}\right)=2\pi \mathrm{i}\sin 1.$$