19.1.1 迭代法

迭代法的基本思路是: 从已知的初始值 $x_k\left(k=0,1,\cdots ,n\right)$ 出发,进一步构造更好的逼近序列, 因此给定方程的解是一个收敛序列的迭代逼近. 构造的序列要有尽可能快的收敛速度.

19.1.1.1 一般迭代法

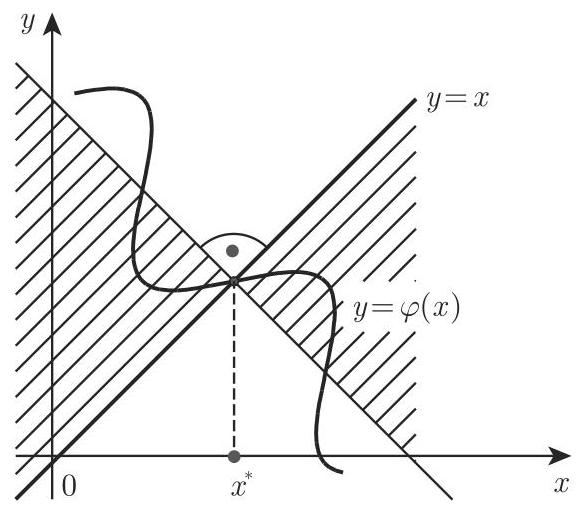
为了求解或许已转化为不动点形式 $x=\phi \left(x\right)$ 的给定方程,迭代法

$$\begin{array}{}\text{(19.3)}& x_{n+1}=\phi \left(x_n\right)\left(n=0,1,\cdots ;x_0\text{ 给定 }\right)\end{array}$$

称为一般迭代法. 如果在 $x^{\ast }$ 邻域内满足

$$\begin{array}{}\text{(19.4)}& \left|\frac{\phi \left(x\right)-\phi \left(x^{\ast }\right)}{x-x^{\ast }}\right|\le K<1,\end{array}$$

其中 $K$ 为常数,而且初值在该邻域内,它将收敛到解 $x^{\ast }$ (图 19.2). 如果函数 $\phi \left(x\right)$ 可导, 则相应的条件变为

$$\begin{array}{}\text{(19.5)}& {\phi }^{\prime }\left(x\right)\le K<1,\end{array}$$

常数 $K$ 越小,一般迭代法的收敛速度越快. $◼x^2=\sin x$ ,即

$$x_{n+1}=\sqrt{\sin x_n}.$$

迭代过程如右表.

$n$	0	1	2	3	4	5
$x_n$	0.87	0.8742	0.8758	0.8764	0.8766	$\underset{―}{0.8767}$
$\sin x_n$	0.7643	0.7670	0.7681	0.7684	0.7686	0.7686

注 (1) 在复数解的情况下,设 $x=u+\mathrm{i}v$ ,分别对实部与虚部组成的两个未知量的方程组求解未知的实数 $u,v$ .

注 (2) 迭代法求解非线性方程组可以参见第 1249 页 19.2.2.

19.1.1.2 牛顿法

1. 牛顿法的公式

为了求解形如 $f\left(x\right)=0$ 的给定方程,最常用到的牛顿法有如下形式:

$$\begin{array}{}\text{(19.6)}& x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}\left(n=0,1,\cdots ;x_0\text{ 给定 }\right).\end{array}$$

即: 为了得到新的近似值 $x_{n+1}$ ,需要计算函数 $f\left(x\right)$ 与其一阶导数 $f^{\prime }\left(x\right)$ 在点 $x_n$ 处的值.

2. 牛顿法的收敛条件

$$\begin{array}{}\text{(19.7a)}& f^{\prime }\left(x\right)\ne 0\end{array}$$

是牛顿法收敛的必要条件, 条件

$$\begin{array}{}\text{(19.7b)}& \left|\frac{f\left(x\right)f^{\prime \prime }\left(x\right)}{f^{\prime 2}\left(x\right)}\right|\le K<1\end{array}$$

是牛顿法收敛的充分条件. 需要在解 $x^{\ast }$ 及其邻域内所有的点 $x_n$ 都满足条件 (19.7a, 19.7b). 如果牛顿法收敛,其收敛速度非常快. 它是平方阶收敛的,即第 $n+1$ 个近似值的误差远小于一个常数乘以第 $n$ 个近似值的误差的平方. 在十进制中,这意味着经过迭代准确值的位数成倍增加.

$◼$ 求解方程 $f\left(x\right)=x^2-a=0$ ,即计算 $x=\sqrt{a}(a>0$ 给定),由牛顿法得到迭代公式为

$$\begin{array}{}\text{(19.8)}& x_{n+1}=\frac{1}{2}\left(x_n+\frac{a}{x_n}\right).\end{array}$$

对于 $a=2$ ,有

$n$	0	1	2	3
$x_n$	1.5	1.4166666	1.4142157	1.4142136

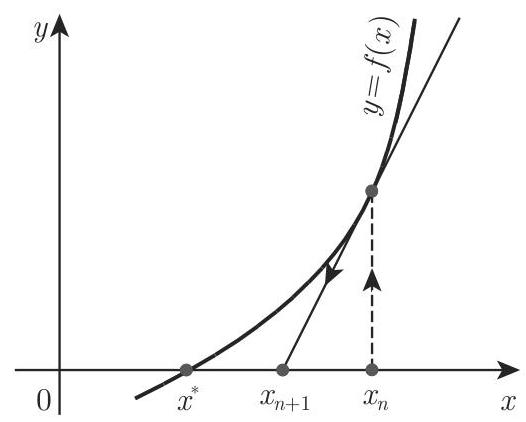
3. 几何插值

牛顿法几何插值可以表示为图 19.3. 牛顿法的基本思想是用函数 $y=f\left(x\right)$ 的切线得到局部近似值.

4. 修正牛顿法

如果在迭代过程中 $f^{\prime }\left(x_n\right)$ 的数值几乎不变,它在一段时间内保持为常数,可用所谓修正牛顿法

$$\begin{array}{}\text{(19.9)}& x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_m\right)}\left(m\text{ 给定,}m<n\right).\end{array}$$

这种简化的好处是其收敛阶几乎没有任何改变.

5. 复变量的可微函数

牛顿法对于复变量的可微函数同样适用.

19.1.1.3 试位法

1. 试位法的公式

为求解形如 $f\left(x\right)=0$ 的方程,试位法具有如下形式:

$$\begin{array}{}\text{(19.10)}& x_{n+1}=x_n-\frac{x_n-x_m}{f\left(x_n\right)-f\left(x_m\right)}f\left(x_n\right)\left(n=1,2,\cdots ;x_0,x_1\text{ 给定,}m<n\right).\end{array}$$

该方法仅需要计算函数值. 该方法源于牛顿法 (19.6),而导数 $f^{\prime }\left(x_n\right)$ 由 $f\left(x\right)$ 在点 $x_n$ 与前一个点 $x_m$ 的有限差分近似得到 $\left(m<n\right)$ .

2. 几何插值

试位法几何插值可以表示为图 19.4. 试位法的基本思想是用曲线 $y=f\left(x\right)$ 的切线得到局部近似值.

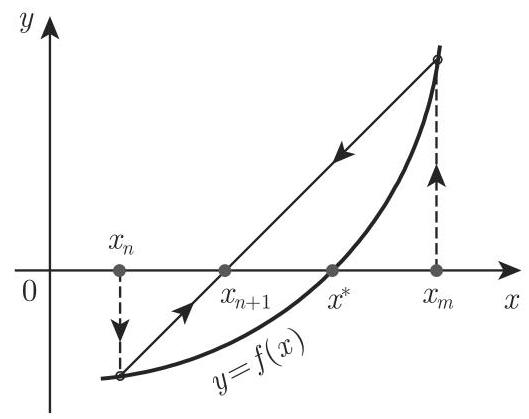
3. 收敛性

当选取的 $m$ 使得 $f\left(x_n\right)$ 和 $f\left(x_m\right)$ 一直是异号时,方法 (19.10) 是收敛的. 若在迭代过程中收敛速度已经足够快,可以忽略符号改变,只要用 $x_m=x_{n-1}$ 就可以增加收敛速度.

• 计算 $f\left(x\right)=x^2-\sin x=0$ .

$n$	$\mathrm{\Delta }{x}_n=x_n-x_{n-1}$	$x_n$	$f\left(x_n\right)$	$\mathrm{\Delta }{y}_n=f\left(x_n\right)-f\left(x_{n-1}\right)$	$\mathrm{\Delta }{x}_n$ $\mathrm{\Delta }{y}_n$
0		0.9	0.0267
1	-0.3	0.87	-0.0074	-0.0341	0.8798
2	0.0065	0.8765	-0.000252	0.007148	0.9093
3	0.000229	0.876729	0.000003	0.000255	0.8980
4	-0.000003	0.876726

如果计算过程中 $\mathrm{\Delta }{x}_n/\mathrm{\Delta }{y}_n$ 的数值几乎不变,就不用一次一次地继续计算了.

4. 斯特芬森方法

应用试位法取 $x_m=x_{n-1}$ 求解方程 $f\left(x\right)=x-\phi \left(x\right)=0$ ,其收敛速度可以提高,尤其是 ${\phi }^{\prime }\left(x\right)<-1$ 的情况. 该算法被称为斯特芬森 (Steffensen) 方法.

应用斯特芬森方法求解 $x^2=\sin x$ ,需要用到 $f\left(x\right)=x-\sqrt{\sin x}=0$ .

$n$	$\mathrm{\Delta }{x}_n=x_n-x_{n-1}$	$x_n$	$f\left(x_n\right)$	$\mathrm{\Delta }y=f\left(x_n\right)-f\left(x_{n-1}\right)$	$\mathrm{\Delta }{x}_n$ $\mathrm{\Delta }{y}_n$
0		0.9	0.014942
1	-0.03	0.87	-0.004259	-0.019201	1.562419
2	0.006654	0.876654	-0.000046	0.004213	1.579397
3		0.876727	0.000001