4.3.5 伪张量

张量的反射在物理学中起着特殊作用. 虽然极向量和轴向量在数学上可以用同样的方法处理, 但由于它们关于反射的不同性状 (参见第 242 页 3.5.1.1, 2.), 所以要加以区分. 极向量和轴向量相互间的差别在于它们的确定, 因为轴向量除了长度和方向外, 可以由定向来表示. 轴向量也称为伪张量. 因为向量可以看作张量, 所以引进伪张量的一般概念.

4.3.5.1 关于原点的对称性

1. 张量在空间反演下的性状

(1)空间反演的概念 空间中点的位置坐标关于原点的反射称作空间反演或坐标反演. 在三维笛卡儿坐标系空间反演意味着坐标变号:

$$\begin{array}{}\text{(4.99)}& \left(x,y,z\right)\to \left(-x,-y,-z\right).\end{array}$$

由此右手坐标系变成左手坐标系. 类似的法则对于其他坐标系也成立. 在球坐标系中, 有

$$\begin{array}{}\text{(4.100)}& \left(r,\theta ,\phi \right)\to \left(-r,\pi -\theta ,\phi +\pi \right).\end{array}$$

在这种类型的反射中向量的长度和向量的夹角不变. 可以通过线性变换进行转换

(2) 变换矩阵 依据 (4.66),三维空间线性变换的变换矩阵 $\mathbf{A}=\left(a_{\mu \nu }\right)$ 在空间反演情形有下列性质:

$$\begin{array}{}\text{(4.101a)}& a_{\mu \nu }=-{\delta }_{\mu \nu },det\mathbf{A}=-1.\end{array}$$

对于 (4.69) 中秩 $n$ 张量的分量,有

$$\begin{array}{}\text{(4.101b)}& {\tilde{t}}_{\mu \nu \cdots \gamma }={(-1)}^n{t}_{\mu \nu \cdots \gamma }.\end{array}$$

这就是说: 在关于原点对称的情形下, 秩 0 张量仍然是标量, 不变; 秩 1 张量仍然是向量, 并且变号; 秩 2 张量保持不变, 等等.

2. 几何表示

三维笛卡儿坐标系中空间反演可分两步实现 (图 4.3):

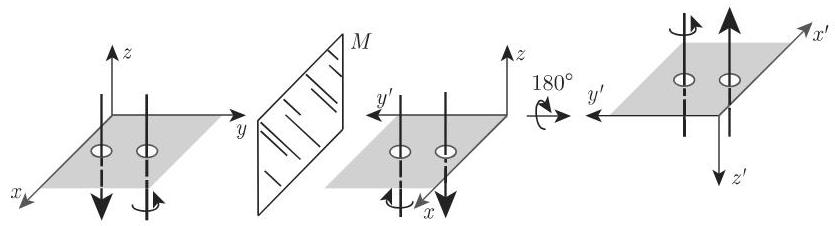
(1) 通过关于坐标平面 (例如 $x,z$ 平面) 的反射,坐标系 $x,y,z$ 变为坐标系 $x,-y,z$ . 右手系变成左手系 (参见第 281 页 3.5.3.1,2.).

(2) 通过坐标系 $x,y,z$ 绕 $y$ 轴旋转 ${180}^{\circ }$ ,我们得到完全的关于原点对称的坐标系 $x,y,z$ . 因为它是实施步骤 (1) 的结果,所以这个坐标系保持为左手系.

结论 空间反演将极向量的定向改变 ${180}^{\circ }$ ,同时保持轴向量的定向.

4.3.5.2 伪张量概念引论

(1)空间反演下的向量积 在空间反演下,两个极向量 $\underset{―}{a}$ 和 $\underset{―}{b}$ 被变为 $-\underset{―}{a}$ 和 $-\underset{―}{b}$ ,即它们的分量满足秩 1 张量的变换公式 (4.101b). 但是如果考虑 (例如) 两个轴向量的向量积 $\underset{―}{c}=\underset{―}{a}\times \underset{―}{b}$ ,那么在关于原点的反射下,我们得到 $\underset{―}{c}=\underset{―}{c}$ . 这违反秩 1 张量的变换公式 (4.101a). 因此轴向量 $\underset{―}{c}$ 称作伪向量,或一般地,称作伪张量.

向量积 $\overrightarrow{r}\times \overrightarrow{v},\overrightarrow{r}\times \overrightarrow{F},\mathrm{\nabla }\times \overrightarrow{v}=\mathrm{rot}\overrightarrow{v}$ 都是轴向量的例子,它们在反射下有 “违规” 性状,其中 $\overrightarrow{r}$ 是位置向量, $\overrightarrow{v}$ 是速度向量, $\overrightarrow{F}$ 是力向量, $\mathrm{\nabla }$ 是那布拉算子.

(2) 空间反演下的标量积 如果对一个极向量和一个轴向量的标量积应用空间反演, 那么又出现违反秩 1 张量的变换公式 (4.101b) 的情形. 因为标量积的结果是一个标量, 并且一个标量在每个坐标系中应当是相同的, 所以在此它是一个特殊的标量, 称作伪标量. 它具有在空间反演下改变符号的性质. 伪标量没有标量的旋转不变性.

极向量 $\overrightarrow{r}$ (位置向量) 和 $\overrightarrow{v}$ (速度向量) 与轴向量 $\overrightarrow{\omega }$ (角速度向量) 的标量积是标量 $\overrightarrow{r}\cdot \overrightarrow{\omega }$ 和 $\overrightarrow{v}\cdot \overrightarrow{\omega }$ ,它们在反射下都有 “违规” 性状,所以是伪标量.

(3) 空间反演下的混合积 依据 (2),极向量 $\underset{―}{a},\underset{―}{b}$ 和 $\underset{―}{c}$ 的混合积 $\left(\underset{―}{a}\times \underset{―}{b}\right)\cdot \underset{―}{c}$ (参见第 249 页 3.5.1.6,2.) 是伪标量,因为因子 $\left(\underset{―}{\mathbf{a}}\times \underset{―}{\mathbf{b}}\right)$ 是一个轴向量. 混合积在空间反演下变号.

(4) 伪向量和秩 2 斜对称张量 依据 (4.74b),轴向量 $\underset{―}{\mathbf{a}}={(a_1,a_2,a_3)}^{\mathrm{T}}$ 和 $\underset{―}{\mathbf{b}}={(b_1,b_2,b_3)}^{\mathrm{T}}$ 的张量积生产一个秩 2 张量,其分量 $t_{ij}=a_i{b}_j\left(i,j=1,2,3\right)$ . 因为每个秩 2 张量可以分解为秩 2 对称张量和斜对称张量之和, 所以依据 (4.81) 有

$$\begin{array}{}\text{(4.102)}& t_{ij}=\frac{1}{2}\left(a_i{b}_j+a_j{b}_i\right)+\frac{1}{2}\left(a_i{b}_j-a_j{b}_i\right)\left(i,j=1,2,3\right).\end{array}$$

(4.102) 中斜对称部分恰好是向量积 $\left(\underset{―}{a}\times \underset{―}{b}\right)$ 的分量与 $\frac{1}{2}$ 的乘积,所以分量为 $c_1,c_2,c_3$ 的轴向量 $\underset{―}{\mathbf{c}}=\left(\underset{―}{\mathbf{a}}\times \underset{―}{\mathbf{b}}\right)$ 可以看作斜对称秩 2 张量

$$\begin{array}{}\text{(4.103a)}& \mathbf{C}=\underset{―}{\mathbf{c}}=\left(\begin{array}{ccc}0& c_{12}& c_{13}\\ -c_{12}& 0& c_{23}\\ -c_{13}& -c_{23}& 0\end{array}\right),\end{array}$$

其中

$$c_{23}=a_2{b}_3-a_3{b}_2=c_1,$$$$\begin{array}{}\text{(4.103b)}& c_{31}=a_3{b}_1-a_1{b}_3=c_2,\end{array}$$$$c_{12}=a_1{b}_2-a_2{b}_1=c_3,$$

它的分量满足秩 2 张量的变换公式 (4.101b). 因此, 每个轴向量 (伪向量或伪秩 1 张量) $\underset{―}{\mathbf{c}}={(c_1,c_2,c_3)}^{\mathrm{T}}$ 可以看作秩 2 斜对称张量 $\mathbf{C}$ :

$$\begin{array}{}\text{(4.104)}& \mathbf{C}=\underset{―}{\mathbf{c}}=\left(\begin{array}{ccc}0& c_3& -c_2\\ -c_3& 0& c_1\\ c_2& -c_1& 0\end{array}\right).\end{array}$$

(5) 秩 $n$ 伪张量 伪标量和伪向量概念的推广是秩 $n$ 伪张量. 在旋转变换下它有与秩 $n$ 张量相同的性质 (旋转矩阵 $\mathbf{D}$ 的行列式 $det\mathbf{D}=1$ ),但它在关于原点反射后有一个因子(-1). 高秩伪张量的例子可在文献,例如,[4.2] 中找到.