18.1.3 单纯形法

18.1.3.1 单纯形表

单纯形法用于产生可行集的一列极端点, 其对应的目标函数值不断增加. 为了从给定的一个极端点找出一个新的极端点, 我们从对应于给定极端点的规范形出发, 逐步到达对应于新的极端点的规范形. 为了有一个清晰的排列, 以及比较容易理解相应数字的含义, 我们将规范形 (18.9a, 18.9b) 重新表示成单纯形表 (表 18.2(a), 表 18.2(b)).

表中的第 $k$ 行对应于约束

$$\begin{array}{}\text{(18.15a)}& x_{n-m+k}+a_{k,1}{x}_1+\cdots +a_{k,n-m}{x}_{n-m}=b_k.\end{array}$$

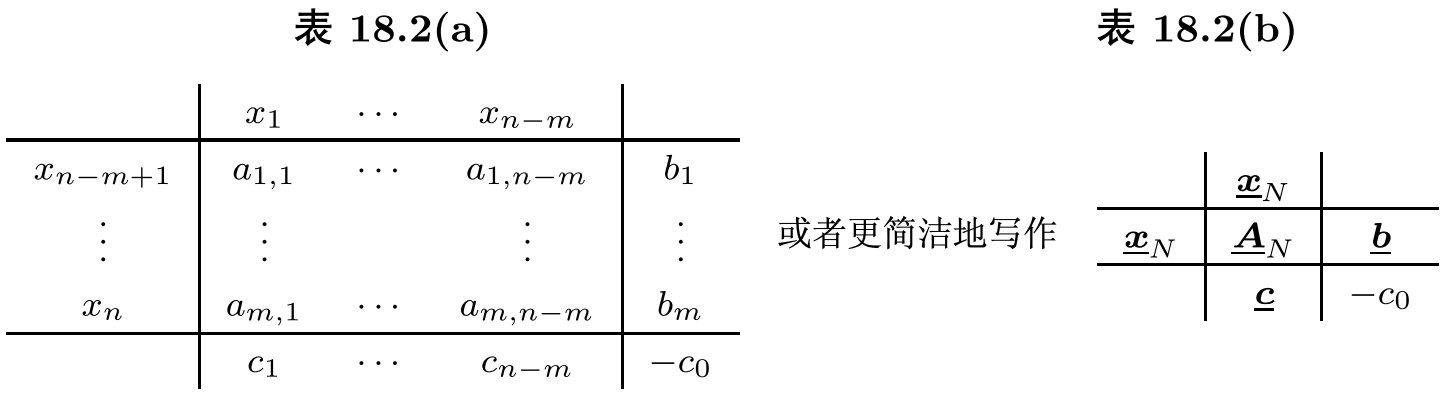
目标函数是

$$\begin{array}{}\text{(18.15b)}& c_1{x}_1+\cdots +c_{n-m}{x}_{n-m}=f\left(\underset{―}{\mathbf{x}}\right)-c_0.\end{array}$$

从这个单纯形表,就能找出极端点 $\left({\underset{―}{x}}_N,{\underset{―}{x}}_B\right)=\left(\underset{―}{0},\underset{―}{b}\right)$ . 目标函数在这个极端点上的值是 $f\left(\underset{―}{\mathbf{x}}\right)=c_0$ . 把 $-c_0$ 放到表的右下端有利于进行单纯形方法的计算. 在每一个表中总能找出如下三种情形中的一种:

**a) $c_j\ast \ast \le 0,j=1,\cdots ,n-m$ : 这样的表是最优的. 点 $\left({\underset{―}{\mathbf{x}}}_N,{\underset{―}{\mathbf{x}}}_B\right)=\left(\underset{―}{\mathbf{0}},\underset{―}{\mathbf{b}}\right)$ 是极大点. 如果所有 $c_j$ 是正的,那么这个顶点是唯一的极大点.

b) 至少有一个 $j$ 使得 $c_j>0$ ,并且 $a_{ij}\le 0,i=1,\cdots ,m$ : 线性规划问题没有解,因为目标函数在可行集上无界; 随着 $x_j$ 的增加,它会无穷增加.

c) 对于每个使得 $c_j>0$ 的 $j$ ,至少有一个 $i$ 使得 $a_{ij}>0$ : 有可能从极端点 $\underset{―}{x}$ 移动到邻近的极端点 $\underset{―}{x}$ 时 $f\left(\underset{―}{x}\right)\ge f\left(\underset{―}{x}\right)$ . 在非退化极端点 $\underset{―}{x}$ 的情形下, “>” 号总是成立的.

18.1.3.2 过渡到新的单纯形表

1. 非退化情形

如果一个表不是上述最后的情形 (情形 c), 那么新的表就按如下方式确定 (表 18.3). 基变量 $x_p$ 和非基变量 $x_q$ 之间通过下列计算进行转换:

元 $a_{pq}$ 称作主元,第 $p$ 行为主行,而第 $q$ 列为主列. 为了选择主元,需要考虑如下两个要求:

a) 应该有 ${\tilde{c}}_0\ge c_0$ ;

b) 新的表也必须对应于一个可行解,即必须有 $\widetilde{\underset{―}{b}}\ge \underset{―}{0}$ .

于是 $\left({\underset{―}{\tilde{\mathbf{x}}}}_N,{\underset{―}{\tilde{\mathbf{x}}}}_B\right)=\left(\underset{―}{\mathbf{0}},\underset{―}{\tilde{b}}\right)$ 是一个新的极端点,在此极端点上目标函数取值 $f\left(\underset{―}{\tilde{\mathbf{x}}}\right)=$ ${\tilde{c}}_0$ 不小于以前的值. 如果主元按如下方式选择,则这些条件满足:

a) 为增加目标函数的值,可以选择对应于 $c_q>0$ 的列作为主列;

b) 为得到可行解, 主行必须选择为

$$\begin{array}{}\text{(18.17)}& \frac{b_p}{a_{pq}}=\underset{\begin{array}{c}1\le i\le m\\ a_{iq}>0\end{array}}{min}\left\{\frac{b_i}{a_{iq}}\right\}.\end{array}$$

如果可行集的极端点不是退化的, 则单纯形法在有穷步之后终止 ((情形 a) 或 (情形 b)).

第 1183 页 18.1.2 中的规范形可以写成单纯形表 (表 18.4(a)). 这个表并不是最优的, 因为目标函数在第 3 列中有正系数. 把第 3 列选定为主列 (也可以考虑第 2 列). 对主列的每一正元计算商 $a_i/a_{iq}$ (实际上只有一个). 这些商示于最后一列之后. 最小商就确定主行.

如果它不是唯一的,则对应于新表的极端点是退化的. 在实施(18.16a) $\sim \left(18.16\mathrm{d}\right)$ 几个步骤之后,就得到表 18.4(b). 这个表确定极端点(0,2,0,1,0,2,8),对应于图 18.4 中的点 $P_7$ . 由于这个新表仍然不是最优的,将 $x_3$ 和 $x_6$ 互换 (表 18.4(c)). 第 3 个表中极端点对应于图 18.4 中的点 $P_6$ . 在作附加变换之后,得到最优表 (表 18.4(d)),其极大点为 ${\underset{―}{x}}^{\ast }=\left(2,2,2,5,0,0,0\right)$ ,对应于点 $P_5$ ,并且目标函数在这里取得最大值 $f\left({\underset{―}{x}}^{\ast }\right)=18$ .

2. 退化情形

如果在单纯形表中无法唯一地选择下一个主元, 则表示新的表有退化极端点. 退化极端点在几何上可以解释为可行解凸多面体的重合顶点. 这样的顶点有几个基. 因此, 在这种情形下可能出现若干步后仍出不来新的顶点, 也可能得到前面已经出现的表格, 从而可能发生无限循环的情形.

在退化的极端点情形下,解决问题的一种可能的办法是对 $b_i$ 加上小扰动 ${\epsilon }^i$ (选择适当的 ${\epsilon }^i>0$ ),使得扰动后的极端点不再退化. 如果用 ${\epsilon }^i=0$ 替换,则从扰动问题的解就可得到退化情形的解.

如果在这种非唯一确定情形下随机选择主列, 则在实际中就可能发生无限循环这种异常情形.

18.1.3.3 初始单纯形表的确定

1. 辅助规划、人工变量

如果在原始约束 (18.1b) 中有等式或带负 $b_i$ 的不等式,则从单纯形法找出可行解并不是容易的事情. 为此, 在这种情形下, 我们从辅助规划开始来生成一个可行解,并把它作为原始问题单纯形法的出发点. 系统 $\mathbf{A}\underset{―}{\mathbf{x}}=\underset{―}{\mathbf{b}}$ 的某些方程乘以(-1) 以便满足条件 $\underset{―}{b}\ge \underset{―}{0}$ . 现在 $A\underset{―}{x}=\underset{―}{b}$ 中的 $\underset{―}{b}\ge \underset{―}{0}$ ,其每一式的左端加上人工变量 $y_k\left(k=1,\cdots ,m\right)$ ,并考虑辅助规划问题:

$$\begin{array}{}\text{(18.18a)}& {\mathbf{OF}}^{\ast }:g\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{y}}\right)=-y_1-\cdots -y_m=max!\end{array}$$$$\begin{array}{}\text{(18.18b)}& \begin{array}{cccc}{a}_{1,1}{x}_1+\cdots +a_{1,n}{x}_n+y_1& =b_1,& & \\ ⋮& ⋮& \ddots & ⋮\\ a_{m,1}{x}_1+\cdots +a_{m,n}{x}_n+& & & +y_m=b_m,\\ x_1,\cdots ,x_n\ge 0;y_1,\cdots ,y_m\ge 0.& & & \end{array}\}\end{array}$$

在这个问题中,变量 $y_1,\cdots ,y_m$ 是基变量,并且可以着手做第 1 张单纯形表 (表 18.5). 这个表的最后一行包含非基变量之和,这些和是新的辅助目标函数 ${\mathbf{OF}}^{\ast }$ 的系数. 显然,总有 $g\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{y}}\right)\le 0$ . 如果对于此辅助规划问题的某个极大点 $\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)$ 有 $g\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)=0$ ,则显然有 ${\underset{―}{\mathbf{y}}}^{\ast }=\underset{―}{\mathbf{0}}$ ,从而 ${\underset{―}{\mathbf{x}}}^{\ast }$ 是 $\mathbf{A}\underset{―}{\mathbf{x}}=\underset{―}{\mathbf{b}}$ 的解. 如果 $g\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)<0$ , 则 $\mathbf{A}\underset{―}{\mathbf{x}}=\underset{―}{\mathbf{b}}$ 无解.

表 18.5

	$x_1$	...	$x_n$
$y_1$	$a_{1,1}$	...	$a_{1,n}$	$b_1$
$⋮$	$⋮$		$⋮$	$⋮$
$y_m$	$a_{m,1}$	...	$a_{m,n}$	$b_m$
OF	$c_1$	...	$c_m$	0
$\mathbf{OF}\ast$		...		$\sum _{j=1}^n{b}_j=-g\left(\underset{―}{\mathbf{0}},\underset{―}{\mathbf{b}}\right)$

2. 辅助规划问题的解

我们的目的是从基中消除人工变量. 下面来准备一个表, 此表不光是为了辅助规划问题. 我们通过人工变量的列和辅助目标函数的行来完成初始表. 辅助目标函数现在包含与等式相关的行所对应的系数之和 (示于下面). 如果人工变量变成了一个非基变量,则其列可以忽略,因为它绝不会再次被选作基变量. 极大点 $\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)$ 一旦被确定, 则要区分两种情形:

(1) $g\left({\underset{―}{x}}^{\ast },{\underset{―}{y}}^{\ast }\right)<0$ : 系统 $A\underset{―}{x}=\underset{―}{b}$ 无解,线性规划问题没有任何可行解.

(2) $g\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)=0$ : 如果基变量中没有人工变量,则这个表就是原问题的初始表. 否则, 通过单纯形法的附加步骤将基变量中所有人工变量消除.

引入人工变量可能会大大增加问题的规模. 并不是每一个方程都有必要引入人工变量. 如果在引入松弛变量和剩余变量 (参见第 1185 页 18.1.2.1,3. 中的注) 之前约束系统的形式是: ${\mathbf{A}}_1\underset{―}{\mathbf{x}}\ge {\underset{―}{\mathbf{b}}}_1,{\mathbf{A}}_2\underset{―}{\mathbf{x}}={\underset{―}{\mathbf{b}}}_2,{\mathbf{A}}_3\underset{―}{\mathbf{x}}\le {\underset{―}{\mathbf{b}}}_3$ ,其中 ${\underset{―}{\mathbf{b}}}_1,{\underset{―}{\mathbf{b}}}_2,{\underset{―}{\mathbf{b}}}_3>\underset{―}{\mathbf{0}}$ ,那么仅仅前两个系统需要引入人工变量, 至于第三个系统, 可以选松弛变量作为基变量. 在第 1184 页 18.1.2 的例子中, 仅第一个方程需要人工变量:

在 $g\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{y}}}^{\ast }\right)=0$ 之下,相应的表 (表 18.6(b)) 是最优的. 在略去第 2 列之后, 就得到原问题的第 1 张表.

	$x_1$	$x_2$	$x_3$	$x_4$
$y_1$	1	$\underset{―}{1}$	$\underset{―}{1}$	-1	1	:
$x_5$	0	1	0	0	2	:
$x_6$	-1	0	2	0	2
$x_7$	2	-3	2	0	2
$\mathbf{OF}$	2	$\underset{―}{3}$	4	0	0
OF*	1	1	1	-1	1

	$x_1$	$y_1$	$x_3$	$x_4$
$x_2$	1	1	1	-1	1
$x_5$	-1	-1	-1	1	1
$x_6$	-1	0	2	0	2
$x_7$	5	3	5	-3	5
OF	-1	-3	1	3	-3
OF*	0	-1	0	0	0

18.1.3.4 修正单纯形法

1. 修正单纯形表

假定线性规划问题由如下规范形给出:

$$\begin{array}{}\text{(18.19a)}& \text{OF :}f\left(\mathbf{x}\right)=c_1{x}_1+\cdots +c_{n-m}{x}_{n-m}+c_0=max\text{!}\end{array}$$$$\begin{array}{}\text{(18.19b)}& \begin{array}{l}\text{ T: }{\alpha }_{1,1}{x}_1+\cdots +{\alpha }_{1,n-m}{x}_{n-m}+x_{n-m+1}={\beta }_1,\end{array}\end{array}$$

显然,系数向量 ${\underset{―}{\alpha }}_{n-m+i}\left(i=1,\cdots ,m\right)$ 是第 $i$ 个单位向量.

为了将其改变成另一个规范形, 从而达到另一个极端点, 只需用相应的基逆矩阵乘方程组 (18.19b). (注意如下事实: 如果 ${\mathbf{A}}_B$ 表示一新的基,则向量 $\underset{―}{\mathbf{x}}$ 的坐标在新的基中可以表示成 ${\mathbf{A}}_B^{-1}\underset{―}{\mathbf{x}}$ . 如果已知新的基逆矩阵,则从最初的表通过简单相乘就可以得到任意列和目标函数.) 单纯形法可以这样修改, 使得在每一步而不用通过新表就能确定基逆. 从每个表中只要计算为找出新的主元所需要的元就够了. 如果变量数远大于约束数 $\left(n>3m\right)$ ,那么修改单纯形法的计算量相当小,并有较好的精度. 修改单纯形表的一般形式示于表 18.7.

表 18.7

	$x_1$	...	$x_{n-m}$	$x_{n-m+1}$	...	$x_n$		$x_q$
$x_1^B$				$a_{1,n-m+1}$	...	$a_{1,n}$	$b_1$	$r_1$
$⋮$				$⋮$		$⋮$	$⋮$	$⋮$
$x_m^B$				$a_{m,n-m+1}$	...	$a_{m,n}$	$b_m$	$r_m$
	$c_1$	...	$c_{n-m}$	$c_{n-m+1}$	...	$c_n$	$-c_0$	$c_q$

表中的符号意义如下:

$x_1^B,\cdots ,x_m^B$ : 现时基变量 (如同在第一步中的 $x_{n-m+1},\cdots ,x_n$ 一样);

$c_1,\cdots ,c_n$ : 目标函数的系数 (与基变量相关的系数为零);

$b_1,\cdots ,b_m$ : 现时规范形的右端;

$c_0$ : 目标函数在极端点 $\left(x_1^B,\cdots ,x_m^B\right)=\left(b_1,\cdots ,b_m\right)$ 的取值; ${\mathbf{A}}^{\ast }=\left(\begin{array}{ccc}{a}_{1,n-m+1}& \cdots & a_{1,n}\\ ⋮& & ⋮\\ a_{m,n-m+1}& \cdots & a_{m,n}\end{array}\right)$ : 现时基逆, ${\mathbf{A}}^{\ast }$ 的列是对应现时规范形的 $x_{n-m+1},\cdots ,x_n$ 的列; $\underset{―}{r}={(r_1,\cdots ,r_m)}^{\mathrm{T}}$ : 现时主列.

2. 修正单纯形的步骤

a) 当系数 $c_j\left(j=1,\cdots ,n\right)$ 中至少有一个是正的,则相应的单纯形表不是最优的. 当某个 $c_q>0$ 时,选择相应的 $q$ 列为主列.

b) 用 ${\mathbf{A}}^{\ast }$ 与原系数矩阵 (18.19b) 的第 $q$ 列相乘,计算出主列 $\underset{―}{r}$ ,并将此新的向量作为表的最后一个列向量. 第 $k$ 个主行向量由类似于单纯形算法 (18.17) 中的方式确定.

c) 新表通过一系列转换步骤 (18.16a $\sim 18.16\mathrm{d}$ ) 算出,这里 $a_{iq}$ 形式上用 $r_i$ 代替, 并且标号限于 $n-m+1\le j\le n$ . 删除列 $\widetilde{\underset{―}{r}},x_q$ 成为基变量. 对于 $j=1,\cdots ,n-m$ , 结果是 ${\tilde{c}}_j=c_j+{\underset{―}{\alpha }}_j^{\mathrm{T}}\underset{―}{\tilde{\mathbf{c}}}$ ,其中 $\underset{―}{\tilde{\mathbf{c}}}={({\tilde{c}}_{n-m+1},\cdots ,{\tilde{c}}_n)}^{\mathrm{T}}$ ,而 ${\alpha }_j$ 是 (18.19b) 的系数矩阵的第 $j$ 列.

考虑第 1184 页 18.1.2 中例子的规范形. 我们希望把 $x_4$ 变成基. 相应的主列 $\underset{―}{r}={\underset{―}{\alpha }}_4$ 放置到表的最后一列 (表 18.8(a))(初始时 ${\mathbf{A}}^{\ast }$ 是单位矩阵).

对于 $j=1,3,4$ ,我们得到 ${\tilde{c}}_j=c_j-3{\alpha }_{2j}:\left(c_1,c_3,c_4\right)=\left(2,4,0\right)$ . 这样确定的极端点 $\underset{―}{x}=\left(0,2,0,1,0,2,8\right)$ 对应于第 1184 页图 18.4 中的点 $P_7$ . 下一个主列可以选在 $j=3=q$ .

	$x_1$	$x_3$	$x_4$	$x_2$	$x_5$	$x_6$	$x_7$		$x_4$
$x_2$				1	0	0	0	1	-1
$x_5$				$\underset{―}{0}$	1	$\underset{―}{0}$	$\underset{―}{0}$	$\underset{―}{1}$	$\underset{―}{\underset{―}{1}}$
$x_6$				0	0	1	0	2	$\underset{―}{0}$
$x_7$				0	0	0	1	5	-3
	-1	1	3	0	0	0	0	-3	$\underset{―}{3}$

	$x_1$	$x_3$	$x_4$	$x_2$	$x_5$	$x_6$	$x_7$		$x_3$
$x_2$				1	1	0	0	2	$\underset{―}{0}$
$x_4$				0	1	0	0	1	-1
$x_6$				$\underset{―}{0}$	$\underset{―}{0}$	$\underset{―}{1}$	0	2	2	2
$x_7$				0	3	0	1	8	2	8
	2	$\underset{―}{4}$	-3	0	-3	0	0	-6	$\underset{―}{4}$

向量 $\underset{―}{r}$ 由

$$\underset{―}{\mathbf{r}}=\left(r_1,\cdots ,r_m\right)={\mathbf{A}}^{\ast }{\underset{―}{\alpha }}_3=\left(\begin{array}{cccc}1& 1& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 3& 0& 1\end{array}\right)\left(\begin{array}{c}1\\ -1\\ 2\\ 5\end{array}\right)=\left(\begin{array}{c}0\\ -1\\ 2\\ 2\end{array}\right)$$

确定, 并将之放到第二个表 (表 18.8(b)) 的最后一列. 用类似于第 1187 页 18.1.3.2 中所示的方法继续做下去. 如果想回到原先的方法, 则非基变量所对应的初始列构成的矩阵必须乘以 ${\mathbf{A}}^{\ast }$ ,并且只保留这些列.

18.1.3.5 线性规划中的对偶性

1. 对应

对于任意一个线性规划问题 (原始问题), 可以指定另一个线性规划问题 (对偶问题):对偶问题

原始问题

$$\begin{array}{}\text{(18.20a)}& \text{OF:}f\left(\underset{―}{\mathbf{x}}\right)={\underset{―}{\mathbf{c}}}_1^{\mathrm{T}}{\underset{―}{\mathbf{x}}}_1+{\underset{―}{\mathbf{c}}}_2^{\mathrm{T}}{\underset{―}{\mathbf{x}}}_2=max\text{!}\end{array}$$$$\text{CT:}{\mathbf{A}}_{1,1}{\underset{―}{\mathbf{x}}}_1+{\mathbf{A}}_{1,2}{\underset{―}{\mathbf{x}}}_2\le {\underset{―}{\mathbf{b}}}_1\text{,}$$$$\begin{array}{}\text{(18.20b)}& {\mathbf{A}}_{2,1}{\underset{―}{\mathbf{x}}}_1+{\mathbf{A}}_{2,2}{\underset{―}{\mathbf{x}}}_2={\underset{―}{\mathbf{b}}}_2,\end{array}$$

${\underset{―}{\mathbf{x}}}_1\ge \underset{―}{\mathbf{0}},{\underset{―}{\mathbf{x}}}_2$ 自由.

对偶问题

$$\begin{array}{}\text{(18.21a)}& {\mathbf{OF}}^{\ast }:g\left(\underset{―}{\mathbf{u}}\right)={\underset{―}{\mathbf{b}}}_1^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_1+{\underset{―}{\mathbf{b}}}_2^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_2=min!\end{array}$$$${\mathbf{CT}}^{\ast }:{\mathbf{A}}_{1,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_1+{\mathbf{A}}_{2,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_2\ge {\underset{―}{\mathbf{c}}}_1,$$$$\begin{array}{}\text{(18.21b)}& {\mathbf{A}}_{1,2}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_1+{\mathbf{A}}_{2,2}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_2={\underset{―}{\mathbf{c}}}_2,\end{array}$$$${\underset{―}{\mathbf{u}}}_1\ge \underset{―}{\mathbf{0}},{\underset{―}{\mathbf{u}}}_2\text{自由.}$$

一个问题的目标函数的系数构成另一个问题约束的右端向量. 每个自由变量对应于一个等式, 而带限制符号的变量则对应于另一个问题的一个不等式.

2. 对偶性定理对偶性定理

a) 如果两个问题都有可行解,即 $M\ne \varnothing ,M^{\ast }\ne \varnothing$ (这里 $M$ 和 $M^{\ast }$ 分别表示原问题和对偶问题的可行集), 那么

$$\begin{array}{}\text{(18.22a)}& f\left(\underset{―}{\mathbf{x}}\right)\le g\left(\underset{―}{\mathbf{u}}\right),\mathrm{\forall }\underset{―}{\mathbf{x}}\in M,\underset{―}{\mathbf{u}}\in M^{\ast },\end{array}$$

并且两个问题都有最优解.

b) 点 $\underset{―}{x}\in M$ 和 $\underset{―}{u}\in M^{\ast }$ 是相应问题的最优解,当且仅当

$$\begin{array}{}\text{(18.22b)}& f\left(\underset{―}{\mathbf{x}}\right)=g\left(\underset{―}{\mathbf{u}}\right).\end{array}$$

c) 如果 $f\left(\underset{―}{x}\right)$ 在 $M$ 上没有上界,或 $g\left(\underset{―}{u}\right)$ 在 $M^{\ast }$ 上没有下界,那么 $M^{\ast }=\varnothing$ 或 $M=\varnothing$ ,即对偶问题没有可行解.

d) 点 $\underset{―}{x}\in M$ 和 $\underset{―}{u}\in M^{\ast }$ 是相应问题的最优点,当且仅当

$$\begin{array}{}\text{(18.22c)}& {\underset{―}{\mathbf{u}}}_1^{\mathrm{T}}\left({\mathbf{A}}_{1,1}{\underset{―}{\mathbf{x}}}_1+{\mathbf{A}}_{1,2}{\underset{―}{\mathbf{x}}}_2-{\underset{―}{\mathbf{b}}}_1\right)=0\text{ 和 }{\underset{―}{\mathbf{x}}}_1^{\mathrm{T}}\left({\mathbf{A}}_{1,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_1+{\mathbf{A}}_{2,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_2-{\underset{―}{\mathbf{c}}}_1\right)=0.\end{array}$$

使用上面最后两个方程,从对偶问题的非降秩最优解 $\underset{―}{u}$ ,通过求解如下线性方程组可以找到原问题的最优解 $\underset{―}{x}$ :

$$\begin{array}{}\text{(18.23a)}& {\mathbf{A}}_{2,1}{\underset{―}{\mathbf{x}}}_1+{\mathbf{A}}_{2,2}{\underset{―}{\mathbf{x}}}_2-{\underset{―}{\mathbf{b}}}_2=\underset{―}{\mathbf{0}},\end{array}$$$$\begin{array}{}\text{(18.23b)}& {({\mathbf{A}}_{1,1}{\underset{―}{\mathbf{x}}}_1+{\mathbf{A}}_{1,2}{\underset{―}{\mathbf{x}}}_2-{\underset{―}{\mathbf{b}}}_1)}_i=\underset{―}{\mathbf{0}}\text{ 当 }{u}_i>0,\end{array}$$$$\begin{array}{}\text{(18.23c)}& x_i=0\text{ 当 }{({\mathbf{A}}_{1,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_1+{\mathbf{A}}_{2,1}^{\mathrm{T}}{\underset{―}{\mathbf{u}}}_2-{\underset{―}{\mathbf{c}}}_1)}_i\ne 0.\end{array}$$

对偶问题也可以用单纯形法进行求解.

3. 对偶问题的应用

在如下情形下, 借助对偶问题求解可能有某些优点:

a) 如果能简单地找出对偶问题的规范形, 则从原问题切换到对偶问题.

b) 如果原问题的约束数量相比变量数大得多, 则可使用修正单纯形法处理对偶问题.

考虑第 1184 页 18.1.2 中例子的原问题.

原问题

$$\text{OF:}f\left(\underset{―}{\mathbf{x}}\right)=2x_1+3x_2+4x_3=max\text{!}$$$$\text{CT:}-x_1-x_2-x_3\le -1\text{,}$$$$x_2\le 2,$$$$-x_1+2x_3\le 2,$$$$2x_1-3x_2+2x_3\le 2,$$$$x_1,x_2,x_3\ge 0.$$

对偶问题

$${\mathbf{OF}}^{\ast }:g\left(\underset{―}{\mathbf{u}}\right)=-u_1+2u_2+2u_3+2u_4=min!$$$$\text{CT*:}-u_1-u_3+2u_4\ge 2\text{,}$$$$-u_1+u_2-3u_4\ge 3,$$$$-u_1+2u_3+2u_4\ge 4,$$$$u_1,u_2,u_3,u_4\ge 0.$$

如果对偶问题是在引入松弛变量后采用单纯形法进行求解,则得到最优解 ${\underset{―}{\mathbf{u}}}^{\ast }=$ $\left(0,7,2/3,4/3\right)$ ,并且 $g\left({\underset{―}{\mathbf{u}}}^{\ast }\right)=18$ . 求解系统 ${(\mathbf{A}\underset{―}{\mathbf{x}}-\underset{―}{\mathbf{b}})}_i=0$ ,这里 $u_i>0$ ,即 $x_2=2,-x_1+2x_3=2,2x_1-3x_2+2x_3=2$ ,得到原问题的解 ${\underset{―}{x}}^{\ast }=\left(2,2,2\right)$ ,$f\left({\underset{―}{x}}^{\ast }\right)=18.$