Appearance
5.8.4 匹配
1. 匹配
图
如果
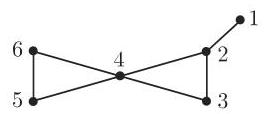
- 在图 5.55 中
是饱和匹配,而 是极大匹配, 并且也是完全匹配.
2. 塔特 (Tutte) 定理
设
完全匹配存在于 (例如) 有偶数个顶点的完全图、完全二部图
3. 交错路
设
4. 贝格 (Berge) 定理
图
如果
- 在图 5.55 中,
是对于匹配 的递增交错路. 如上面所述得到匹配 ,并且 .
5. 极大匹配的确定
设
a) 首先形成一个饱和匹配
b) 选取
c) 如果这样的路存在,那么上面叙述的方法产生一个匹配
有一个埃德蒙兹 (Edmonds) 算法, 是搜索极大匹配的有效方法, 但它的叙述相当复杂 (见 [5.48]).