Appearance
9.1.1 一阶微分方程
9.1.1.1 存在性定理, 方向场
1. 解的存在性
如果函数
在
2. 利普希茨条件
其中
3. 方向场
如果微分方程
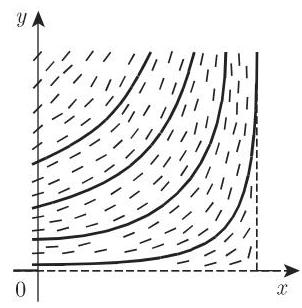
4. 铅垂方向
如果在一个方向场中有一个铅垂方向,即如果函数
在对于微分方程 (9.2) 或 (9.4) 满足存在性条件的区域中,通过每个点
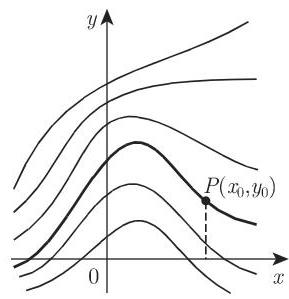
5. 通解
(9.2) 的所有积分曲线的集合可以被一个参数所刻画, 因而它可以由相应的单参数曲线族的方程
给出. 参数
所表示.
9.1.1.2 重要的求解方法
1. 分离变量法
如果一个微分方程可以被变换为如下形式
那么它可以被重写为
其中变量
如果对于某些值
If
2. 齐次方程
如果
中,通过代换
3. 恰当微分方程
一个恰当微分方程 (exact differential equation) 是一个形如
的方程,如果存在两个变量的一个函数
即,如果 (9.9a) 的左端是一个函数
是方程 (9.9a) 成为恰当的一个充要条件. 在此情形, (9.9a) 的通解是函数
它可以根据第 692 页 8.3.4.4 (8.132) 作为积分
而被计算,其中
- 本页 4. 将给出一些例子.
4. 积分因子
一个函数
乘以
这个方程的每个特解是一个积分因子. 得到这个偏微分方程的通解比解原始方程复杂得多,因而人们通常寻找一种特殊形式的解
5. 一阶线性微分方程
一个一阶线性微分方程 (first-order linear differential equation) 有如下形式
其中未知函数
这里是一个积分因子:
而通解是
在这个公式中用下界为
给出. 如果
6. 伯努利微分方程
伯努利 (Bernoulli) 微分方程是形如
的方程,如果它被
- 求解微分方程
. 由于 ,用 除,并引进新变量 , 得到方程 . 利用线性微分方程解的公式,有 和 . 因而,最后得到 .
7. 里卡蒂微分方程
里卡蒂 (Riccati) 微分方程
通常不能用初等积分法求解, 即不能利用有限次的初等积分法求得解. 然而, 有可能通过适当的代换将其变化为一些微分方程, 而这些微分方程可以求得它们的解.
方法 1 由代换
里卡蒂微分方程可以被变化为正规形式 (normal form)
其中
因而, 微分方程中未知函数的一次项就消失了.
如果通过一个适当途径可以发现 (9.13c) 的一个特解
(9.13c)即被变化为
利用 (9.13e) 和 (9.13b), 从 (9.13f) 的解就得到 (9.13a) 的解.
方法 2 由代换
(9.13a) 可以被变化为一个二阶线性微分方程 (参见第 741 页 9.1.2.6, 1.):
方法 1 取
方法 2 根据 (9.13h),得到欧拉微分方程
9.1.1.3 隐式微分方程
1. 参数形式的解
给定一个隐式微分方程
那么通过一个点
a) 在点
b) 函数
如果从原来的方程可以解出
2. 拉格朗日微分方程
拉格朗日 (Lagrange) 微分方程是方程
由上面给出的方法可以确定其解. 如果
则
是(9.15a)的一个奇异解.
3. 克莱罗微分方程
克莱罗 (Clairaut) 微分方程是拉格朗日微分方程的特殊情形, 如果
因而它可以被变化为
其通解为
除了通解外, 克莱罗微分方程还有一个奇异解, 它可以从方程
和
中消去常数
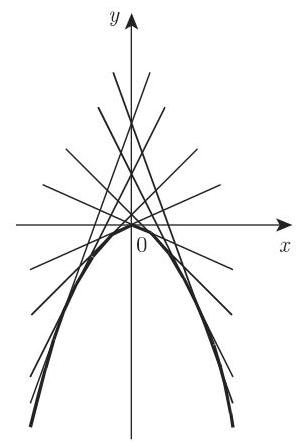
9.1.1.4 奇异积分和奇点
1. 奇异元素
一个元素
外, 它还满足方程
2. 奇异积分
通过奇异元素的积分曲线被称为奇异积分曲线 (singular integral curve); 一条奇异积分曲线的方程
被称为一个奇异积分 (singular integral). 积分曲线的包络是奇异积分曲线 (图 9.3); 它们由奇异元素组成.
在一条奇异积分曲线的点处, 通常缺乏解的唯一性 (参见第 715 页 9.1.1.1, 1.).
3. 奇异积分的确定
通常,对于通解的任意常数的任何值,不能得到奇异积分. 为了确定
并消去
根式 (radicals) 是由嵌套 (nesting) 代数方程 (参见第 79 页 2.2.1) 得到的表达式. 如果已知积分曲线族的方程, 即, 已知所给微分方程的通解, 那么可以用微分几何的方法 (参见第 342 页 3.6.1.7) 确定曲线族的包络 - 奇异积分.
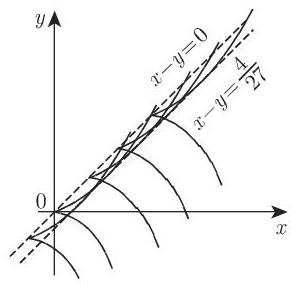
4. 微分方程的奇点
一个微分方程
的奇点是使得该方程右端没有定义的那些点. 例如, 下述形式的微分方程就是这种情形.
(1)具有线性函数分式的微分方程
在(0,0)处有一个孤立奇点 (isolated singular point),因为在几乎所有任意接近
可以使得这些条件被强行满足. 在奇点的邻域中积分曲线的性状依赖于特征方程 (characteristic equation)
的诸根. 可以分类出下述一些情形.
情形 1 如果两个根都是实的, 并且有相同的符号, 那么奇点是一个分支点 (branch point). 奇点邻域中的积分曲线通过奇点, 并且如果特征方程的两个根不相等, 那么除了一条积分曲线外, 它们有公共的切线. 如果两个根相等, 那么或者所有的积分曲线都有相同的切线, 或者存在唯一一条积分曲线在每个方向通过该奇点.
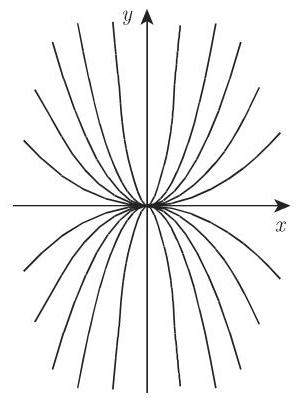
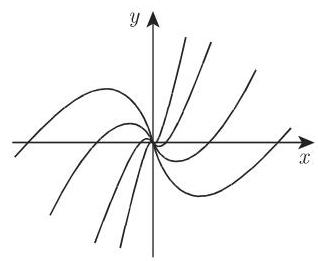
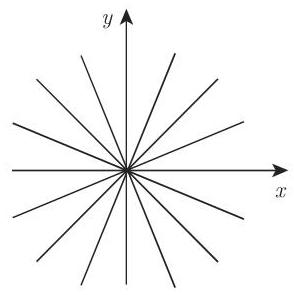
: 对于 ,特征方程是 ,其根为 . 积分曲线是 (图 9.7). 其奇点是所谓的射线点 (ray point).
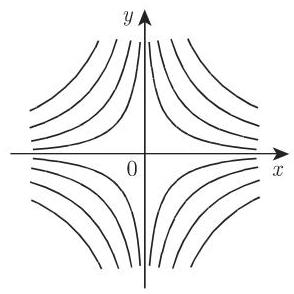
情形 2 如果两个根是实的并且有不同的符号, 则奇点是一个鞍点 (saddle point), 并且两条积分曲线通过它.
情形 3 如果两个根是有非零实部
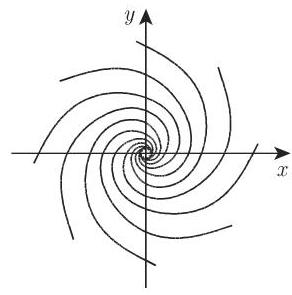
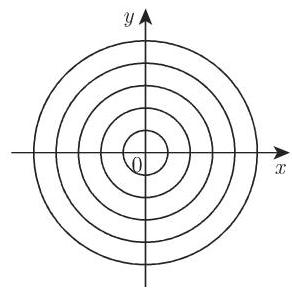
情形 4 如果两个根是纯虚数, 那么奇点是一个中心点 (central point), 或者中心 (center), 闭的积分曲线围绕着它.
: 对于 ,特征方程是 ,其根为 . 积分曲线是 (图 9.10).
(2)具有两个任意函数之比的微分方程
在使得
的点(x, y)处是奇点. 如果
这里
a) 如果近似方程的奇点是一个中心, 那么原始方程的奇点或是中心, 或是焦点.
b) 如果
9.1.1.5 求解一阶微分方程的近似方法
1. 皮卡逐次逼近法
对于
的积分法导致不动点问题
在 (9.20b) 的右端以另一函数
这个皮卡逐次逼近法 (Picard method of successive approximation) 是一种迭代法 (iteration method) (参见第 1233 页 19.1.1).
2. 用级数展开求解
如果已知一个微分方程的解函数在自变量的初始值
给出该方程解的泰勒级数的表达式. 诸导数的值可以通过对原始方程逐次求导, 并代入诸初始条件而确定. 如果原微分方程可以无穷次求导, 那么所得的级数在自变量初始值的某个邻域中收敛. 这个方法也可被用于
注 上面的结果是函数的泰勒级数, 它可能不表示该函数本身 (参见第 630 页 7.3.3.3,1.).
在用一个有未知系数的无穷级数替代解, 并用比较系数来确定这些系数时, 这经常是有用的.
|B: 用下述方法可以解具有相同初始条件的同一个微分方程: 把
3. 微分方程的图解法
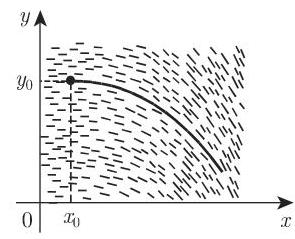
微分方程的图解积分法是基于方向场的一种方法 (参见第 715 页 9.1.1.1, 3.). 在图 9.11 中的积分曲线由一条折线所表示, 它起始于给定的初始点, 由短线段组成. 这些线段的方向总是与线段在起始点处方向场的方向相同. 这也是前一线段的端点.
4. 微分方程的数值解
微分方程的数值解将在 19.4 中详细讨论. 当方程