8.5.2 第二类曲面积分

第二类曲面积分也称为投影积分, 与第一类曲面积分类似, 也是二重积分概念的推广.

8.5.2.1 第二类曲面积分的概念

1. 有向曲面的概念

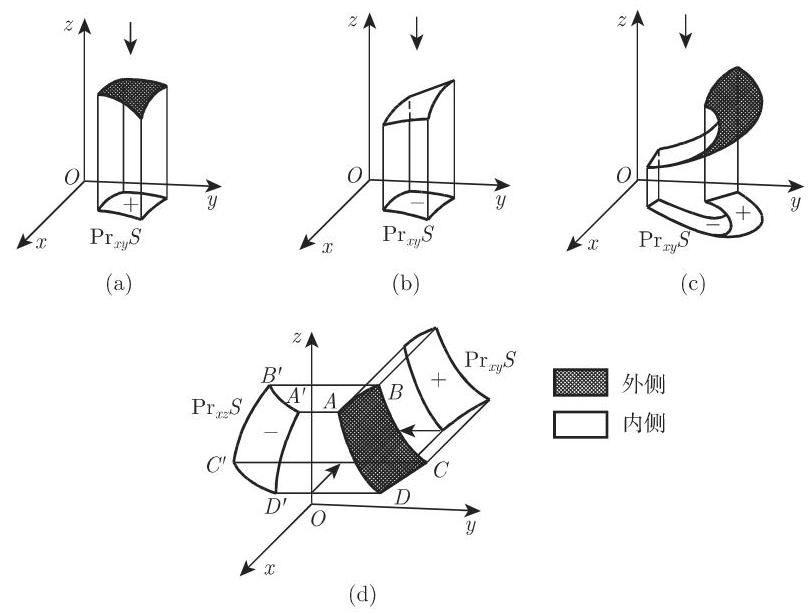
通常曲面有两侧, 可以选择任意一侧作为外侧. 若外侧固定, 则该曲面称为有向曲面. 对于不能定义两侧的曲面, 此处不作讨论 (参见 [8.12]).

2. 有向曲面在坐标面上的投影

将有向曲面上一有界区域 $S$ 向坐标面投影,如向 $xOy$ 面投影,可以按如下方法规定投影 $\underset{xy}{Pr}S$ 的正负 (图 8.46):

a) 若从 $z$ 轴的正向看向 $xOy$ 面时,看到的是曲面 $S$ 的正面 (把外侧作为正面),则射影 $\underset{xy}{Pr}S$ 取正号,否则取负号 (图 8.46(a),(b))

b) 若曲面有一部分是正面,有一部分是反面,则射影 $\underset{xy}{Pr}S$ 可看作正负投影的代数和 (图 8.46(c)).

图 $8.46\left(\mathrm{d}\right)$ 是曲面 $S$ 分别在 $xOz$ 和 $yOz$ 面上的投影 $\underset{xz}{Pr}S$ 和 $\underset{yz}{Pr}S$ ; 符号一正一负.

闭有向曲面的投影等于 0 .

3. 在坐标面上投影的第二类曲面积分的定义

设 $f\left(x,y,z\right)$ 为一个定义在一连通区域上三元函数, $S$ 是函数定义域内的一有向曲面,且 $S$ 上的点与其在 $xOy$ 面上的投影一一对应,则 $f\left(x,y,z\right)$ 的第二类曲面积分定义为 $f\left(x,y,z\right)$ 在该投影的积分

$$\begin{array}{}\text{(8.155)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}x\mathrm{d}y\end{array}$$

与第一类曲面积分的计算方法类似,但在第三步中不用 $f\left(x_i,y_i,z_i\right)$ 乘以小区域的面积 $\mathrm{\Delta }{S}_i$ ,而是用 $f\left(x_i,y_i,z_i\right)$ 乘以第 709 页 8.5.2.1,2. 中规定的 $S$ 在 $xOy$ 面上

的有向投影 $\underset{xy}{Pr}\mathrm{\Delta }{S}_i$ ,于是有

$$\begin{array}{}\text{(8.156a)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}x\mathrm{d}y=\underset{\begin{array}{c}\mathrm{\Delta }{S}_i\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\underset{xy}{Pr}\mathrm{\Delta }{S}_i.\end{array}$$

类似地可定义有向曲面 $S$ 在 $yOz$ 和 $zOx$ 上投影的第二类曲面积分:

$$\begin{array}{}\text{(8.156b)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}y\mathrm{d}z=\underset{\begin{array}{c}\mathrm{\Delta }{S}_i\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\underset{yz}{Pr}\mathrm{\Delta }{S}_i,\end{array}$$$$\begin{array}{}\text{(8.156c)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}z\mathrm{d}x=\underset{\begin{array}{c}\mathrm{\Delta }{S}_i\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\underset{zx}{Pr}\mathrm{\Delta }{S}_i.\end{array}$$

4. 第二类曲面积分存在定理

若函数 $f\left(x,y,z\right)$ 连续,定义曲面的方程也连续且有连续导数,则第二类曲面积分(8.156a,8.156b,8.156c)存在.

8.5.2.2 第二类曲面积分的计算

主要计算方法可化为二重积分的计算.

1. 由显形式给出的曲面

若曲面 $S$ 的显形式方程为

$$\begin{array}{}\text{(8.157)}& z=\phi \left(x,y\right),\end{array}$$

则积分 (8.156a) 可由以下公式来计算

$$\begin{array}{}\text{(8.158a)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}x\mathrm{d}y={\int }_{\underset{xy}{Pr}S}f\left[x,y,\phi \left(x,y\right)\right]\mathrm{d}{S}_{xy},\end{array}$$

其中 $S_{xy}=\underset{xy}{Pr}S$ . 类似地,对曲面 $S$ 在其他坐标面的投影,函数 $f\left(x,y,z\right)$ 的曲

面积分为

$$\begin{array}{}\text{(8.158b)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}y\mathrm{d}z={\int }_{\underset{yz}{Pr}S}f\left(\psi \left(y,z\right),y,z\right)\mathrm{d}{S}_{yz},\end{array}$$

其中曲面方程为 $x=\psi \left(y,z\right)$ ,且 $S_{yz}=\underset{yz}{Pr}S$ .

$$\begin{array}{}\text{(8.158c)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}z\mathrm{d}x={\int }_{\underset{zx}{Pr}S}f\left(x,\chi \left(z,x\right),z\right)\mathrm{d}{S}_{zx},\end{array}$$

其中曲面方程为 $y=\chi \left(z,x\right)$ ,且 $S_{zx}=\underset{zx}{Pr}S$ . 若改变曲面的方向,即把曲面的内外两侧互换, 则投影上的积分换号.

2. 以参数形式给出的曲面

若曲面的参数方程为

$$\begin{array}{}\text{(8.159)}& x=x\left(u,v\right),y=y\left(u,v\right),z=z\left(u,v\right),\end{array}$$

可借助如下公式计算积分(8.156a,8.156b,8.156c):

$$\begin{array}{}\text{(8.160a)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}x\mathrm{d}y={\int }_{\mathrm{\Delta }}f\left[x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right]\frac{D\left(x,y\right)}{D\left(u,v\right)}\mathrm{d}u\mathrm{d}v,\end{array}$$$$\begin{array}{}\text{(8.160b)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}y\mathrm{d}z={\int }_{\mathrm{\Delta }}f\left[x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right]\frac{D\left(y,z\right)}{D\left(u,v\right)}\mathrm{d}u\mathrm{d}v,\end{array}$$$$\begin{array}{}\text{(8.160c)}& {\int }_{S}f\left(x,y,z\right)\mathrm{d}z\mathrm{d}x={\int }_{\mathrm{\Delta }}f\left[x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right]\frac{D\left(z,x\right)}{D\left(u,v\right)}\mathrm{d}u\mathrm{d}v,\end{array}$$

其中表达式 $\frac{D\left(x,y\right)}{D\left(u,v\right)},\frac{D\left(y,z\right)}{D\left(u,v\right)},\frac{D\left(z,x\right)}{D\left(u,v\right)}$ 分别为 $x,y,z$ 中每一函数对关于变量 $u,v$ 的雅可比行列式; $\mathrm{\Delta }$ 为曲面 $S$ 中 $u,v$ 的定义域.