2.17.1 标度

标度的基是一个函数 $y=f\left(x\right)$ ,其目标是从这个函数构造出一个标度,满足在如直线等曲线上,能够把函数值 $y$ 像自变量 $x$ 一样描出来. 标度可看作数表的一维表示形式.

函数 $y=f\left(x\right)$ 标度方程为

$$\begin{array}{}\text{(2.268)}& y=l\left[f\left(x\right)-f\left(x_0\right)\right],\end{array}$$

标度的起点固定在点 $x_0$ . 对一个具体的标度,为了仅有一个给定的标度长度,要考虑标度因子 $l$ .

A 对数标度 当 $l=10\mathrm{cm},x_0=1$ 时,标度方程 $y=10\left[\lg x-\lg 1\right]=10\lg x\left(\mathrm{cm}\right)$ , 由表值

$x$	1	2	3	4	5	6	7	8	9	10
$y=\lg x$	0	0.30	0.48	0.60	0.70	0.78	0.85	0.90	0.95	1

可得到如图 2.95 所示标度.

$◼\mathbf{B}$: 滑尺 从历史看, 滑尺是对数标度中最重要的应用. 例如, 利用两个同样的能沿彼此相互移动的标准对数标度, 可以进行乘法和除法运算.

由表 2.96 可看出: $y_3=y_1+y_2$ ,即 $\lg x_3=\lg x_1+\lg x_2=\lg x_1{x}_2$ ,因此 $x_3=x_1\cdot x_2;y_1=y_3-y_2$ ,即 $\lg x_1=\lg x_3-\lg x_2=\lg \frac{x_3}{x_2}$ ,因此 $x_1=\frac{x_3}{x_2}$ .

$◼\mathbf{C}$: 一圆锥形漏斗的侧面上的体积标度 为了能够读出漏斗内部的体积, 在漏斗上刻有标度. 漏斗的高 $H=15\mathrm{cm}$ ,上面直径 $D=10\mathrm{cm}$ .

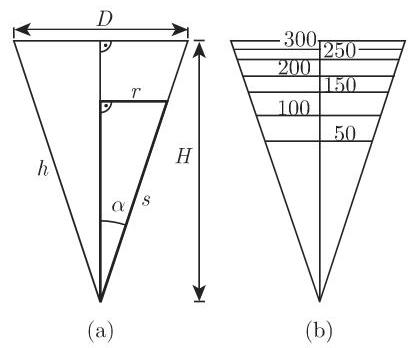
图 2.97(a) 给出的标度方程如下: 体积 $V=\frac{1}{3}{r}^2\pi h$ ,边心距 $s=\sqrt{h^2+r^2}$ , $\tan \alpha =\frac{r}{h}=\frac{D/2}{H}=\frac{1}{3}$ . 由此 $h=3r,s=r\sqrt{10},V=\frac{\pi }{{\left(\sqrt{10}\right)}^3}$ ,故标度方程为 $s=\frac{\sqrt{10}}{\sqrt[3]{\pi }}\sqrt[3]{V}\approx 2.16\sqrt[3]{V}$ . 下表包含了图示中漏斗的标准刻度:

$V$	0	50	100	150	200	250	300	350
$S$	0	7.96	10.03	11.48	12.63	13.61	14.46	15.22