Appearance
17.2.4 维数
17.2.4.1 测度维数
1. 分形
动力系统的吸引子或者其他不变集在几何构造上看可以比点、线或者环面复杂的多. 分形是不依赖于动力系统的集合, 它们依据诸如碎片、多孔性、复杂性和自相似性等一个或几个特征来区分彼此. 通常, 描述光滑曲面或曲线的维数概念不能应用于分形中, 我们需要一个更加一般的维数定义, 关于这方面更多细节可参见 [17.8],[17.20],[17.4].
- 将区间
分成三段长度相等的子区间,去掉三者之中位于中间的开区间后得到集合 . 对 的两个子区间分别进行上述同样操作后, 得到集合 . 继续上述过程,对集合 的所有子区间分别移去中间的三分之一开区间后得到集合 ,如此下去我们得到一列集合 ,其中每个 由 个长度为 的区间组成.
康托尔集
2. 豪斯多夫维数
该维数的定义来自基于勒贝格测度的体积计算. 假设有界集合
设
其中
定义
该值可能有限也可能无穷. 集合
注记 在
豪斯多夫维数的重要性质
(HD1)
(HD2) 如果
(HD3) 如果
(HD4) 如果
(HD5) 如果
(HD6) 设
3. 盒维数或容量
设
称为
称为
若集合
盒维数的重要性质
(BD1)
(BD2) 对
(BD3) 对集合
(BD4) 如果
如果
4. 自相似性
某些具有自相似性质的几何图形可由如下过程得到: 给定一个初始图形, 按比例
对

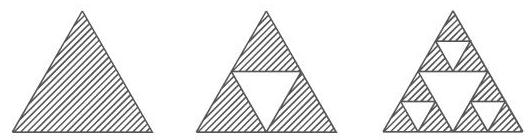
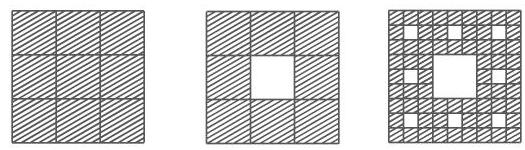
17.2.4.2 由不变测度定义的维数
1. 测度的维数
设
与
分别表示
杨氏 (Young) 定理 1 如果对
称
设
2. 信息维数
设
如果极限
杨氏定理 2 如果对
3. 相关维数
设
称为相关积分,
称为相关维数(如果极限存在).
4. 广义维数
设
称为关于覆盖
如果极限
存在,称其为
特殊情形下的瑞尼维数
**c)
5. 李雅普诺夫维数
设
为测度
如果
列炯皮亚 (Ledrappier) 定理 设
李雅普诺夫维数公式即来自于这一启发式的估计.
|
17.2.4.3 来自杜阿迪和厄斯特勒的局部豪斯多夫维数
设
杜阿迪 (Douady)-厄斯特勒定理 (Desterlé) 设
对微分方程的特别版本 设
为点
对洛伦茨系统 (17.2),当
其中
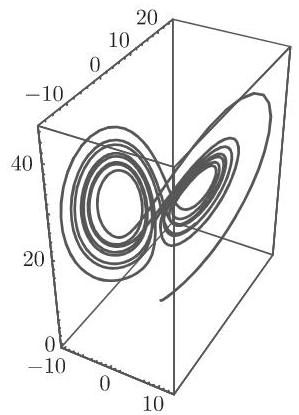
17.2.4.4 吸引子的例子
为关于
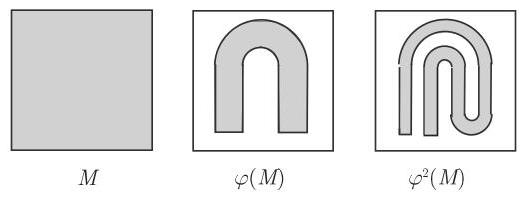
为耗散的面包映射. 图 17.19 给出了面包映射的前两步迭代.
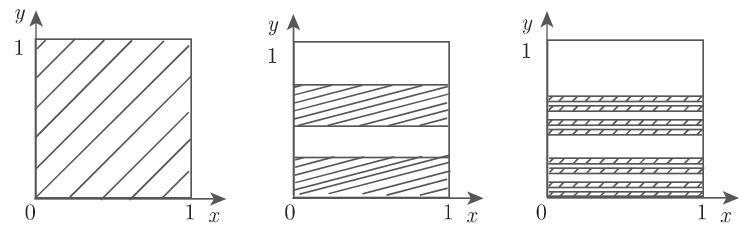
图中可看到 “千层酥” 结构. 集合
对系统
此时测度熵的佩辛熵公式成立, 即
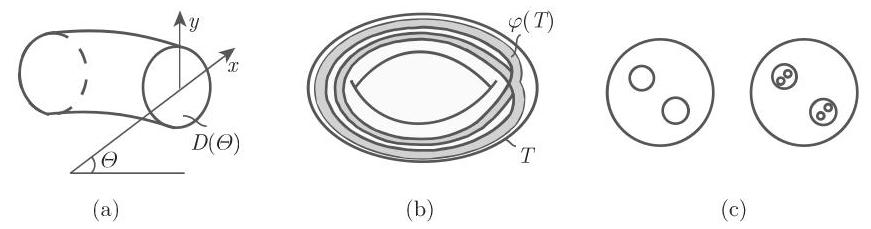
映射
其中