3.4.2 球面三角形的基本性质

3.4.2.1 一般命题

(1)三边之和 三边之和介于 $0^{\circ }$ 和 ${180}^{\circ }$ 之间:

$$\begin{array}{}\text{(3.180)}& 0^{\circ }<a+b+c<{360}^{\circ }.\end{array}$$

(2)两边之和 两边之和大于第三边, 例如

$$\begin{array}{}\text{(3.181)}& a+b>c\text{.}\end{array}$$

(3) 两边之差 两边之差的绝对值小于第三边, 例如

$$\begin{array}{}\text{(3.182)}& \left|a-b\right|<c.\end{array}$$

(4) 三角之和 三角之和介于 ${180}^{\circ }$ 和 ${540}^{\circ }$ 之间:

$$\begin{array}{}\text{(3.183)}& {180}^{\circ }<\alpha +\beta +\gamma <{540}^{\circ }.\end{array}$$

(5) 球面角盈 差

$$\begin{array}{}\text{(3.184)}& ϵ=\alpha +\beta +\gamma -{180}^{\circ }\end{array}$$

称为球面角盈.

(6) 两角之和 两角之和小于第三角增加 ${180}^{\circ }$ ,例如

$$\begin{array}{}\text{(3.185)}& \alpha +\beta <\gamma +{180}^{\circ }.\end{array}$$

(7) 对边和角 较大的边所对的角也较大, 反之亦然.

(8) 面积 球面三角形的面积 $A_{\mathrm{T}}$ 可以用球面角盈 $ϵ$ 和球半径 $R$ 表示成公式

$$\begin{array}{}\text{(3.186a)}& A_{\mathrm{T}}=ϵR^2\cdot \frac{\pi }{{180}^{\circ }}=\frac{R^2ϵ}{\varrho }=R^2\mathrm{arc}ϵ.\end{array}$$

这里 $\varrho$ 是换算因子(3.175c). 用 $A_{\mathrm{S}}$ 表示球的表面积,则根据吉拉尔定理有

$$\begin{array}{}\text{(3.186b)}& A_{\mathrm{T}}=\frac{A_{\mathrm{S}}}{{720}^{\circ }}ϵ.\end{array}$$

如果边是已知的并且不是角盈, 则可借助吕利耶 (L'Huilier) 公式 (3.201) 计算 $ϵ$ .

3.4.2.2 基本公式与应用

本段中所涉及的量的记号与图 3.89 中的那些记号一致.

1. 正弦定律

$$\begin{array}{}\text{(3.187a)}& \frac{\sin a}{\sin b}=\frac{\sin \alpha }{\sin \beta }\end{array}$$$$\begin{array}{}\text{(3.187b)}& \frac{\sin b}{\sin c}=\frac{\sin \beta }{\sin \gamma }\end{array}$$$$\begin{array}{}\text{(3.187c)}& \frac{\sin c}{\sin a}=\frac{\sin \gamma }{\sin \alpha }\end{array}$$

(3.187a) 至 (3.187c) 的等式也可以写成连比的形式, 即球面三角形中边的正弦与所对角的正弦之间的关系:

$$\begin{array}{}\text{(3.187d)}& \frac{\sin a}{\sin \alpha }=\frac{\sin b}{\sin \beta }=\frac{\sin c}{\sin \gamma }.\end{array}$$

球面三角学的正弦定律对应于平面三角学的正弦定律.

2. 余弦定律或关于边的余弦定律

$$\begin{array}{}\text{(3.188a)}& \cos a=\cos b\cos c+\sin b\sin c\cos \alpha ,\end{array}$$$$\begin{array}{}\text{(3.188b)}& \cos b=\cos c\cos a+\sin c\sin a\cos \beta ,\end{array}$$$$\begin{array}{}\text{(3.188c)}& \cos c=\cos a\cos b+\sin a\sin b\cos \gamma .\end{array}$$

球面三角学关于边的余弦定律对应于平面三角学的余弦定律. 我们从记号可以看出余弦定律包含了球面三角学的三条边.

3. 正弦-余弦定律

$$\begin{array}{}\text{(3.189a)}& \sin a\cos \beta =\cos b\sin c-\sin b\cos c\cos \alpha ,\end{array}$$$$\begin{array}{}\text{(3.189b)}& \sin a\cos \gamma =\cos c\sin b-\sin c\cos b\cos \alpha .\end{array}$$

通过量的轮换 (图 3.34), 我们可以再得到四个等式.

正弦-余弦定律对应于平面三角学的投影法则. 因为它包含球面三角形的五个量, 所以并不直接用于解球面三角形问题, 而是用于推导更多的等式.

4. 关于角的余弦定律

$$\begin{array}{}\text{(3.190a)}& \cos \alpha =-\cos \beta \cos \gamma +\sin \beta \sin \gamma \cos a,\end{array}$$$$\begin{array}{}\text{(3.190b)}& \cos \beta =-\cos \gamma \cos \alpha +\sin \gamma \sin \alpha \cos b,\end{array}$$$$\begin{array}{}\text{(3.190c)}& \cos \gamma =-\cos \alpha \cos \beta +\sin \alpha \sin \beta \cos c.\end{array}$$

这个余弦定律的每一种情形包含球面三角形的三个角和一条边. 借助这个定律可以很容易地将一个角用它的对边和夹对边的角来表示, 或者用角表示边; 因此每条边都可以用角来表示. 相比之下,对于平面三角形来说第三个角是从 ${180}^{\circ }$ 内角和计算得出的.

评论 平面三角形的任何一条边都不可能由角来确定, 因为存在着无穷多相似三角形.

5. 对偶正弦-余弦定律

$$\begin{array}{}\text{(3.191a)}& \sin \alpha \cos b=\cos \beta \sin \gamma +\sin \beta \cos \gamma \cos a,\end{array}$$$$\begin{array}{}\text{(3.191b)}& \sin \alpha \cos c=\cos \gamma \sin \beta +\sin \gamma \cos \beta \cos a.\end{array}$$

可以通过量的轮换 (图 3.34) 得到其余四个等式.

正如正弦-余弦定律一样, 对偶正弦-余弦定律通常也不直接用于球面三角形的计算, 而是用于推导更多的公式.

6. 半角公式

为了用球面三角形的边确定它的一个角, 我们可以使用关于边的余弦定律. 半角公式则可以让我们通过角的正切来计算它们, 这类似于平面三角学的半角公式:

$$\begin{array}{}\text{(3.192a)}& \tan \frac{\alpha }{2}=\sqrt{\frac{\sin \left(s-b\right)\sin \left(s-c\right)}{\sin s\sin \left(s-a\right)}},\end{array}$$$$\begin{array}{}\text{(3.192b)}& \tan \frac{\beta }{2}=\sqrt{\frac{\sin \left(s-c\right)\sin \left(s-a\right)}{\sin s\sin \left(s-b\right)}},\end{array}$$$$\begin{array}{}\text{(3.192c)}& \tan \frac{\gamma }{2}=\sqrt{\frac{\sin \left(s-a\right)\sin \left(s-b\right)}{\sin s\sin \left(s-c\right)}},\end{array}$$$$\begin{array}{}\text{(3.192d)}& s=\frac{a+b+c}{2}.\end{array}$$

如果要从球面三角形的三条边确定全部三个角, 那么以下计算是有用的:

$$\begin{array}{}\text{(3.193a)}& \tan \frac{\alpha }{2}=\frac{k}{\sin \left(s-a\right)},\end{array}$$$$\begin{array}{}\text{(3.193b)}& \tan \frac{\beta }{2}=\frac{k}{\sin \left(s-b\right)},\end{array}$$$$\begin{array}{}\text{(3.193c)}& \tan \frac{\gamma }{2}=\frac{k}{\sin \left(s-c\right)},\end{array}$$$$\begin{array}{}\text{(3.193d)}& k=\sqrt{\frac{\sin \left(s-a\right)\sin \left(s-b\right)\sin \left(s-c\right)}{\sin s}},\end{array}$$$$\begin{array}{}\text{(3.193e)}& s=\frac{a+b+c}{2}.\end{array}$$

7. 半边公式

使用半边公式可以从球面三角形的三个角确定它的一条边或全部三条边.

$$\begin{array}{}\text{(3.194a)}& \cot \frac{a}{2}=\sqrt{\frac{\cos \left(\sigma -\beta \right)\cos \left(\sigma -\gamma \right)}{-\cos \sigma \cos \left(\sigma -\alpha \right)}},\end{array}$$$$\begin{array}{}\text{(3.194b)}& \cot \frac{b}{2}=\sqrt{\frac{\cos \left(\sigma -\gamma \right)\cos \left(\sigma -\alpha \right)}{-\cos \sigma \cos \left(\sigma -\beta \right)}},\end{array}$$$$\begin{array}{}\text{(3.194c)}& \cot \frac{c}{2}=\sqrt{\frac{\cos \left(\sigma -\alpha \right)\cos \left(\sigma -\beta \right)}{-\cos \sigma \cos \left(\sigma -\gamma \right)}},\end{array}$$$$\begin{array}{}\text{(3.194d)}& \sigma =\frac{\alpha +\beta +\gamma }{2}\end{array}$$

或

$$\begin{array}{}\text{(3.195a)}& \cot \frac{a}{2}=\frac{k^{\prime }}{\cos \left(\sigma -\alpha \right)},\end{array}$$$$\begin{array}{}\text{(3.195b)}& \cot \frac{b}{2}=\frac{k^{\prime }}{\cos \left(\sigma -\beta \right)},\end{array}$$$$\begin{array}{}\text{(3.195c)}& \cot \frac{c}{2}=\frac{k^{\prime }}{\cos \left(\sigma -\gamma \right)}\end{array}$$

其中

$$\begin{array}{}\text{(3.195d)}& k^{\prime }=\sqrt{\frac{\cos \left(\sigma -\alpha \right)\cos \left(\sigma -\beta \right)\cos \left(\sigma -\gamma \right)}{-\cos \sigma }},\end{array}$$$$\begin{array}{}\text{(3.195e)}& \sigma =\frac{\alpha +\beta +\gamma }{2}.\end{array}$$

因为根据 (3.183), 对于球面三角形的三内角之和有

$$\begin{array}{}\text{(3.196)}& {180}^{\circ }<2\sigma <{540}^{\circ }\text{ 或 }{90}^{\circ }<\sigma <{270}^{\circ }\end{array}$$

成立,所以总有 $\cos \sigma <0$ 一定为真. 鉴于对欧拉三角形的要求,所有的根都是实数.

8. 球面几何基本公式的应用

借助已知的基本公式, 例如距离公式, 可以确定地球上的方位角和航向角. A: 确定德累斯顿 (Dresden) $\left({\lambda }_1={13}^{\circ }{46}^{\prime },{\phi }_1={51}^{\circ }{16}^{\prime }\right)$ 与阿拉木图 (Alma Ata) $\left({\lambda }_2={76}^{\circ }{55}^{\prime },{\phi }_2={43}^{\circ }{18}^{\prime }\right)$ 之间的最短距离.

解 地理坐标 $\left({\lambda }_1,{\phi }_1\right),\left({\lambda }_2,{\phi }_2\right)$ 和北极 $N$ (图 3.94) 为三角形 $P_1{P}_{2}N$ 提供了位于子午线上的两条边 $a={90}^{\circ }-{\phi }_2$ 和 $b={90}^{\circ }-{\phi }_1$ 以及它们之间的夹角 $\gamma ={\lambda }_2-$ ${\lambda }_1$ . 因 $c=e$ ,由余弦定律(3.188c)

$$\cos c=\cos a\cos b+\sin a\sin b\cos \gamma$$

得

$$\cos e=\cos \left({90}^{\circ }-{\phi }_1\right)\cos \left({90}^{\circ }-{\phi }_2\right)+\sin \left({90}^{\circ }-{\phi }_1\right)\sin \left({90}^{\circ }-{\phi }_2\right)\cos \left({\lambda }_2-{\lambda }_1\right)$$$$\begin{array}{}\text{(3.197)}& =\sin {\phi }_1\sin {\phi }_2+\cos {\phi }_1\cos {\phi }_2\cos \left({\lambda }_2-{\lambda }_1\right),\end{array}$$

即 $\cos e=0.53498+0.20567=0.74065,e={42.213}^{\circ }$ . 应用(3.175a)得大圆弧段 $\stackrel{⏜}{P_1{P}_2}$ 的长为 $4694\mathrm{km}$ .

$◼\mathbf{B}$: 计算出发和到达时的航向角 ${\delta }_1$ 和 ${\delta }_2$ ,以及从孟买 $\left({\lambda }_1={72}^{\circ }{48}^{\prime },{\phi }_1={19}^{\circ }{00}^{\prime }\right)$ 到达累斯萨拉姆 $\left({\lambda }_2={39}^{\circ }{28}^{\prime },{\phi }_2=-6^{\circ }{49}^{\prime }\right)$ 沿大圆的航程 (以海里 (n mile) 计).

解 在球面三角形 $P_1{P}_{2}N$ 中借助地理坐标 $\left({\lambda }_1,{\phi }_1\right),\left({\lambda }_2,{\phi }_2\right)$ (图 3.95) 计算两边 $a={90}^{\circ }-{\phi }_1={71}^{\circ }{00}^{\prime },b={90}^{\circ }-{\phi }_2={96}^{\circ }{49}^{\prime }$ 和它们之间的夹角 $\gamma ={\lambda }_1-{\lambda }_2$ $={33}^{\circ }{20}^{\prime }$ . 再由余弦定律 $\left(3.188\mathrm{c}\right)\cos c=\cos e=\cos a\cos b+\sin a\sin b\cos \gamma$ 得 $\stackrel{⏜}{P_1{P}_2}=e={41.777}^{\circ }$ . 因为 $1^{\prime }\approx 1\mathrm{n}$ mile,推得 $\stackrel{⏜}{P_1{P}_2}\approx 2507\mathrm{n}$ mile.

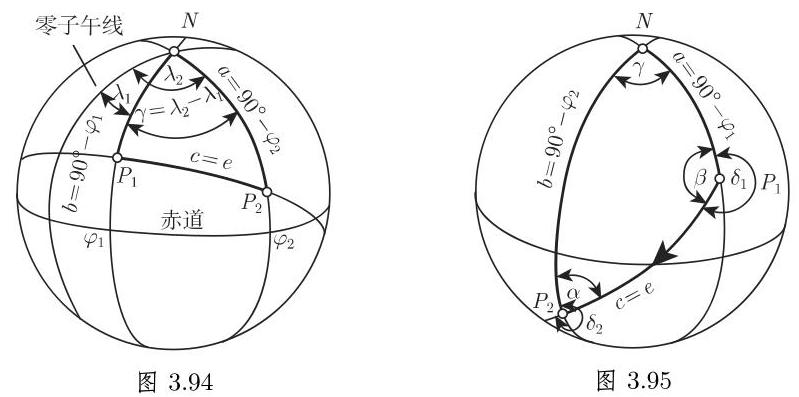
利用关于边的余弦定律 (3.188a) 得

$\alpha =\arccos \frac{\cos a-\cos b\cos c}{\sin b\sin c}={51.248}^{\circ }$ 和 $\beta =\arccos \frac{\cos b-\cos a\cos c}{\sin a\sin c}$

$={125.018}^{\circ }$ .

因此, 结果是

$${\delta }_1={360}^{\circ }-\beta ={234.982}^{\circ }\text{ 和 }{\delta }_2={180}^{\circ }+\alpha ={231.248}^{\circ }.$$

评论 只有当问题中的角明显是锐角或钝角时应用正弦定律确定边和角才有意义.

3.4.2.3 更多的公式

1. 德朗布尔 (Delambre) 等式

类似于平面三角学中的莫尔韦德公式, 对于球面三角形相应的德朗布尔公式成立:

$$\begin{array}{}\text{(3.198a)}& \frac{\cos \frac{\alpha -\beta }{2}}{\sin \frac{\gamma }{2}}=\frac{\sin \frac{a+b}{2}}{\sin \frac{c}{2}},\end{array}$$$$\begin{array}{}\text{(3.198b)}& \frac{\sin \frac{\alpha -\beta }{2}}{\cos \frac{\gamma }{2}}=\frac{\sin \frac{a-b}{2}}{\sin \frac{c}{2}}\end{array}$$$$\begin{array}{}\text{(3.198c)}& \frac{\cos \frac{\alpha +\beta }{2}}{\sin \frac{\gamma }{2}}=\frac{\cos \frac{a+b}{2}}{\cos \frac{c}{2}},\end{array}$$$$\begin{array}{}\text{(3.198d)}& \frac{\sin \frac{\alpha +\beta }{2}}{\cos \frac{\gamma }{2}}=\frac{\cos \frac{a-b}{2}}{\cos \frac{c}{2}}.\end{array}$$

因为对每个等式来说通过轮换还可以再得到两个等式, 所以共有 12 个德朗布尔等式.

2. 纳皮尔 (Neper) 等式和正切定律

$$\begin{array}{}\text{(3.199a)}& \tan \frac{\alpha -\beta }{2}=\frac{\sin \frac{a-b}{2}}{\sin \frac{a+b}{2}}\cot \frac{\gamma }{2},\end{array}$$$$\begin{array}{}\text{(3.199b)}& \tan \frac{\alpha +\beta }{2}=\frac{\cos \frac{a-b}{2}}{\cos \frac{a+b}{2}}\cot \frac{\gamma }{2},\end{array}$$$$\begin{array}{}\text{(3.199c)}& \tan \frac{a-b}{2}=\frac{\sin \frac{\alpha -\beta }{2}}{\sin \frac{\alpha +\beta }{2}}\tan \frac{c}{2},\end{array}$$$$\begin{array}{}\text{(3.199d)}& \tan \frac{a+b}{2}=\frac{\cos \frac{\alpha -\beta }{2}}{\cos \frac{\alpha +\beta }{2}}\tan \frac{c}{2}.\end{array}$$

这些等式也称为纳皮尔类比. 从这些公式可以推出与平面三角学中正切定律类似的公式:

$$\begin{array}{}\text{(3.200a)}& \frac{\tan \frac{a-b}{2}}{\tan \frac{a+b}{2}}=\frac{\tan \frac{\alpha -\beta }{2}}{\tan \frac{\alpha +\beta }{2}},\end{array}$$$$\begin{array}{}\text{(3.200b)}& \frac{\tan \frac{b-c}{2}}{\tan \frac{b+c}{2}}=\frac{\tan \frac{\beta -\gamma }{2}}{\tan \frac{\beta +\gamma }{2}},\end{array}$$$$\begin{array}{}\text{(3.200c)}& \frac{\tan \frac{c-a}{2}}{\tan \frac{c+a}{2}}=\frac{\tan \frac{\gamma -\alpha }{2}}{\tan \frac{\gamma +\alpha }{2}}.\end{array}$$

3. 吕利耶等式

球面三角形的面积可以从已知角 $\alpha ,\beta ,\gamma$ 出发,或者,假如三边 $a,b,c$ 已知,则通过公式 (3.193a) $\sim$ (3.193e) 求出角, 然后根据 (3.184) 借助球面角盈来计算 (3.186a). 吕利耶等式则可以从边出发直接计算角盈 $ϵ$ :

$$\begin{array}{}\text{(3.201)}& \tan \frac{ϵ}{4}=\sqrt{\tan \frac{s}{2}\tan \frac{s-a}{2}\tan \frac{s-b}{2}\tan \frac{s-c}{2}}.\end{array}$$

这个等式对应于平面三角学中的海伦公式.