13.2.5 向量场的旋度

13.2.5.1 旋度的定义

1. 定义

一个向量场 $\overrightarrow{V}$ 在点 $\overrightarrow{r}$ 处的旋度 (rotation 或 curl) 是用 $\mathrm{rot}\overrightarrow{V},\mathrm{curl}\overrightarrow{V}$ ,或用梯度算子 $\mathrm{\nabla }\times \overrightarrow{V}$ 表示的一个向量,并被定义为该向量场的负空间导数:

$$\begin{array}{}\text{(13.57)}& \mathrm{rot}\overrightarrow{V}=-\underset{V\to 0}{lim}\frac{{\text{oiint}}_{\sum }\overrightarrow{V}\times \mathrm{d}\overrightarrow{S}}{V}=\underset{V\to 0}{lim}\frac{{\text{oiint}}_{\sum }\mathrm{d}\overrightarrow{S}\times \overrightarrow{V}}{V}.\end{array}$$

2. 定义

可以用如下方式定义向量场 $\overrightarrow{V}\left(\overrightarrow{r}\right)$ 的旋度向量场:

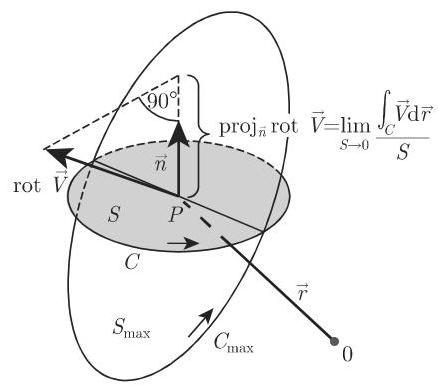
a) 通过点 $\overrightarrow{r}$ 放置一小片曲面 $S$ (图 13.12),并用向量 $\overrightarrow{S}$ 来描述该曲面片,其方向是曲面的法向 $\overrightarrow{n}$ ,其绝对值等于该曲面片的面积. 该曲面的边界用 $C$ 表示.

b) 沿曲线 $C$ (在从曲面的法向看曲线是正定向的意义上)(图 13.12) 计算积分${\oint }_C\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{r}$

c) 在曲面片位置不变时确定极限 (如果存在的话) $\underset{S\to 0}{lim}\frac{1}{S}{\oint }_C\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{r}$ .

d) 为了得到极限的最大值,改变曲面片的位置. 在这个位置曲面面积是 $S_{max}$ , 相应的边界曲线是 $C_{max}$ .

e) 在点 $\overrightarrow{r}$ 处确定向量 $\mathrm{rot}\overrightarrow{V}$ ,其绝对值等于上面发现的最大值,其方向与相应的曲面的法线方向一致. 因而得到

$$\begin{array}{}\text{(13.58a)}& \left|\mathrm{rot}\overrightarrow{V}\right|=\underset{S_{max}\to 0}{lim}\frac{{\oint }_{C_{max}}\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{r}}{S_{max}}.\end{array}$$

$\mathrm{rot}\overrightarrow{V}$ 在面积为 $S$ 的一曲面的法向上的投影,即向量 $\mathrm{rot}\overrightarrow{V}$ 在任一方向 $\overrightarrow{n}=\overrightarrow{l}$ 上的

分量为

$$\begin{array}{}\text{(13.58b)}& \overrightarrow{l}\cdot \mathrm{rot}\overrightarrow{V}={\mathrm{rot}}_l\overrightarrow{V}=\underset{S\to 0}{lim}\frac{{\oint }_C\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{r}}{S}.\end{array}$$

向量场 $\mathrm{rot}\overrightarrow{V}$ 的向量线被称为向量场 $\overrightarrow{V}$ 的旋度线 (curl lines of the vector field $\overrightarrow{V}$ ).

13.2.5.2 不同坐标系中的旋度

1. 笛卡儿坐标系中的旋度

$$\mathrm{rot}\overrightarrow{V}=\overrightarrow{i}\left(\frac{\partial V_z}{\partial y}-\frac{\partial V_y}{\partial z}\right)+\overrightarrow{j}\left(\frac{\partial V_x}{\partial z}-\frac{\partial V_z}{\partial x}\right)+\overrightarrow{k}\left(\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y}\right)$$$$\begin{array}{}\text{(13.59a)}& =\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ V_x& V_y& V_z\end{array}\right|\end{array}$$

向量场 $\mathrm{rot}\overrightarrow{V}$ 可以被表示为梯度算子 $\mathrm{\nabla }$ 和向量 $\overrightarrow{V}$ 的向量积:

$$\begin{array}{}\text{(13.59b)}& \mathrm{rot}\overrightarrow{V}=\mathrm{\nabla }\times \overrightarrow{V}\end{array}$$

2. 柱面坐标系中的旋度

$$\begin{array}{}\text{(13.60a)}& \mathrm{rot}\overrightarrow{V}={\mathrm{rot}}_{\rho }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\rho }+{\mathrm{rot}}_{\phi }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\phi }+{\mathrm{rot}}_z\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_z,\end{array}$$

其中

$${\mathrm{rot}}_{\rho }\overrightarrow{V}=\frac{1}{\rho }\frac{\partial V_z}{\partial \phi }-\frac{\partial V_{\phi }}{\partial z},{\mathrm{rot}}_{\phi }\overrightarrow{V}=\frac{\partial V_{\rho }}{\partial z}-\frac{\partial V_z}{\partial \rho },{\mathrm{rot}}_z\overrightarrow{V}=\frac{1}{\rho }\left\{\frac{\partial }{\partial \rho }\left(\rho V_{\phi }\right)-\frac{\partial V_{\rho }}{\partial \phi }\right\}.$$

(13.60b)

3. 球面坐标系中的旋度

$$\begin{array}{}\text{(13.61a)}& \mathrm{rot}\overrightarrow{V}={\mathrm{rot}}_r\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_r+{\mathrm{rot}}_{\vartheta }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\vartheta }+{\mathrm{rot}}_{\phi }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\phi },\end{array}$$

其中

$${\mathrm{rot}}_r\overrightarrow{V}=\frac{1}{r\sin \vartheta }\left\{\frac{\partial }{\partial \vartheta }\left(\sin \vartheta V_{\phi }\right)-\frac{\partial V_{\vartheta }}{\partial \phi }\right\},$$$$\begin{array}{}\text{(13.61b)}& {\mathrm{rot}}_{\vartheta }\overrightarrow{V}=\frac{1}{r\sin \vartheta }\frac{\partial V_r}{\partial \phi }-\frac{1}{r}\frac{\partial }{\partial r}\left(r{V}_{\phi }\right),\end{array}$$$${\mathrm{rot}}_{\phi }\overrightarrow{V}=\frac{1}{r}\left\{\frac{\partial }{\partial r}\left(r{V}_{\vartheta }\right)-\frac{\partial V_r}{\partial \vartheta }\right\}.$$

4. 一般直角坐标系中的旋度

$$\begin{array}{}\text{(13.62a)}& \mathrm{rot}\overrightarrow{V}={\mathrm{rot}}_{\xi }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\xi }+{\mathrm{rot}}_{\eta }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\eta }+{\mathrm{rot}}_{\zeta }\overrightarrow{V}{\overrightarrow{\mathrm{e}}}_{\zeta },\end{array}$$

其中

$$\begin{array}{}\text{(13.62b)}& \{\begin{array}{l}{\mathrm{rot}}_{\xi }\overrightarrow{V}=\frac{1}{D}\left|\frac{\partial \overrightarrow{r}}{\partial \xi }\right|\left[\frac{\partial }{\partial \eta }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \zeta }\right|V_{\zeta }\right)-\frac{\partial }{\partial \zeta }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \eta }\right|V_{\eta }\right)\right],\\ {\mathrm{rot}}_{\eta }\overrightarrow{V}=\frac{1}{D}\left|\frac{\partial \overrightarrow{r}}{\partial \eta }\right|\left[\frac{\partial }{\partial \zeta }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \xi }\right|V_{\xi }\right)-\frac{\partial }{\partial \xi }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \zeta }\right|V_{\zeta }\right)\right],\\ {\mathrm{rot}}_{\zeta }\overrightarrow{V}=\frac{1}{D}\left|\frac{\partial \overrightarrow{r}}{\partial \zeta }\right|\left[\frac{\partial }{\partial \xi }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \eta }\right|V_{\eta }\right)-\frac{\partial }{\partial \eta }\left(\left|\frac{\partial \overrightarrow{r}}{\partial \xi }\right|V_{\xi }\right)\right].\end{array}\end{array}$$$$\begin{array}{}\text{(13.62c)}& \overrightarrow{r}\left(\xi ,\eta ,\zeta \right)=x\left(\xi ,\eta ,\zeta \right)\overrightarrow{i}+\left(\xi ,\eta ,\zeta \right)\overrightarrow{j}+\left(\xi ,\eta ,\zeta \right)\overrightarrow{k};D=\left|\frac{\partial \overrightarrow{r}}{\partial \xi }\right|\cdot \left|\frac{\partial \overrightarrow{r}}{\partial \eta }\right|\cdot \left|\frac{\partial \overrightarrow{r}}{\partial \zeta }\right|.\end{array}$$

13.2.5.3 旋度的运算法则

$$\begin{array}{}\text{(13.63)}& \mathrm{rot}\left({\overrightarrow{V}}_1+{\overrightarrow{V}}_2\right)=\mathrm{rot}{\overrightarrow{V}}_1+\mathrm{rot}{\overrightarrow{V}}_2,\mathrm{rot}\left(c\overrightarrow{V}\right)=c\mathrm{rot}\overrightarrow{V}.\end{array}$$$$\begin{array}{}\text{(13.64)}& \mathrm{rot}\left(U\overrightarrow{V}\right)=U\mathrm{rot}\overrightarrow{V}+\mathrm{grad}U\times \overrightarrow{V}.\end{array}$$$$\begin{array}{}\text{(13.65)}& \mathrm{rot}\left({\overrightarrow{V}}_1\times {\overrightarrow{V}}_2\right)=\left({\overrightarrow{V}}_2\cdot \mathrm{grad}\right){\overrightarrow{V}}_1-\left({\overrightarrow{V}}_1\cdot \mathrm{grad}\right){\overrightarrow{V}}_2+{\overrightarrow{V}}_1\mathrm{div}{\overrightarrow{V}}_2-{\overrightarrow{V}}_2\mathrm{div}{\overrightarrow{V}}_1\text{.}\end{array}$$

13.2.5.4 位势场的旋度

从斯托克斯 (Stokes) 定理 (参见第 946 页 13.3.3.2) 也可以得到一个位势场的旋度场恒为零:

$$\begin{array}{}\text{(13.66)}& \mathrm{rot}\overrightarrow{V}=\mathrm{rot}\left(\mathrm{grad}U\right)=\overrightarrow{0}.\end{array}$$

如果施瓦茨 (Schwarz) 互换定理的假设条件被满足 (参见第 602 页 6.2.2.2, 1.), 则从 (13.59a) 即得上式对于 $\overrightarrow{V}=\mathrm{grad}U$ 也成立.

$◼$ 对于满足 $r=\left|\overrightarrow{r}\right|=\sqrt{x^2+y^2+z^2}$ 的 $\overrightarrow{r}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$ ,成立下列等式: $\mathrm{rot}\overrightarrow{r}=\overrightarrow{0}$ , 以及 $\mathrm{rot}\left(\phi \left(r\right)\overrightarrow{r}\right)=\overrightarrow{0}$ ,其中 $\phi \left(r\right)$ 是 $r$ 的可微函数.