17.1.4 结构稳定性

17.1.4.1 结构稳定的微分方程

1. 定义

微分方程 (17.1),即向量场 $f:M\to {\mathbb{R}}^n$ 称为结构稳定的,若 $f$ 的小扰动系统与原系统拓扑等价. 严格的定义结构稳定性需要 $M$ 上两个向量场之间距离的概念. 下面我们将研究限定在 $M$ 中的光滑向量场,它们有一个公共的连通吸收开集 $U\subset M$ . 令 $U$ 的边界 $\partial U$ 是光滑的 $n-1$ 维超曲面,并且假设有表示 $\partial U=\left\{x\in {\mathbb{R}}^n:h\left(x\right)=0\right\}$ ,其中 $h:{\mathbb{R}}^n\to \mathbb{R}$ 是 $C^1$ 函数满足在 $\partial U$ 的某个邻域上有 $\mathrm{gradh}\left(x\right)\ne 0$ . 令 $X^1\left(U\right)$ 是 $M$ 上全体光滑向量场构成的度量空间,装配的度量为

$$\begin{array}{}\text{(17.25)}& \rho \left(f,g\right)=\underset{x\in U}{sup}\parallel f\left(x\right)-g\left(x\right)\parallel +\underset{x\in U}{sup}\parallel Df\left(x\right)-Dg\left(x\right)\parallel \end{array}$$

(右端项中第一个 $\parallel \cdot \parallel$ 表示向量的欧几里得范数,第二个 $\parallel \cdot \parallel$ 表示算子范数). 沿 $U$ 方向与边界 $\partial U$ 横截相交的光滑向量场 $f$ ,即满足 $\mathrm{gradh}{\left(x\right)}^{T}f\left(x\right)\ne 0,\left(x\in \partial U\right)$ 且 ${\phi }^t\left(x\right)\in U\left(x\in \partial U,t>0\right)$ ,构成集合 $X_{+}^1\left(U\right)\subset X^1\left(U\right)$ . 向量场 $f\in X_{+}^1\left(U\right)$ 称为结构稳定的,如果存在 $\delta >0$ 使得任意满足 $\rho \left(f,g\right)<\delta$ 的向量场 $g\in X_{+}^1\left(U\right)$ 与 $f$ 是拓扑等价的. 1 考虑平面微分方程 $g\left(\cdot ,\alpha \right)$

$$\begin{array}{}\text{(17.26)}& \dot{x}=-y+x\left(\alpha -x^2-y^2\right),\dot{y}=x+y\left(\alpha -x^2-y^2\right),\end{array}$$

其中,参数 $\alpha$ 满足 $\left|\alpha \right|<1$ . 微分方程 $g$ 属于 $X_{+}^1\left(U\right)$ ,其中 $U=\{\left(x,y\right):x^2+y^2<$ $2\}$ (图 17.12(a)). 显然, $\rho \left(g\left(\cdot ,0\right),g\left(\cdot ,\alpha \right)\right)=\left|\alpha \left(\sqrt{2}+1\right)\right|$ . 向量场 $g\left(\cdot ,0\right)$ 是结构不稳定的. 考虑方程 (17.26) 在极坐标下表示 $\dot{r}=-r^3+\alpha r,\dot{v}=1$ . 显而易见,存在任意靠近 $g\left(\cdot ,0\right)$ 的向量场与 $g\left(\cdot ,0\right)$ 不是拓扑等价的 (图 17.12(b),(c)). 当 $\alpha >0$ 时, 存在稳定的极限环 $r=\sqrt{\alpha }$ .

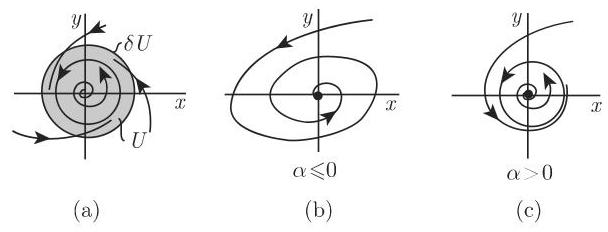
2. 平面上的结构稳定系统

假设 $f\in X_{+}^1\left(U\right)$ 的平面微分方程 (17.1) 是结构稳定的. 那么:

a) 方程 (17.1) 仅含有限个平衡点和周期轨.

b) 方程 (17.1) 中任意点 $x\in \overline{U}$ 的 $\omega$ 极限集 $\omega \left(x\right)$ 仅含有平衡点和周期点.

安德罗诺夫-蓬特里亚金 (Andronov-Pontryagin) 定理 $f\in X_{+}^1$ 的平面微分方程 (17.1) 是结构稳定的, 当且仅当

a) $\overline{U}$ 内所有平衡点和周期轨是双曲的.

b) 不存在分界线, 也就是说, 没有连接鞍点和鞍点的异宿轨和同宿轨.

17.1.4.2 结构稳定的时间离散系统

在时间离散动力系统 (17.3) 情形下,即 $\phi :M\to M$ ,令 $U\subset M\subset {\mathbb{R}}^n$ 是有界连通开集,并且其边界光滑. 令 ${\mathrm{Diff}}^1\left(U\right)$ 是 $M$ 上所有同胚映射构成的度量空间, 装配着 $U$ 上的 $C^1$ 度量. 假设集合 ${\mathrm{Diff}}_{+}^1\left(U\right)\subset \mathrm{Diff}\left(U\right)$ 包含满足 $\phi \left(\overline{U}\right)\subset U$ 的微分同胚 $\phi$ . 映射 $\phi \in {\mathrm{Diff}}_{+}^1\left(U\right)$ (和相应的动力系统 (17.3)) 称为结构稳定的,如果存在 $\delta >0$ 使得任意满足 $\rho \left(\phi ,\psi \right)<\delta$ 的 $\psi \in {\mathrm{Diff}}_{+}^1\left(U\right)$ 与 $\phi$ 是拓扑共轭的.

17.1.4.3 通有性质

1. 定义

度量空间 $\left(M,\rho \right)$ 上的关于元素的性质称为通有的,如果 $M$ 中满足该性质的元素全体构成的集合 $B$ 是第二贝尔 (Baire) 纲集,即 $B$ 可表示为 $B=\underset{m=1,2,\cdots }{\cap }{B}_m$ , 其中,每个集合 $B_m$ 是开集且在 $M$ 中稠密.

$◼\mathbf{A}$: 集合 $\mathbb{R}$ 和 $\mathbb{I}\subset \mathbb{R}$ (无理数) 是第二贝尔纲集, $\mathbb{Q}$ 不是第二贝尔纲集.

$◼\mathbf{B}$: 仅用稠密性刻画通有性是不充分的: $\mathbb{Q}\subset \mathbb{R}$ 和 $\mathbb{I}\subset \mathbb{R}$ 都是稠密的,但不都是通有的.

$◼\mathbf{C}$: $\mathbb{R}$ 中集合的勒贝格测度 $\lambda$ 和贝尔纲集之间没有关系. 集合 $B=\underset{k=1,2\cdots }{\cap }{B}_k$ , 其中 $B_k=\underset{n\ge 0}{\cup }\left(a_n-\frac{1}{k{2}^n},a_n+\frac{1}{k{2}^n}\right),\mathbb{Q}={\left\{a_n\right\}}_{n=0}^{\mathrm{\infty }}$ 表示有理数集合,是第二贝尔纲集. 另一方面,因为 $B_k\supset B_{k+1},\lambda \left(B_k\right)<+\mathrm{\infty }$ ,所以 $\lambda \left(B\right)=\underset{k\to \mathrm{\infty }}{lim}{B}_k\le$$\underset{k\to \mathrm{\infty }}{lim}\frac{2}{k}\frac{1}{1-1/2}=0.$

2. 平面系统的通有性质、哈密顿系统

对于平面微分方程, $X_{+}^1\left(U\right)$ 中的全体结构稳定系统构成的集合是开集且在 $X_{+}^1$ (U)中稠密. 因此,对于平面系统,结构稳定系统是通有的. 在 $X_{+}^1\left(U\right)$ 导出的平面系统中, 随着时间增加, 趋于有限个平衡点和周期轨中某一个的轨道也是通有的. 拟周期轨不是通有的. 在特定假设下, 对于哈密顿系统, 微分方程的拟周期轨在小扰动下可以保持. 因此, 哈密顿系统不是通有的.

在 ${\mathbb{R}}^4$ 中,给定作用变量一角变量下的哈密顿系统 ${\dot{j}}_1=0,{\dot{j}}_2=0,{\dot{\mathrm{\Theta }}}_1=\frac{\partial H_0}{\partial j_1},{\dot{\mathrm{\Theta }}}_2=$ $\frac{\partial H_0}{\partial j_2}$ ,其中,哈密顿函数 $H_0\left(j_1,j_2\right)$ 是解析函数. 显然,系统的解为 $j_1=c_1,j_2=$ $c_2,{\mathrm{\Theta }}_1={\omega }_{1}t+c_3,{\mathrm{\Theta }}_2={\omega }_{2}t+c_4$ ,其中, $c_1,\cdots ,c_4$ 是常数, ${\omega }_1,{\omega }_2$ 依赖与 $c_1,c_2$ . 关系 $\left(j_1,j_2\right)=\left(c_1,c_2\right)$ 确定了一个不变环面 $T^2$ . 现在考虑扰动的哈密顿函数 $H_0\left(j_1,j_2\right)+$ $\epsilon H_1\left(j_1,j_2,{\mathrm{\Theta }}_1,{\mathrm{\Theta }}_2\right)$ ,其中 $H_1$ 是解析函数, $\epsilon >0$ 是小参数.

根据柯尔莫哥洛夫-阿诺德-莫泽(Kolmogorov-Arnold-Moser) 定理(KAM定理), 若 $H_0$ 是非退化的,即 $det\left(\frac{{\partial }^2{H}_0}{\partial j_k^2}\right)\ne 0$ ,则在扰动的哈密顿系统中,当 $\epsilon >0$ 充分小时, 大多数的不变非共振环面不会消失, 但会有轻微的变形. “大多数环面” 指的是: 当 $\epsilon$ 趋于 0 时,这些环面余集的勒贝格测度趋于 0 . 用 ${\omega }_1$ 和 ${\omega }_2$ 描述的上述环面称为非共振的,如果存在常数 $c>0$ ,使得对任意正整数 $p$ 和 $q$ ,有不等式$\left|\frac{{\omega }_1}{{\omega }_2}-\frac{p}{q}\right|\ge \frac{c}{q^{2.5}}$

3. 非游荡点、莫尔斯-斯梅尔系统

设 ${\left\{{\phi }^t\right\}}_{t\in \mathbb{R}}$ 是 $n$ 维紧致的可定向流形 $M$ 上的动力系统. 点 $p\in M$ 称为 $\left\{{\phi }^t\right\}$ 的非游荡点,如果对于 $p$ 的任意邻域 $U_p\subset M$ ,有

$$\begin{array}{}\text{(17.27)}& \mathrm{\forall }T>0\mathrm{\exists }t,\left|t\right|\ge T:{\phi }^t\left(U_p\right)\cap U_p\ne \varnothing .\end{array}$$

稳态解和周期轨仅含有非游荡点.

方程 (17.1) 生成的动力系统中,所有非游荡点全体构成的集合 $\mathrm{\Omega }\left({\phi }^t\right)$ 是闭的, $\left\{{\phi }^t\right\}$ 的不变集,并且包括所有周期轨和所有 $M$ 中点的 $\omega$ 极限集.

$M$ 上光滑向量场生成的动力系统 ${\left\{{\phi }^t\right\}}_{t\in \mathbb{R}}$ 称为莫尔斯-斯梅尔 (Morse-Smale) 系统, 如果满足下面的条件:

(1)系统只有有限个平衡点和周期轨, 且它们都是双曲的.

(2) 所有平衡点和周期轨的稳定流形和不稳定流形是横截相交的.

(3) 全体非游荡点的集合仅包含平衡点和周期轨

帕利-斯梅尔 (Palis-Smale) 定理 莫尔斯-斯梅尔系统是结构稳定的.

帕利-斯梅尔定理的逆定理不成立: 当 $n=3$ 时,存在含有无穷多周期轨的结构稳定系统.

当 $n\ge 3$ 时,结构稳定系统不是通有的.