Appearance
18.2.9 割平面法
1. 问题的提法和求解原理
设考虑有界区域
这里
看作另一个约束,并且在约束
这个方法的基本想法是通过极小点
首先, 确定凸多面体
由线性规划问题
相对于
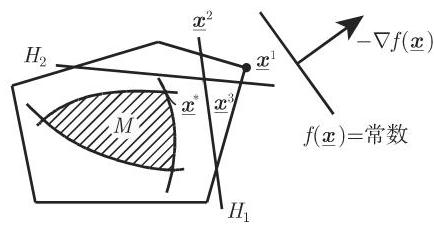
图 18.13 为割平面法的示意图.
2. 凯利 (Kelley) 方法
不同方法之间的区别在于分离平面的选取. 采用凯利方法,
函数
超平面
Appearance
设考虑有界区域
这里
看作另一个约束,并且在约束
这个方法的基本想法是通过极小点
首先, 确定凸多面体
由线性规划问题
相对于
图 18.13 为割平面法的示意图.

不同方法之间的区别在于分离平面的选取. 采用凯利方法,
函数
超平面