14.1.1 连续性、可微性

14.1.1.1 复函数的定义

与实函数类似,对于复值可以指定复值与其对应,即对于值 $z=x+\mathrm{i}y$ ,可以指定一个复数 $w=u+\mathrm{i}v$ 与其对应,其中 $u=u\left(x,y\right),v=v\left(x,y\right)$ 是两个实变量 $x,y$ 的实函数. 这个关系被记为 $w=f\left(z\right)$ . 函数 $w=f\left(z\right)$ 是从复数 $z$ 平面到复数 $w$ 平面的一个映射.

可以与实变量的实函数那样类似地定义复函数 $w=f\left(z\right)$ 的极限、连续性和导数的概念.

14.1.1.2 复函数的极限

一个函数 $f\left(z\right)$ (在 $z_0$ 处) 的极限 (limit) 等于复数 $w_0$ ,如果当 $z$ 趋于 $z_0$ 时函数值 $f\left(z\right)$ 趋于 $w_0$ :

$$\begin{array}{}\text{(14.1a)}& w_0=\underset{z\to z_0}{lim}f\left(z\right).\end{array}$$

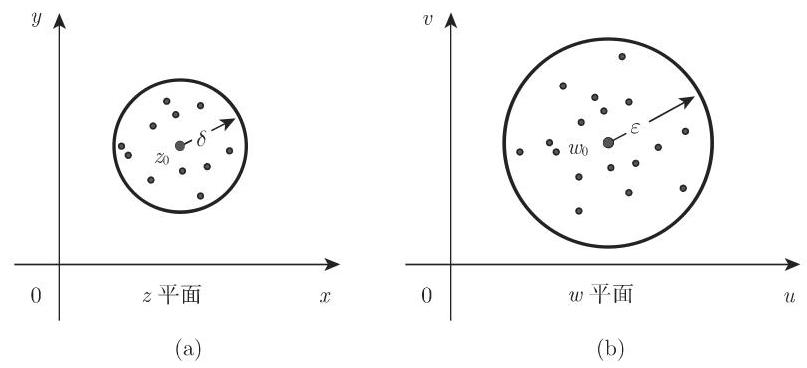
换言之: 对于任何正的 $\epsilon$ ,存在一个 (实的) $\delta >0$ ,使得对满足 (14.1b) 的每个 $z$ ,也许除了 $z_0$ 本身外,成立不等式 (14.1c):

$$\begin{array}{}\text{(14.1b)}& \left|z_0-z\right|<\delta \end{array}$$$$\begin{array}{}\text{(14.1c)}& \left|w_0-w\right|<\epsilon \end{array}$$

几何意义如下: 以 $z_0$ 为圆心, $\delta$ 为半径的圆中的任一点 $z$ ,也许除了 $z_0$ 本身外,被映为 $w$ 平面中以 $w_0$ 为圆心, $\epsilon$ 为半径的圆中的点 $w=f\left(z\right)$ ,如图 14.1 所展示. 半径为 $\delta$ 和 $\epsilon$ 的两个圆也被称为邻域 $U_{\delta }\left(z_0\right)$ 和 $U_{\epsilon }\left(w_0\right)$ .

14.1.1.3 连续的复函数

一个函数 $w=f\left(z\right)$ 在 $z_0$ 处是连续的,如果它在该处有极限,并且该极限与函数在该处的值相等,即,如果对 $w$ 平面中的点 $w_0=f\left(z_0\right)$ 的任意给定的小邻域 $U_{\epsilon }\left(w_0\right)$ ,在 $z$ 平面中存在 $z_0$ 的一个邻域 $U_{\delta }\left(z_0\right)$ ,使得对于每个点 $z\in U_{\delta }\left(z_0\right)$ ,有 $w=f\left(z\right)\in U_{\epsilon }\left(w_0\right)$ . 如图 14.1 所示,例如, $U_{\epsilon }\left(w_0\right)$ 是围绕点 $w_0$ 的半径为 $\epsilon$ 的圆. 用通常的记号, $f$ 的连续性表达为 ${}^1$

$$\begin{array}{}\text{(14.2)}& \underset{z\to z_0}{lim}f\left(z\right)=f\left(z_0\right)\text{ 或 }\underset{\delta \to 0}{lim}f\left(z_0+\delta \right)=f\left(z_0\right).\end{array}$$

14.1.1.4 复函数的可微性

函数 $w=f\left(z\right)$ 在 $z$ 处是可微的,如果微商

$$\begin{array}{}\text{(14.3)}& \frac{\mathrm{\Delta }w}{\mathrm{\Delta }z}=\frac{f\left(z+\mathrm{\Delta }z\right)-f\left(z\right)}{\mathrm{\Delta }z}\end{array}$$

当 $\mathrm{\Delta }z\to 0$ 时有不依赖于 $\mathrm{\Delta }z$ 趋于零的方式的极限. 这个极限用 $f^{\prime }\left(z\right)$ 表示,并被称为 $f\left(z\right)$ 的导数.

函数 $f\left(z\right)=\mathrm{Re}z=x$ 在任何点 $z=z_0$ 处都不是可微的,因为平行于 $x$ 轴趋于 $z_0$ 时该差商的极限为 1,而平行于 $y$ 轴趋于 $z_0$ 时该值为零.