Appearance
5.9.6 基于知识的模糊系统
在技术和非技术领域中, 单位区间上的多值模糊逻辑有多种应用的可能性. 一般性概念包括: 量和特征数的模糊化, 通过适当的知识基础和运算将它们聚合, 以及如有必要还包括将可能的模糊结果集合逆模糊化.
5.9.6.1 Mamdani 方法
下列步骤用于模糊控制过程:
(1)法则基础 设,例如,对于第
其中
(2) 模糊化算法一般地,误差
(3) 聚合模 具有各自不同权的起作用的法则将与一个代数运算相结合并应用于逆模糊化.
(4)决策模 在逆模糊化过程中将对控制量给出清晰值. 应用逆模糊化运算, 非模糊值的量是从可能值即清晰量的集合中确定的. 这个量表示应该怎样确定系统的控制参数以保持偏差极小.
模糊控制意味着步骤 (1)---(4) 是重复的, 直到达到取得最小的偏差及其变化的目的.
5.9.6.2 菅野方法
菅野 (Sugeno) 方法也用来设计模糊控制程序. 它与 Mamdani 概念的差别在于法则基础和逆模糊化方法. 它有下列步骤:
(1)法则基础 法则基础由下列形式的法则组成:
其中各个记号的意义是:
(2) 模糊算法 对于每个法则
(3) 决策模 非模糊值的量是从
中的
在此不进行 Mamdani 方法的逆模糊化. 问题是要得到有效的权参数
5.9.6.3 认知系统
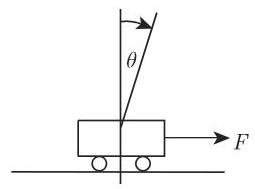
为了清楚地了解方法, 我们应用 Mamdani 方法研究下面著名的例子: 摆的校准 (使它垂直于它的活动底座)(图 5.78). 控制过程的目的是保持摆的平衡使得摆杆是垂直的, 即对于垂直方向的角位移及角速度为零. 这必须通过一个作用于摆的下端的力
对于每个被测量的值
活动底座上的逆摆(图 5.78)
(1) 建模 对于集合
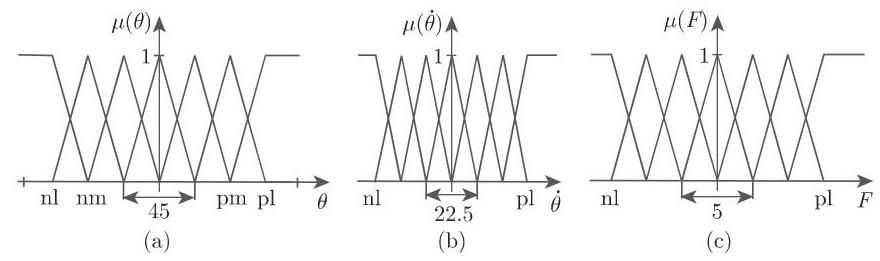
为了数学建模, 如同我们对于模糊推理所指出的 (参见第 572 页 5.9.4), 必须对这些语言项中的每一个设定一个模糊集 (图 5.77).
(2) 选取值的范围
角的值:
. 角速度的值:
. 力的值:
.
输入量
(3) 法则的选取 考虑下面的表,其中有
表: 含 19 个有实际意义的法则的法则基础
nl | nm | ns | ps | pm | pl | ||
nl | ps | pl | |||||
nm | pm | ||||||
ns | ns | ps | |||||
nl | nm | ns | ps | pm | pl | ||
ps | ns | ps | pm | ||||
pm | nm | ||||||
pl | nl | ns |
得到输出集
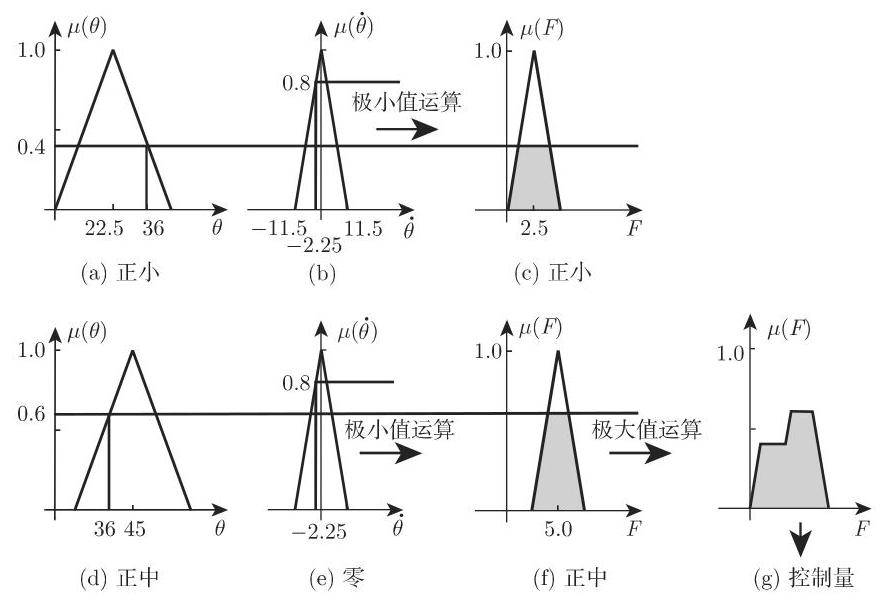
(4) 决策逻辑 法则
a) 这样得到的模糊集的计算要通过算子聚合 (参见第 570 页极大-极小复合
(5.394)
c) 其余 17 个法则得到对于前提的满足等级等于零, 即得到本身是零的模糊集.
(5) 逆模糊化意味着要应用逆模糊化方法确定控制量.
应用重心法和极大值准则法得到控制量的值
(6) 注记
(1)“基于知识”的路线建立在法则基础之上, 因而最终目的以法则偏差最小为中心.
(2) 应用逆模糊化时迭代过程被引进, 它最终抵达分区空间的中心, 即得到零控制量.
(3) 每个非线性特征域可以通过选择紧域上的适当参数以任意精确度逼近.
5.9.6.4 基于知识的插值系统
1. 插值技巧
可以借助模糊逻辑建立插值技巧. 模糊系统是处理模糊信息的系统. 有可能将它们用于函数逼近或插值. 一个可用来研究这个性质的简单的模糊系统是 Sugeno 控制器. 它有
的法则
结论的简单选取能够省去昂贵的逆模糊化,并且输出值
2. 限于 1 维情形
对于仅有一个输入
(1) 对于每个法则
(2) 至多有两个法则在两个相继的结点间满足. 如果
(3) 因为隶属函数是正的,所以输出
对于常数结论,项
对于输入
一般地,若选取