Appearance
15.2.1 拉普拉斯变换的性质
15.2.1.1 拉普拉斯变换、原始空间和像空间
1. 拉普拉斯变换的定义
设
存在,则定义了复变量
在一些文献中, 拉普拉斯变换经常也以瓦格纳或拉普拉斯-卡森变换的形式
出现.
2. 收敛性
拉普拉斯积分
(1)
该性质是
(2) 若原函数
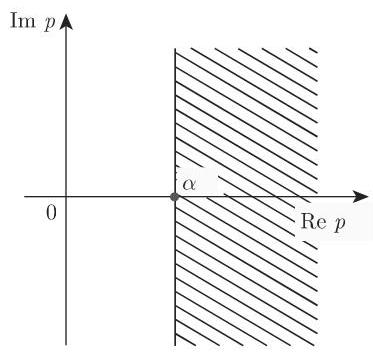
(3)拉普拉斯变换的逆变换.
利用公式
可由像函数得到原函数.
该复积分的积分路径是平行于虚轴的直线
15.2.1.2 拉普拉斯变换的运算规则
运算规则是从原始域内运算到变换空间内运算的映射.
此后, 原函数将用小写字母表示, 变换用相应的大写字母表示.
1. 加法或线性法则
只要变换存在, 函数线性组合的拉普拉斯变换是拉普拉斯变换式相同的线性组合,即对于常数
(15.9)
2. 相似法则
拉普拉斯变换:
类似地, 对于逆变换, 有
图 15.3 展示了相似法则在正弦函数中的一个应用.
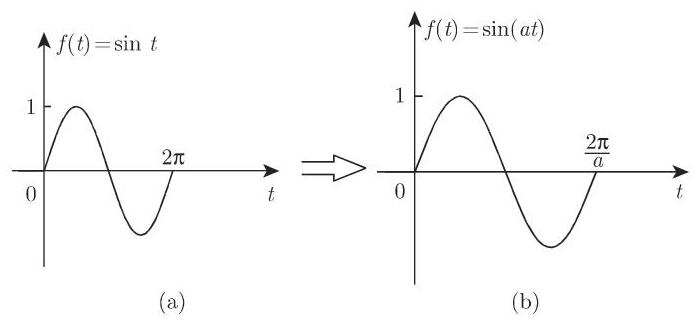
运用相似法则, 可给出
3. 平移法则
(1)向右平移 原函数向右平移
(2)向左平移 原函数向左平移
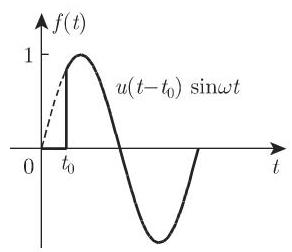
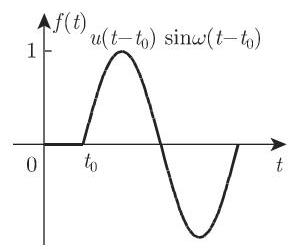
图 15.4 和图 15.5 显示了余弦函数的向右平移和直线的向左平移.
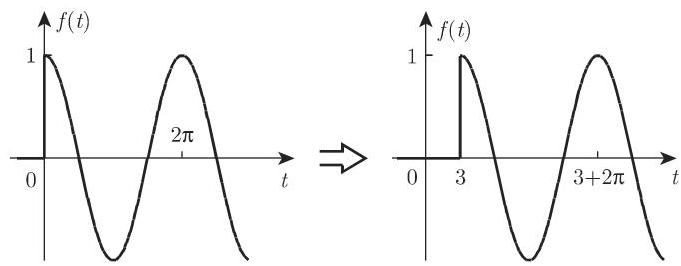
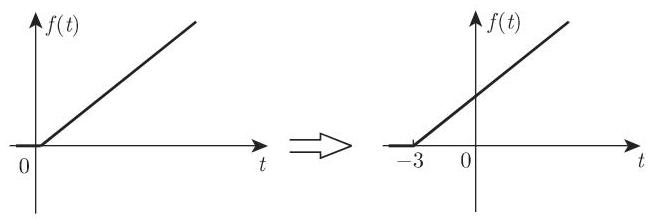
4. 频移定理
原函数乘以
5. 在原始空间内的微分
当
方程 (15.13) 给出了下述拉普拉斯积分表达式, 可用于逼近拉普拉斯积分:
(15.14)
6. 在像空间内的微分
变换的
7. 在原始空间内的积分
原函数积分的变换等于原函数的变换乘以
在单积分的特殊情况下, 有
成立. 在原始空间内, 若初始值为 0 , 则微分和积分互逆.
8. 在像空间内的积分
(15.18)
仅当
9. 除法法则
在 (15.18) 中,对于
成立. 若积分 (15.19) 式存在,极限
10. 对参数的微分和积分
借助这些公式, 有时可根据已知积分计算拉普拉斯积分.
11. 卷积
(1) 在原始空间内的卷积 两个函数
方程 (15.21) 也称为区间(0, t)上的单侧卷积. 傅里叶变换产生双侧卷积(区间
① 此处
图 15.6 显示了两函数的卷积. 我们可运用卷积定理确定原函数:
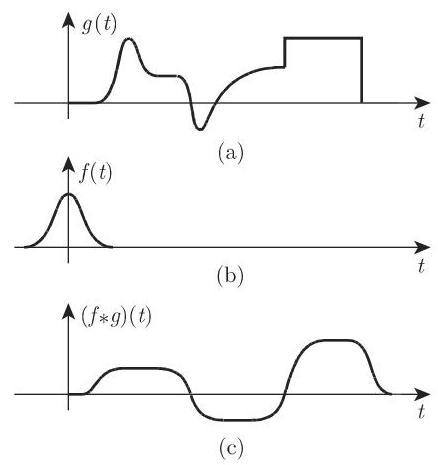
a) 分解像函数
b) 确定变换
c) 在原始空间中,结合
(2)在像空间内的卷积 (复卷积)
积分路径为沿着与虚轴平行的直线. 在第一个积分中,必须选定
15.2.1.3 特殊函数的变换
1. 阶梯函数
在
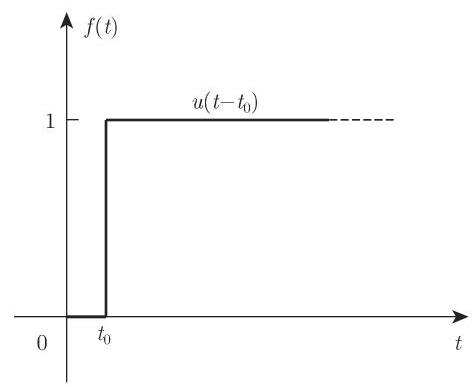
. (图 15.9)
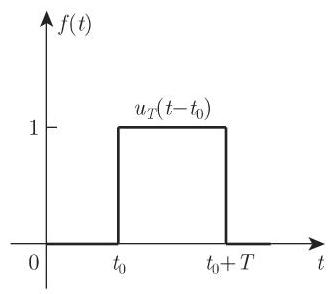
2. 矩形脉冲
高度为 1、宽度为
3. 脉冲函数 (狄拉克
(也可参见第 912 页 12.9.5.4) 脉冲函数
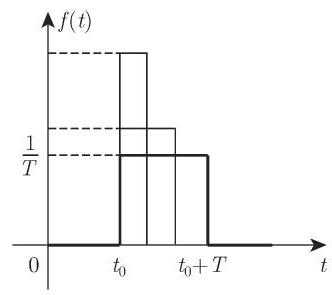
对于连续函数
比如
等关系式, 通常在广义函数论中进行研究 (参见第 912 页 12.9.5.3).
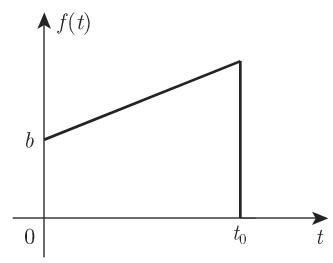
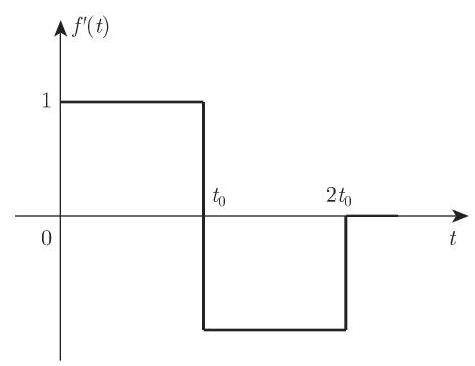
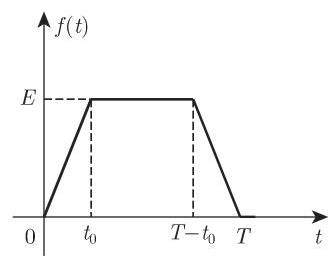
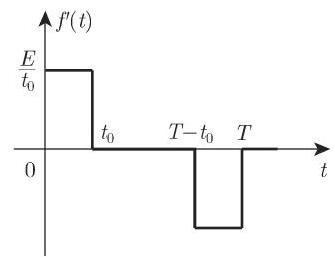
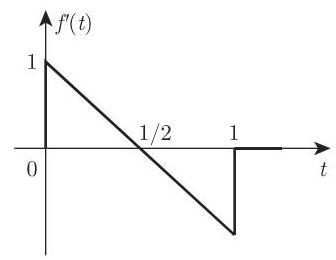
4. 分段可微函数
分段可微函数的变换可借助
其中,
若跳跃首先出现在导数中, 则有类似的公式成立. 在这种方式下, 我们可以轻松确定由任意高度抛物线组成的曲线所对应函数的变换, 例如, 实证研究曲线. 当正式应用 (15.13) 时,在跳跃情况下,数值
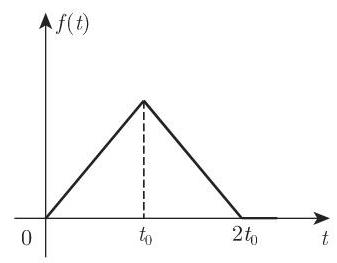
5. 周期函数
周期为
得到.
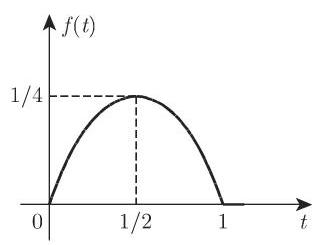
15.2.1.4 狄拉克
在利用线性微分方程描述某些技术系统时,函数
通过引入所谓的广义函数(分布),提供了一种解决方法,从而可以使
1.
类似于 (15.28) 式,脉冲函数
更深入的
这些函数具有共同的性质:
(1)
(2)
(3)
2.
(1)
(2)
(3)
此处考虑了
(4)
重复进行