4.1.4 矩阵的算术运算

1. 矩阵的相等

两个矩阵 $\mathbf{A}=\left(a_{\mu \nu }\right)$ 和 $\mathbf{B}=\left(b_{\mu \nu }\right)$ 相等,如果它们有相同的大小,并且对应元素相等:

$$\begin{array}{}\text{(4.20)}& \mathbf{A}=\mathbf{B}\text{,当 }{a}_{\mu \nu }=b_{\mu \nu }\left(\mu =1,\cdots ,m;\nu =1,\cdots ,n\right).\end{array}$$

2. 加法和减法

两个矩阵仅当大小相同时才可能相加减. 两个矩阵的和 (差) 由它们的对应元素相加 (相减) 得到:

$$\begin{array}{}\text{(4.21a)}& \mathbf{A}\pm \mathbf{B}=\left(a_{\mu \nu }\right)\pm \left(b_{\mu \nu }\right)=\left(a_{\mu \nu }\pm b_{\mu \nu }\right).\end{array}$$

$◼$ $\left(\begin{array}{ccc}1& 3& 7\\ 2& -1& 4\end{array}\right)+\left(\begin{array}{ccc}3& -5& 0\\ 2& 1& 4\end{array}\right)=\left(\begin{array}{ccc}4& -2& 7\\ 4& 0& 8\end{array}\right)$ .

对于矩阵的加法, 交换律和结合律成立:

a) 交换律 $\mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}$ ;(4.21b)

b) 结合律 $\left(\mathbf{A}+\mathbf{B}\right)+\mathbf{C}=\mathbf{A}+\left(\mathbf{B}+\mathbf{C}\right)$ .(4.21c)

3. 数乘矩阵

实数或复数 $\alpha$ 与大小为(m, n)的矩阵 $\mathbf{A}$ 相乘,就是用 $\alpha$ 乘 $\mathbf{A}$ 的每个元素:

$$\begin{array}{}\text{(4.22a)}& \alpha \mathbf{A}=\alpha \left(a_{\mu \nu }\right)=\left(\alpha a_{\mu \nu }\right).\end{array}$$

$◼3\left(\begin{array}{ccc}1& 3& 7\\ 0& -1& 4\end{array}\right)=\left(\begin{array}{ccc}3& 9& 21\\ 0& -3& 12\end{array}\right).$

由 (4.22a) 可知, 我们显然可以提出矩阵每个元素都含有的常数因子. 对于矩阵与标量的乘法, 乘法交换律、结合律及分配律都成立:、及

a) 交换律 $\alpha A=A\alpha$ ;(4.22b)

b) 结合律 $\alpha \left(\beta \mathbf{A}\right)=\left(\alpha \beta \right)\mathbf{A}$ ;(4.22c)

c) 分配律 $\left(\alpha \pm \beta \right)\mathbf{A}=\alpha \mathbf{A}\pm \beta \mathbf{A};\alpha \left(\mathbf{A}\pm \mathbf{B}\right)=\alpha \mathbf{A}\pm \alpha \mathbf{B}$ .(4.22d)

4. 数除以矩阵

用标量 $\gamma \ne 0$ 除矩阵即用 $\alpha =1/\gamma$ 乘矩阵.

5. 两矩阵相乘

(1)矩阵乘积 两个矩阵 $\mathbf{A}$ 和 $\mathbf{B}$ 的乘积 $\mathbf{AB}$ 仅当左边因子 $\mathbf{A}$ 的行数等于右边因子 $\mathbf{B}$ 的列数时才可计算. 如果 $\mathbf{A}$ 是大小为(m, n)的矩阵,那么矩阵 $\mathbf{B}$ 的大小必须是(n, p),并且乘积 $\mathbf{AB}$ 是大小为(m, p)的矩阵 $\mathbf{C}=\left(c_{\mu \nu }\right)$ . 元素 $c_{\mu \nu }$ 等于左边因子 $\mathbf{A}$ 的第 $\mu$ 行与右边因子 $\mathbf{B}$ 的第 $\mu$ 列的标量积:

$$\begin{array}{}\text{(4.23)}& \mathbf{AB}=\left(\sum _{\nu =1}^n{a}_{\mu \nu }{b}_{\nu \lambda }\right)=\left(c_{\mu \lambda }\right)=\mathbf{C}\left(\mu =1,2,\cdots ,m;\lambda =1,2,\cdots ,p\right).\end{array}$$

$\mathbf{A}=\left(\begin{array}{ccc}1& 3& 7\\ 2& -1& 4\\ -1& 0& 1\end{array}\right),\mathbf{B}=\left(\begin{array}{cc}3& 2\\ -5& 1\\ 0& 3\end{array}\right)$ ,依照公式 (4.23),积矩阵 $\mathbf{C}$ 的元素 $c_{22}=2\cdot 2-1\cdot 1+4\cdot 3=15$ .

(2) 矩阵乘积的不相等 即使乘积 $AB$ 和 $BA$ 都存在,通常 $AB\ne BA$ ,也就是说,乘法交换律一般不成立. 如果等式 $\mathbf{AB}=\mathbf{BA}$ 成立,那么我们称矩阵 $\mathbf{A}$ 和 $\mathbf{B}$ 是可换的或互相交换的.

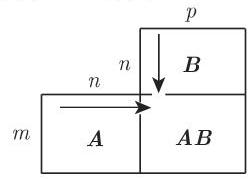
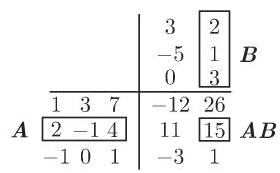
(3) 法尔克 (Falk) 格式 矩阵乘法 $AB=C$ 可以借助法尔克格式实现 (图 4.1). 积矩阵 $\mathbf{C}$ 的元素 $c_{\mu \nu }$ 恰好出现在 $\mathbf{A}$ 的第 $\mu$ 行与 $\mathbf{B}$ 的第 $\lambda$ 列的交点.

应用法尔克格式,矩阵 ${\mathbf{A}}_{(3,3)}$ 与 ${\mathbf{B}}_{(3,2)}$ 相乘如图 4.2 所示.

(4) 复元素矩阵 ${\mathbf{K}}_1$ 和 ${\mathbf{K}}_2$ 的乘法 对于两个复元素矩阵的乘法,可以应用依据公式 (4.2b) 得到的实部和虚部分解式: ${\mathbf{K}}_1={\mathbf{A}}_1+\mathrm{i}{\mathbf{B}}_1,{\mathbf{K}}_2={\mathbf{A}}_2+\mathrm{i}{\mathbf{B}}_2$ ,这里 ${\mathbf{A}}_1,{\mathbf{B}}_1,{\mathbf{A}}_2,{\mathbf{B}}_2$ 是实矩阵. 作此分解后,相乘得到一些矩阵之和,其中各加项是实矩阵之积.

$\mathbf{I}\left(\mathbf{A}+\mathrm{i}\mathbf{B}\right)\left(\mathbf{A}-\mathrm{i}\mathbf{B}\right)={\mathbf{A}}^2+{\mathbf{B}}^2+\mathrm{i}\left(\mathbf{B}\mathbf{A}-\mathbf{A}\mathbf{B}\right)$ (关于矩阵的幂,参见第 370 页 4.1.5,8.). 当然,在做这些矩阵的乘法时,应当考虑到交换律对于乘法一般不成立, 即矩阵 $\mathbf{A}$ 与 $\mathbf{B}$ 通常是不可互相交换的.

6. 两个向量的标量积和并积

如果将向量 $\underset{―}{a}$ 和 $\underset{―}{b}$ 分别看作 1 行矩阵和 1 列矩阵,那么依据矩阵乘法法则,存在两种可能将它们相乘.

如果 $\underset{―}{\mathbf{a}}$ 的大小是 $\left(1,n\right),\underset{―}{\mathbf{b}}$ 的大小是(n,1),那么它们的乘积的大小是(1,1),即是一个数. 它称作两个向量的标量积. 反之,如果 $\underset{―}{a}$ 有大小 $\left(n,1\right),\underset{―}{b}$ 有大小(1, m), 那么它们的乘积的大小是(n, m),即是一个矩阵. 这个矩阵称为这两个向量的并积.

(1) 两个向量的标量积 行向量 ${\underset{―}{\mathbf{a}}}^{\mathrm{T}}=\left(a_1,a_2,\cdots ,a_n\right)$ 与列向量 $\underset{―}{\mathbf{b}}=(b_1$ , ${b_2,\cdots ,b_n)}^{\mathrm{T}}$ (两者都有 $n$ 个元素) 的标量积定义为数,

$$\begin{array}{}\text{(4.24)}& {\underset{―}{\mathbf{a}}}^{\mathrm{T}}\underset{―}{\mathbf{b}}={\underset{―}{\mathbf{b}}}^{\mathrm{T}}\underset{―}{\mathbf{a}}=a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n=\sum _{\mu =1}^n{a}_{\mu }{b}_{\mu }.\end{array}$$

乘法交换律对于标量积一般不成立,因此必须准确保持 ${\underset{―}{a}}^{\mathrm{T}}$ 和 $\underset{―}{b}$ 的顺序. 如果交换乘法顺序,那么乘积 $\underset{―}{\mathbf{b}}{\underset{―}{\mathbf{a}}}^{\mathrm{T}}$ 将是并积.

(2) 两个向量的并积或张量积 $n$ 维行向量 $\underset{―}{\mathbf{a}}={(a_1,a_2,\cdots ,a_n)}^{\mathrm{T}}$ 与 $m$ 维列向量 ${\underset{―}{b}}^{\mathrm{T}}=\left(b_1,b_2,\cdots ,b_m\right)$ 的并积定义为下列大小为(n, m)的矩阵:

$$\begin{array}{}\text{(4.25)}& \underset{―}{\mathbf{a}}{\underset{―}{\mathbf{b}}}^{\mathrm{T}}=\left(\begin{array}{cccc}{a}_1{b}_1& a_1{b}_2& \cdots & a_1{b}_m\\ a_2{b}_1& a_2{b}_2& \cdots & a_2{b}_m\\ ⋮& ⋮& & ⋮\\ a_n{b}_1& a_n{b}_2& \cdots & a_n{b}_m\end{array}\right).\end{array}$$

在此乘法交换律一般也不成立.

(3) 关于两个向量的向量积概念的提示 在多向量或交错张量的范围中有所谓外积, 其三维形式就是熟知的向量积或叉积 (参见第 247 页 3.5.1.5, 2. 及其后). 本书不讨论高秩多向量的外积.

7. 矩阵的秩

(1)定义 矩阵 $\mathbf{A}$ 中线性无关的列向量的最大个数 $r$ 等于线性无关的行向量的最大个数. 这个数 $r$ 称为矩阵的秩,并且记作 $\mathrm{rank}\left(\mathbf{A}\right)=r$ .

(2)关于矩阵的秩的一些说明

a) 因为在 $m$ 维向量空间中不存在多于 $m$ 个线性无关的行向量或列向量 (参见第 490 页 5.3.8.2),所以大小为(m, n)的矩阵 $\mathbf{A}$ 的秩不可能大于 $m$ 和 $n$ 中的较小者:

$$\begin{array}{}\text{(4.26a)}& \mathrm{rank}\left({\mathbf{A}}_{(m,n)}\right)=r\le min\{m,n\}.\end{array}$$

b) 方阵 ${\mathbf{A}}_{(n,n)}$ 称为正则矩阵,如果

$$\begin{array}{}\text{(4.26b)}& \mathrm{rank}\left({\mathbf{A}}_{(n,n)}\right)=r=n.\end{array}$$

大小为(n, n)的方阵是正则的,当且仅当它的行列式不为零,即 $det\mathbf{A}\ne 0$ (参见第 373 页 $4.2.2,3.)$ . 不然它是奇异方阵.

c) 因此,对于奇异方阵 ${\mathbf{A}}_{(n,n)}$ ,即 $det\mathbf{A}=0$ ,有

$$\begin{array}{}\text{(4.26c)}& \mathrm{rank}\left({\mathbf{A}}_{(n,n)}\right)=r<n.\end{array}$$

d) 零矩阵0的秩等于零:

$$\begin{array}{}\text{(4.26d)}& \mathrm{rank}\left(\mathbf{0}\right)=0\text{.}\end{array}$$

e) 矩阵的和及积的秩满足关系式

$$\begin{array}{}\text{(4.26e)}& \left|\mathrm{rank}\left(\mathbf{A}\right)-\mathrm{rank}\left(\mathbf{B}\right)\right|\le \mathrm{rank}\left(\mathbf{A}+\mathbf{B}\right)\le \mathrm{rank}\left(\mathbf{A}\right)+\mathrm{rank}\left(\mathbf{B}\right),\end{array}$$$$\begin{array}{}\text{(4.26f)}& \mathrm{rank}\left(\mathbf{A}\mathbf{B}\right)\le min\{\mathrm{rank}\left(\mathbf{A}\right),\mathrm{rank}\left(\mathbf{B}\right)\}.\end{array}$$

(3) 确定秩的法则 初等变换不改变矩阵的秩. 其中初等变换是

a) 交换两列或两行.

b) 用数乘一行或一列.

c) 将一行加到另一行或将一列加到另一列.

为了确定它们的秩, 可以通过适当的行的线性组合将每个矩阵变换为这种形式: 在第 $\mu$ 行中至少最初 $\mu -1$ 个元素等于零 $\left(\mu =2,3,\cdots ,m\right)$ (高斯算法原理,参见第 417 页 4.5.2.4). 在变换得到的矩阵中非零向量的行向量的个数等于矩阵的秩 $r$ .

8. 逆矩阵

对于正则矩阵 $\mathbf{A}=\left(a_{\mu \nu }\right)$ 总存在 (对于乘法的) 逆矩阵 ${\mathbf{A}}^{-1}$ ,即

$$\begin{array}{}\text{(4.27a)}& \mathbf{A}{\mathbf{A}}^{-1}={\mathbf{A}}^{-1}\mathbf{A}=\mathbf{I}.\end{array}$$

${\mathbf{A}}^{-1}=\left({\beta }_{\mu \nu }\right)$ 的元素是

$$\begin{array}{}\text{(4.27b)}& {\beta }_{\mu \nu }=\frac{{\mathbf{A}}_{\nu \mu }}{det\mathbf{A}}\end{array}$$

其中 ${\mathbf{A}}_{\nu \mu }$ 是属于矩阵 $\mathbf{A}$ 的元素 $a_{\nu \mu }$ 的余因子 (参见第 372 页 4.2.1,1.). 为实际计算 ${\mathbf{A}}^{-1}$ ,可应用第 373 页 4.2.2,2. 所给出的方法. 在大小为(2,2)的矩阵的情形中, 有

$$\begin{array}{}\text{(4.28)}& \mathbf{A}=\left(\begin{array}{ll}a& b\\ c& d\end{array}\right),{\mathbf{A}}^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right).\end{array}$$

注 为什么不定义矩阵的除法, 而是应用逆矩阵进行计算? 这与除法不能唯一地定义的事实相关. 方程

$$\mathbf{B}{\mathbf{X}}_1=\mathbf{A}\text{ 与 }{\mathbf{X}}_2\mathbf{B}=\mathbf{A}\text{ (其中 }\mathbf{B}\text{ 正则) }$$

的解

$$\begin{array}{}\text{(4.29)}& {\mathbf{X}}_1={\mathbf{B}}^{-1}\mathbf{A}\text{ 与 }{\mathbf{X}}_2=\mathbf{A}{\mathbf{B}}^{-1}\end{array}$$

一般是不同的.

9. 正交矩阵

如果对于方阵 $\mathbf{A}$ 关系式

$$\begin{array}{}\text{(4.30)}& {\mathbf{A}}^{\mathrm{T}}={\mathbf{A}}^{-1}\text{ 或 }\mathbf{A}{\mathbf{A}}^{\mathrm{T}}={\mathbf{A}}^{\mathrm{T}}\mathbf{A}=\mathbf{I}\end{array}$$

成立, 则称它是一个正交矩阵, 这就是说, 它的任一行与另一行的转置的标量积, 或任一列的转置与另一列的标量积都为零, 同时任一行与它自己的转置或任一列的转置与它自己的标量积都等于 1 .

正交矩阵有下列性质:

a) 正交矩阵的转置和逆也是正交矩阵; 并且其行列式

$$\begin{array}{}\text{(4.31)}& \text{det}\mathbf{A}=\pm 1\text{.}\end{array}$$

b) 正交矩阵的积也是正交矩阵.

旋转矩阵 $\mathbf{D}$ 也是正交矩阵,它被用来刻画坐标系的旋转,其元素是新轴向的方向余弦 (参见第 284 页 3.5.3.3, 2.).

10. 酉矩阵

如果对于复元素矩阵 $\mathbf{A}$ 关系式

$$\begin{array}{}\text{(4.32)}& {\left({\mathbf{A}}^{\ast }\right)}^{\mathrm{T}}={\mathbf{A}}^{-1}\text{ 或 }\mathbf{A}{\left({\mathbf{A}}^{\ast }\right)}^{\mathrm{T}}={\left({\mathbf{A}}^{\ast }\right)}^{\mathrm{T}}\mathbf{A}=\mathbf{I}\end{array}$$

成立, 则称它是一个酉矩阵. 在实数情形, 酉矩阵与正交矩阵相同.