Appearance
5.2.4 等价性和序关系
对于集合
1. 等价关系
若与集合
等价关系的例
2. 等价类、分拆
(1) 等价类 集合
称为
这些等价类形成一个新的集合,即商集
幂集
(2) 分解定理 集合
集合
3. 次序关系
集合
次序关系的例
注 如果
4. 哈塞图
有限有序集可以通过哈塞图表示: 设在有限集
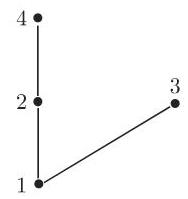
哈塞图是一个 “简化” 的箭头图, 其中所有的圈、箭头以及由关系的传递性产生的箭都被省略. 图 5.7 给出集合
Appearance
对于集合
若与集合
(1) 等价类 集合
称为
这些等价类形成一个新的集合,即商集
幂集
(2) 分解定理 集合
集合
集合
注 如果
有限有序集可以通过哈塞图表示: 设在有限集
哈塞图是一个 “简化” 的箭头图, 其中所有的圈、箭头以及由关系的传递性产生的箭都被省略. 图 5.7 给出集合
