13.1.2 标量场

13.1.2.1 标量场或标量点函数

如果对于空间一个子集的每个点 $P$ 都指定一个数 (标量值) $U$ ,则记为

$$\begin{array}{}\text{(13.6a)}& U=U\left(P\right),\end{array}$$

并称 (13.6a) 为一个标量场 (scalar field) (或标量函数 (scalar function)). -个物体的温度、密度、位势等都是标量场的例子.

一个标量场 $U=U\left(P\right)$ 可以被视作

$$\begin{array}{}\text{(13.6b)}& U=U\left(\overrightarrow{r}\right),\end{array}$$

其中 $\overrightarrow{r}$ 是具有一个给定极 0 (参见第 243 页 3.5.1.1,6.) 的点 $P$ 的位置向量.

13.1.2.2 标量场的一些重要特殊情形

1. 平面场

如果所论函数只是对于空间中一个平面的点有定义, 则它就是一个平面场.

2. 中心场

如果一个函数在离一个称为中心的固定点 $C\left({\overrightarrow{r}}_1\right)$ 有相同距离的所有点 $P$ 处有相同的值, 那么它被称为是一个中心对称场 (central symmetrc field), 或中心场 (central field),或球面场 (spherical field). 该函数 $U$ 仅依赖于距离 $\overline{CP}=\left|\overrightarrow{r}\right|$ :

$$\begin{array}{}\text{(13.7a)}& U=f\left(\left|\overrightarrow{r}\right|\right).\end{array}$$

• 一个点状源的强度场, 例如, 在极点处一个点光源的亮度场, 可以用离光源的距离 $\left|\overrightarrow{r}\right|=r$ 被描述为

$$\begin{array}{}\text{(13.7b)}& U=\frac{c}{r^2}\left(c\text{ 为常数 }\right).\end{array}$$

3. 轴向场

如果函数 $U$ 在位于离一条直线 (场的轴) 有相同距离的所有点 $P$ 处有相同的值, 那么该场被称为是一个柱面对称场 (cylindrically symmetric field), 或轴对称场 (axially symmetric field), 或简单地称为轴向场 (axiial field).

13.1.2.3 标量场的坐标表示

如果空间的一个子集的点用它们的坐标, 例如笛卡儿坐标、柱面坐标, 或球面坐标给出, 则一般地, 相应的标量场 (13.6a) 由一个 3 个变量的函数所表示:

$$\begin{array}{}\text{(13.8a)}& U=\mathrm{\Phi }\left(x,y,z\right),U=\mathrm{\Psi }\left(\rho ,\phi ,z\right)\text{ 或 }U=\chi \left(r,\vartheta ,\phi \right).\end{array}$$

在平面场的情形, 两个变量的函数就足够了. 它有笛卡儿坐标和极坐标的形式:

$$\begin{array}{}\text{(13.8b)}& U=\mathrm{\Phi }\left(x,y\right)\text{ 或 }U=\mathrm{\Psi }\left(\rho ,\phi \right).\end{array}$$

一般地, (13.8a) 和 (13.8b) 中的函数被假设是连续的, 也许除了在间断性的某些点、 曲线或曲面上. 这些函数有形式:

对于中心场

$$\begin{array}{}\text{(13.9a)}& U=U\left(\sqrt{x^2+y^2+z^2}\right)=U\left(\sqrt{{\rho }^2+z^2}\right)=U\left(r\right),\end{array}$$

其中坐标系的原点是场的极点 (pole),

对于轴向场

$$\begin{array}{}\text{(13.9b)}& U=U\left(\sqrt{x^2+y^2}\right)=U\left(\rho \right)=U\left(r\sin \vartheta \right),\end{array}$$

其中 $z$ 轴是场的轴.

用球面坐标处理中心场最方便, 用柱面坐标处理轴向场最方便.

13.1.2.4 一个场的等值面和等值线

1. 等值面

一个等值面是空间中所有点 $P$ 的集合,在这些点处函数 (13.6a) 有常数值

$$\begin{array}{}\text{(13.10a)}& U=U\left(P\right)=\text{ 常数. }\end{array}$$

不同的常数 $U_0,U_1,U_2,\cdots$ 定义不同的等值面. 对于每个点,都存在一个等值面通过该点, 除非在该点处函数没有定义. 在目前所用的 3 个坐标系中的等值面方程是

$$U=\mathrm{\Phi }\left(x,y,z\right)=\text{ 常数,}U=\mathrm{\Psi }\left(\rho ,\phi ,z\right)=\text{ 常数,}U=\chi \left(r,\vartheta ,\phi \right)=\text{ 常数. }$$

(13.10b)

不同场的等值面的例子:

$◼\mathbf{A}$: $U=\overrightarrow{c}\overrightarrow{r}=c_{x}x+c_{y}y+c_{z}z$ : 平行平面.

$◼\mathbf{B}$: $U=x^2+2y^2+4z^2$ : 在相同位置的相似椭球面.

$◼\mathbf{C}$: 中心场: 同心球面.

$◼\mathbf{D}$: 轴向场: 同轴柱面.

2. 等值线

在平面场中等值线替代了等值面. 它们满足方程

$$\begin{array}{}\text{(13.11)}& U=\text{ 常数. }\end{array}$$

通常,对于 $U$ 的相等的间隔来画等值线,它们中的每一条都被标以相应的 $U$ 值 (参见第 915 页图 13.3).

$◼$ 熟知的例子有天气图上的等压线和地形图上的等高线.

在一些特别的情形, 等值面退化为一些点或线, 等值线退化为一些分离的点.

下列一些场的等值线被展示在图 13.4 中: (a) $U=xy$ ,(b) $U=\frac{y}{x^2}$ ,(c) $U=$$x^2+y^2={\rho }^2,\left(\mathrm{d}\right)U=\frac{1}{\rho }.$

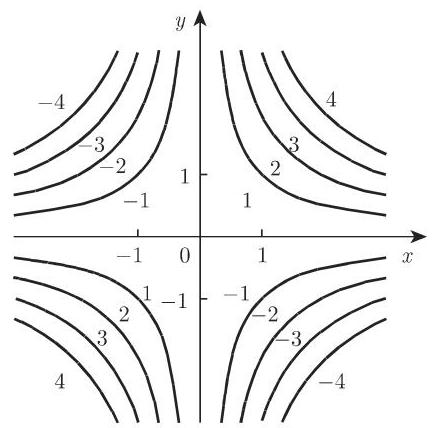
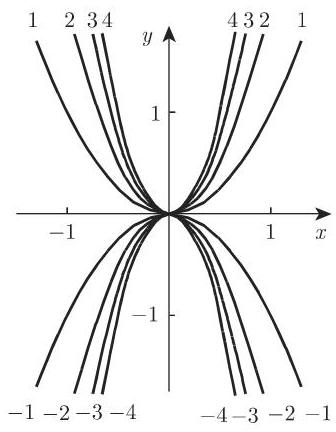
(a) (b)