1.5.2 几何表示

1.5.2.1 向量表示

与实数在数轴上的表示类似,复数可表示为所谓高斯平面上的点: 数 $z=a+\mathrm{i}b$ 用横坐标为 $a$ 、纵坐标为 $b$ 的点表示 (图 1.5). 实数在横轴上,横轴也称为实轴,纯虚数在纵轴上, 纵轴也称为虚轴. 在高斯平面上, 每个点由其位置向量或径向量唯一给出 (参见第 243 页 3.5.1.1, 6.), 故任一复数都对应一个向量, 该向量的起点为原点, 且指向复数所定义的点. 因此, 复数可表示为点或向量 (图 1.6).

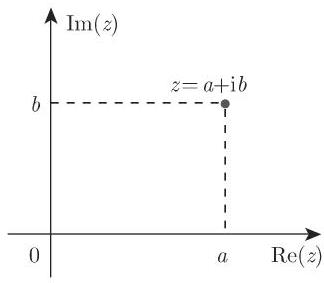
1.5.2.2 复数的相等

两个复数相等是指其实部和虚部对应相等. 从几何观点来看, 两个复数相等是指其对应的位置向量相等. 反之, 则称两个复数不相等. 对复数而言, 概念 “大于” 和 “小于” 是无意义的.

1.5.2.3 复数的三角形式

形式

$$\begin{array}{}\text{(1.132a)}& z=a+\mathrm{i}b\end{array}$$

称为复数的代数形式. 使用极坐标可得复数的三角形式(图 1.7):

$$\begin{array}{}\text{(1.132b)}& z=\rho \left(\cos \phi +\mathrm{i}\sin \phi \right).\end{array}$$

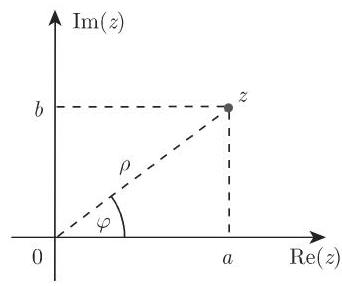
一个点的位置向量的长度 $\rho =\left|z\right|$ 称为复数的绝对值或复数的模,角 $\phi$ 称为复数的辐角,用弧度度量,记为 $\arg z$ :

$$\rho =\left|z\right|,\phi =\arg z=\omega +2k\pi ,$$

其中, $0\le \rho <\mathrm{\infty },-\pi <\omega \le +\pi ,k=0,\pm 1,\pm 2,\cdots$ .(1.132c)

$\phi$ 称为复数的辐角主值.

对于一个点来说, $\rho ,\phi$ 和 $a,b$ 的关系,与该点笛卡儿坐标和极坐标的关系是相同的 (参见第257页 $3.5.2.2,3.)$ :

$$\begin{array}{}\text{(1.133a)}& a=\rho \cos \phi ,\end{array}$$$$\begin{array}{}\text{(1.133b)}& b=\rho \sin \phi \end{array}$$$$\begin{array}{}\text{(1.133c)}& \rho =\sqrt{a^2+b^2}\end{array}$$$$\begin{array}{}\text{(1.133d)}& \phi =\{\begin{array}{ll}\arccos \frac{a}{\rho },& b\ge 0,\rho >0,\\ -\arccos \frac{a}{\rho },& b<0,\rho >0,\\ \text{ 无定义,}& \rho =0,\end{array}\end{array}$$$$\begin{array}{}\text{(1.133e)}& \phi =\{\begin{array}{ll}\arctan \frac{b}{a},& a>0,\\ \frac{\pi }{2},& a=0,b>0,\\ -\frac{\pi }{2},& a=0,b<0,\\ \arctan \frac{b}{a}+\pi ,& a<0,b\ge 0,\\ \arctan \frac{b}{a}-\pi ,& a<0,b<0.\end{array}\end{array}$$

复数 $z=0$ 的绝对值等于 0,其辐角 $\arg 0$ 无定义.

1.5.2.4 复数的指数形式

表达式

$$\begin{array}{}\text{(1.134a)}& z=\rho {\mathrm{e}}^{\mathrm{i}\phi }\end{array}$$

称为复数的指数形式,其中 $\rho$ 是复数的模, $\phi$ 是辐角.

欧拉关系式是公式

$$\begin{array}{}\text{(1.134b)}& {\mathrm{e}}^{\mathrm{i}\phi }=\cos \phi +\mathrm{i}\sin \phi \end{array}$$

• 复数表达式有三种形式:

**a) $z\ast \ast =1+\mathrm{i}\sqrt{3}$ (代数形式).

**b) $z\ast \ast =2\left(\cos \frac{\pi }{3}+\mathrm{i}\sin \frac{\pi }{3}\right)$ (三角形式).

**c) $z\ast \ast =2{\mathrm{e}}^{\mathrm{i}\frac{\pi }{3}}$ (指数形式),对应复数的辐角主值.

该式成立并不仅限于主值.

$$z=1+\mathrm{i}\sqrt{3}=2\exp \left[\mathrm{i}\left(\frac{\pi }{3}+2k\pi \right)\right]$$$$=2\left[\cos \left(\frac{\pi }{3}+2k\pi \right)+\mathrm{i}\sin \left(\frac{\pi }{3}+2k\pi \right)\right]\left(k=0,\pm 1,\pm 2,\cdots \right).$$

1.5.2.5 共轭复数

两个复数 $z$ 和 $z^{\ast }$ 称为共轭复数,若其实部相等,虚部互为相反数:

$$\begin{array}{}\text{(1.135a)}& \mathrm{Re}\left(z^{\ast }\right)=\mathrm{Re}\left(z\right),\mathrm{Im}\left(z^{\ast }\right)=-\mathrm{Im}\left(z\right).\end{array}$$

共轭复数对应点的几何解释是关于实轴的点对称. 共轭复数有相同的绝对值, 其辐角仅相差一个符号:

$$\begin{array}{}\text{(1.135b)}& z=a+\mathrm{i}b=\rho \left(\cos \phi +\mathrm{i}\sin \phi \right)=\rho {\mathrm{e}}^{\mathrm{i}\phi },\end{array}$$$$\begin{array}{}\text{(1.135c)}& z^{\ast }=a-\mathrm{i}b=\rho \left(\cos \phi -\mathrm{i}\sin \phi \right)=\rho {\mathrm{e}}^{-\mathrm{i}\phi }.\end{array}$$

通常使用记号 $\overline{z}$ 代替 $z^{\ast }$ ,表示 $z$ 的共轭复数.