Appearance
19.5.3 有限元方法 (FEM)
在现代计算机出现后, 有限元方法成为求解偏微分方程的最重要的技术. 也容易说明这种强有力的方法产生的结果.
对于不同类型的应用, 有限元方法有很不相同的实施方式, 故这里仅介绍其基本思想. 它类似于数值求解常微分方程边值问题的里茨法 (参见第 1266 页 19.4.2.2), 也涉及样条插值 (参见第 1293 页 19.7).
有限元方法有如下步骤.
1. 定义变分问题
由已知边值问题形成变分问题. 以如下边值问题为例说明其过程:
在
在微分方程 (19.144) 两边乘以在
应用高斯求积公式 (参见第 945 页 13.2.2.1,(2)),将
其中
2. 三角形剖分
将积分区域
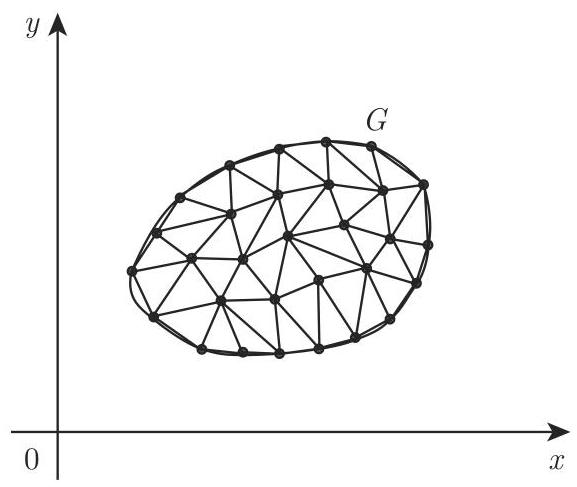
注 为避免数值上的困难, 三角形剖分中应该不包含钝角三角形.
单位正方形的三角形剖分见图 19.8. 从坐标为
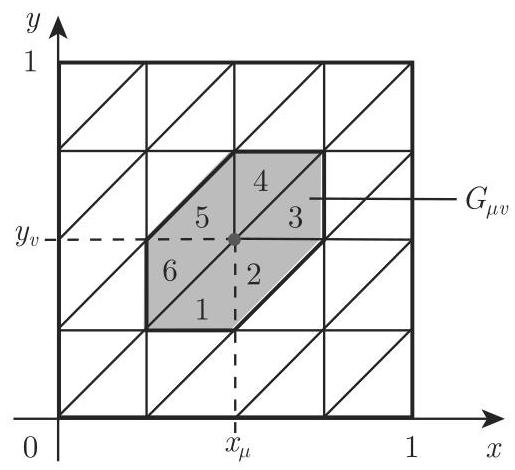
3. 求解
对所求的函数
已经足够. 假设近似函数在相邻三角形间必须连续, 故最终的解也是连续的.
(19.147) 中的系数
确定适当的系数
(1)
(2)
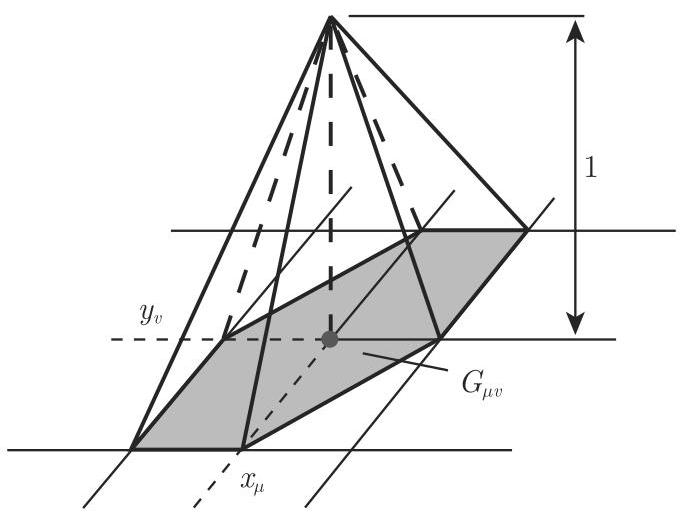
满足
由 (19.151) 得
类似有
4. 计算解的系数
解的系数
其中
(19.155)
在计算
因总是在面积为
类似得到关于变量
计算 (19.154) 的右端项
其中
于是变分方程 (19.154) 导致确定解系数的线性方程组
表 19.1 有限元法附表
面域 | 图示 | 三角形 | |||
(1) |  | 0 | 0 | ||
22 | |||||
33 | |||||
0 | 0 | ||||
55 | |||||
6 | |||||
0 | |||||
(2) | 0 | ||||
 | 0 | ||||
(3) | |||||
 | |||||
0 | |||||
(4) | 0 | ||||
 | 0 | ||||
(5) | 0 | 0 | |||
 | 0 | ||||
(6) | |||||
 | |||||
0 | |||||
0 | |||||
(7) |  | 0 |
(19.158)
注 (1) 若解的系数可由 (19.158) 确定,则由 (19.148) 得到的
(2)若积分区域必须被不规则的三角形网格覆盖, 则要引入三角形坐标 (也称重心坐标). 这样容易确定点关于三角形网格的位置, 又因为每个三角形容易变换为以
(3) 若需要改善解的精度或可微性, 则必须应用分片二次或三次函数以得到假设的近似 (见 [19.28]).
(4) 在实际应用中, 通常得到高维的线性方程组. 这正是发展许多特殊方法的原因, 例如, 方程组的结构依赖于三角形网格的自动剖分和单元的实际列举. 关于有限元方法的详细介绍见 [19.21], [19.13], [19.28].