14.3.1 复项级数的收敛性

14.3.1.1 复数序列的收敛性

复数的一个无穷序列 $z_1,z_2,\cdots ,z_n,\cdots$ 有一个极限 $z\left(z=\underset{n\to \mathrm{\infty }}{lim}{z}_n\right)$ ,如果对每个任意给定的正数 $\epsilon$ ,存在一个 $n_0$ ,使得对每个 $n>n_0$ 成立不等式 $\left|z-z_n\right|<\epsilon$ , 即,从某个 $n_0$ 开始,诸数 $z_n,z_{n+1},\cdots$ 所表示的点都在以 $z$ 为圆心,半径为 $\epsilon$ 的圆内.

$◼$ 如果表达式 $\{\sqrt[n]{a}\}$ 表示具有最小非负辐角的根,那么对于任意复数 $a\ne 0$ 极限等式 $\underset{n\to \mathrm{\infty }}{lim}\{\sqrt[n]{a}\}=1$ 成立 (图 14.39).

14.3.1.2 复项无穷级数的收敛性

具有复项 $a_i$ 的一个级数 $a_1+a_2+\cdots +a_n+\cdots$ 收敛到数 $s$ ,称为该级数的和,如果部分和 $s_n$

$$\begin{array}{}\text{(14.44)}& s_n=a_1+a_2+\cdots +a_n\left(n=1,2,\cdots \right)\end{array}$$

的序列收敛到 $s$ . 在 $z$ 平面上用折线连接相应于诸数 $s_n=a_1+a_2+\cdots +a_n$ 的点, 那么收敛性就意味着折线的末端趋近于点 $s$ .

$$\text{- A:}\mathrm{i}+\frac{{\mathrm{i}}^2}{2}+\frac{{\mathrm{i}}^3}{3}+\frac{{\mathrm{i}}^4}{4}+\cdots \text{. - B:}\mathrm{i}+\frac{{\mathrm{i}}^2}{2}+\frac{{\mathrm{i}}^3}{2^2}+\cdots \text{(图 14.40).}$$

一个级数被称为绝对收敛的 (absolutely convergent) (见 $◼$ B),如果绝对值级数 $\left|a_1\right|+\left|a_2\right|+\left|a_3\right|+\cdots$ 也是收敛的. 级数被称为条件收敛的 (conditionally convergent) (见 $◼\mathrm{A}$ ),如果该级数收敛,但不是绝对收敛的. 如果级数的诸项是函数 $f_i\left(z\right)$ ,如

$$\begin{array}{}\text{(14.45)}& f_1\left(z\right)+f_2\left(z\right)+\cdots +f_n\left(z\right)+\cdots ,\end{array}$$

那么其和是一个函数,它对于使得函数值级数收敛的那些 $z$ 值有定义.

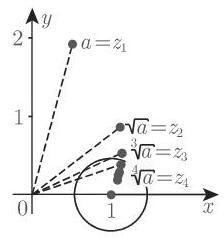
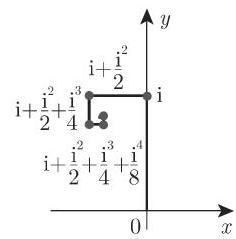
14.3.1.3 复项幂级数

1. 收敛性

一个具有复系数的幂级数有形式

$$\begin{array}{}\text{(14.46a)}& P\left(z-z_0\right)=a_0+a_1\left(z-z_0\right)+a_2{(z-z_0)}^2+\cdots +a_n{(z-z_0)}^n+\cdots ,\end{array}$$

其中 $z_0$ 是复平面中的一个固定点,诸系数是复常数 (也可以有实值). 对于 $z_0=0$ , 幂级数有形式

$$\begin{array}{}\text{(14.46b)}& P\left(z\right)=a_0+a_{1}z+a_2{z}^2+\cdots +a_n{z}^n+\cdots .\end{array}$$

如果对于某个值 $z_1$ 幂级数 $P\left(z-z_0\right)$ 收敛,那么在以 $z_0$ 为心,半径为 $r=\left|z_1-z_0\right|$ 的圆内部的每个点 $z,P\left(z-z_0\right)$ 是绝对且一致收敛的.

2. 收敛圆

一个复幂级数的收敛性区域与发散性区域之间的界限是一个唯一确定的圆周. 如在实数情形一样, 如果极限

$$\begin{array}{}\text{(14.47)}& r=\frac{1}{\underset{n\to \mathrm{\infty }}{lim}\sqrt[n]{\left|a_n\right|}}\text{ 或 }r=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{a_n}{a_{n+1}}\right|\end{array}$$

存在,则就确定了该圆的半径. 如果级数除了在 $z=z_0$ 外处处发散,则 $r=0$ ; 如果它处处收敛,则 $r=\mathrm{\infty }$ . 幂级数在收敛性区域的边界圆周上的性状必须逐点地加以考察.

收敛半径为 1 的幂级数 $P\left(z\right)=\sum _{n=1}^{\mathrm{\infty }}\frac{z^n}{n}$ 当 $z=1$ 时是发散的 (调和级数),当 $z=-1$ 时是收敛的 (根据交错级数的莱布尼茨准则 (参见第 621 页 7.2.3.3,1.)). 除了点 $z=1$ 之外,这个幂级数对于单位圆周 $\left|z\right|=1$ 上所有别的点都是收敛的.

3. 收敛圆中幂级数的导数

在收敛圆内部, 每个幂级数表示一个解析函数. 通过逐项求导得到其导数. 导数级数与原级数有相同的收敛半径.

4. 收敛圆中幂级数的积分

通过对 $f\left(z\right)$ 的幂级数的逐项积分可以得到积分 ${\int }_{z_0}^{z}f\left(\zeta \right)\mathrm{d}\zeta$ 的幂级数表达式. 收敛半径保持不变.