12.8.6 正非线性算子

为了成功地应用绍德尔不动点定理, 要求适当选择一个集合, 使得所考虑的算子将之映入其自身. 在应用中, 尤其是在非线性边值问题理论中, 常常考虑有序赋范函数空间和保持相应锥不变的正算子,或者保序增算子,即若 $x\le y\Rightarrow T\left(x\right)\le$ $T\left(y\right)$ . 如果不至于混淆 (例如,参见第 904 页 12.8.7),这些算子也可以称作单调算子.

设 $X=\left(X,X_{+},\parallel \cdot \parallel \right)$ 是一个有序巴拿赫空间, $X_{+}$ 是一闭锥,而 $\left[a,b\right]$ 是 $X$ 的一序区间. 如果 $X_{+}$ 是规范锥,并且 $T$ 是全连续 (不一定单调) 算子,满足 $T\left(\left[a,b\right]\right)\subset \left[a,b\right]$ . 那么 $T$ 在 $\left[a,b\right]$ 中至少有一个不动点 (图 12.6(b)).

注意,如果 $T$ 是定义在 $X$ 的 (o) 区间 (序区间) $\left[a,b\right]$ 上的单调增算子,并且将两个端点 $a,b$ 映入 $\left[a,b\right]$ ,即满足条件 $T\left(a\right)\ge a,T\left(b\right)\le b$ ,那么条件 $T\left(\left[a,b\right]\right)\subset \left[a,b\right]$ 自动成立. 于是两个序列

$$\begin{array}{}\text{(12.205)}& x_0=a,x_{n+1}=T\left(x_n\right)\left(n\ge 0\right)\text{ 和 }{y}_0=b,y_{n+1}=T\left(y_n\right)\left(n\ge 0\right)\end{array}$$

是适定的,即 $x_n,y_n\in \left[a,b\right],n\ge 0$ . 它们分别是单调增序列和单调减序列,即 $a=x_0\le x_1\le \cdots \le x_n\le \cdots$ 和 $b=y_0\ge y_1\ge \cdots \ge y_n\ge \cdots .T$ 的不动点 $x_{\ast },x^{\ast }$ 分别叫作最小不动点和最大不动点,是指对于 $T$ 的任意不动点 $z$ ,分别有不等式 $x_{\ast }\le z$ 和 $z\le x^{\ast }$ .

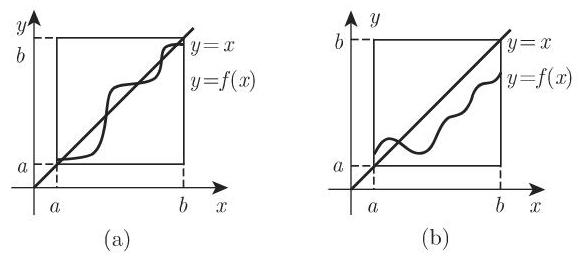
现在有如下命题 (图 12.6(a)): 设 $X$ 是有序巴拿赫空间, $X_{+}$ 是闭锥, $D\subset X$ , $T:D\to X$ 是连续单调算子. 设 $\left[a,b\right]\subset D$ 使得 $T\left(a\right)\ge a$ 和 $T\left(b\right)\le b$ . 那么 $T\left(\left[a,b\right]\right)\subset \left[a,b\right]$ ,并且如果下列条件之一满足,则算子 $T$ 在 $\left[a,b\right]$ 中有不动点:

**a) $X_{\ast \ast +}$ 是规范锥,且 $T$ 是紧算子;

**b) $X_{\ast \ast +}$ 是正则锥.

于是 (12.205) 中定义的序列 ${\left\{x_n\right\}}_{n=0}^{\mathrm{\infty }}$ 和 ${\left\{y_n\right\}}_{n=0}^{\mathrm{\infty }}$ 分别收敛于 $T$ 在 $\left[a,b\right]$ 中最小和最大不动点.

上解和下解的概念就是基于以上结论 (参见 [12.7], [12.13], [12.14]).