2.4.5 第 III 类三次曲线

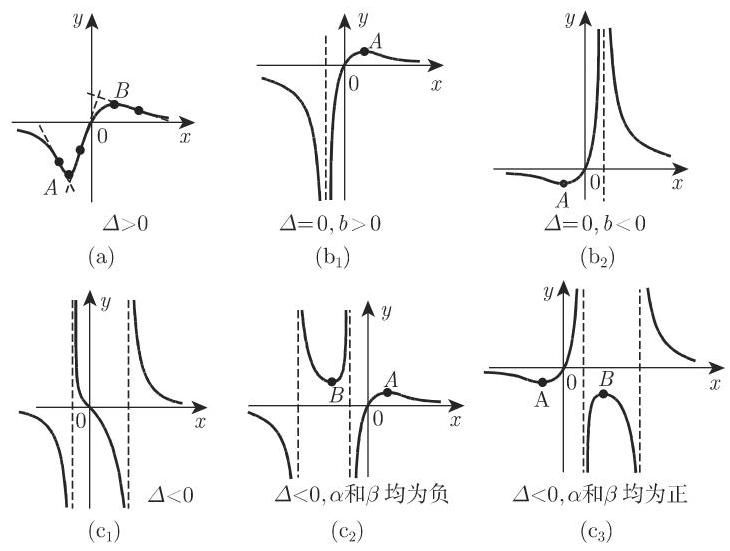
函数

$$\begin{array}{}\text{(2.49)}& y=\frac{x}{a{x}^2+bx+c}\left(a\ne 0,b\ne 0,c\ne 0\right)\end{array}$$

的图像为一过原点的三次曲线(第III类), $x$ 轴为它的一条渐近线 (图 2.20). 该函数的性状除了与 $a$ 和 $\mathrm{\Delta }=4ac-b^2$ 的符号有关外,当 $\mathrm{\Delta }<0$ ,还与方程 $a{x}^2+bx+c=0$ 的根 $\alpha ,\beta$ 的符号有关; 当 $\mathrm{\Delta }=0$ 时,与 $b$ 的符号有关. 在 $a>0$ 和 $a<0$ 两种情况中,仅考虑第一种情况,因为只需将 $y=\frac{x}{\left(-a\right)x^2-bx-c}$ 沿 $x$ 轴反射就可以得到第二种情况.

情形 $\mathrm{a})\mathrm{\Delta }>0$ 函数处处连续,它的值先由 0 减小到极小值,再增加到极大值, 最后再次减小到 0 .

曲线的极值点 $A,B$ 为 $\left(\pm \sqrt{\frac{c}{a}},\frac{-b\pm 2\sqrt{ac}}{\mathrm{\Delta }}\right)$ ,且曲线有三个拐点 (图 2.20(a)).

情形 $\mathrm{b})\mathrm{\Delta }=0$ 函数的性质与 $b$ 的符号有关,因此分为两种情况. 在每种情况中,函数都有一个间断点 $x=-\frac{b}{2a}$ 和一个拐点.

• $b>0$ : 函数值先由 0 减小到 $-\mathrm{\infty }$ ,经过一个间断点后,函数值又由 $-\mathrm{\infty }$ 增加到极大值,接着再减小到 $0\left(\text{图}2.20\left({\mathrm{b}}_1\right)\right)$ . 曲线的极值点为 $A\left(+\sqrt{\frac{c}{a}},\frac{1}{2\sqrt{ac}+b}\right)$ . - $b<0$ : 函数值先由 0 减小到极小值,再经过原点增加到 $+\mathrm{\infty }$ ,接着函数经过一个间断点后又由 $+\mathrm{\infty }$ 减小到 $0\left(\text{图}2.20\left({\mathrm{b}}_2\right)\right)$ . 曲线的极值点为 $A\left(-\sqrt{\frac{c}{a}},-\frac{1}{2\sqrt{ac}-b}\right)$ .

情形 $\mathbf{c})\mathbf{\Delta }<\mathbf{0}$ 函数有两个间断点 $x=\alpha ,x=\beta$ ; 其性质与 $\alpha ,\beta$ 的符号有关. - $\alpha ,\beta$ 的符号互异: 函数值先从 0 减小到 $-\mathrm{\infty }$ ,接着跳跃到 $+\mathrm{\infty }$ ,然后由 $+\mathrm{\infty }$ 减小到 $-\mathrm{\infty }$ ,且通过原点,随后又跳跃到 $+\mathrm{\infty }$ 并减小到 0 (图 2.20(c)). 函数无极值. - $\alpha ,\beta$ 均为负数: 函数值先从 0 减小到 $-\mathrm{\infty }$ ,接着跳跃到 $+\mathrm{\infty }$ ,然后减少到极小值后再次增加到 $+\mathrm{\infty }$ ,随后跳跃到 $-\mathrm{\infty }$ 并增加到极大值,最后逐渐减小至趋于 0 (图 $2.20\left({\mathrm{c}}_2\right)$ ).

极值点 $A,B$ 可以利用与 2.4 .5 中的情形 a) 类似的公式来计算.

• $\alpha ,\beta$ 均为正数: 函数值先从 0 减小到极小值,再增加到 $+\mathrm{\infty }$ ,接着跳跃到 $-\mathrm{\infty }$ ,增加到极大值并再次减小到 $-\mathrm{\infty }$ ,随后跳跃到 $+\mathrm{\infty }$ 且逐渐减小至趋于 0 (图 2.20(c)).

极值点 $A,B$ 可以利用与 2.4.5 情形 a) 类似的公式来计算.

在这三种情况中, 曲线都有一个拐点.