16.3.3 重要检验

数理统计学的一个根本问题就是从样本中推断关于总体的结论. 有两类最重要的问题如下.

(1) 分布类型已知,欲估计其参数. 分布的特征通常可由参数 $\mu$ 和 ${\sigma }^2$ 较好地表示 (此处, $\mu$ 是期望的精确值, ${\sigma }^2$ 是方差的精确值),因此,一个至关重要的问题是, 如何根据样本较好地估计参数?

(2) 关于参数的假设已知, 欲检验其是否正确. 最常出现的问题是:

a) 期望值是否等于一个已知数?

b) 两个总体的期望是否相等?

c) 能否用参数为 $\mu$ 和 ${\sigma }^2$ 的随机变量的分布拟合一个已知分布等？

正态分布在观察和测量中极其重要, 下面讨论对正态分布的拟合优度检验. 其基本思想也适用于其他分布.

16.3.3.1 对正态分布的拟合优度检验

在数理统计学中有不同的检验方法, 用于判断样本数据是否来自于正态分布. 此处讨论基于正态概率纸的图形检验和基于 ${\chi }^2$ 分布的数值检验 (“ ${\chi }^2$ 检验”).

1. 使用概率纸进行拟合优度检验

a) 概率纸的原理 在直角坐标系中, $x$ 轴采用等距刻度, $y$ 轴的刻度由下述方式得到: 对 $z$ 等距分割,但刻度为

$$\begin{array}{}\text{(16.130)}& y=\mathrm{\Phi }\left(z\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\mathrm{\infty }}^z{\mathrm{e}}^{-\frac{t^2}{2}}\mathrm{d}t.\end{array}$$

若随机变量 $X$ 服从期望为 $\mu$ 和方差为 ${\sigma }^2$ 的正态分布,则对于其分布函数 (参见第 1070 页 16.2.4.2), 有

$$\begin{array}{}\text{(16.131a)}& F\left(x\right)=\mathrm{\Phi }\left(\frac{x-\mu }{\sigma }\right)=\mathrm{\Phi }\left(z\right),\end{array}$$

即

$$\begin{array}{}\text{(16.131b)}& z=\frac{x-\mu }{\sigma }\end{array}$$

成立,故 $x$ 和 $z$ 之间有线性关系,满足(16.131c)

$$\begin{array}{cc}z& x\\ 0& \mu \\ 1& \mu +\sigma \\ -1& \mu -\sigma \end{array}$$

b) 概率纸的应用 对于样本数据, 把根据 (16.125) 计算的累计相对频率作为点的纵坐标, 组上界作为横坐标, 并把对应点描绘到概率纸上. 若这些点大致落在一条直线上 (偏差很小), 则随机变量可视为正态随机变量 (图 16.14).

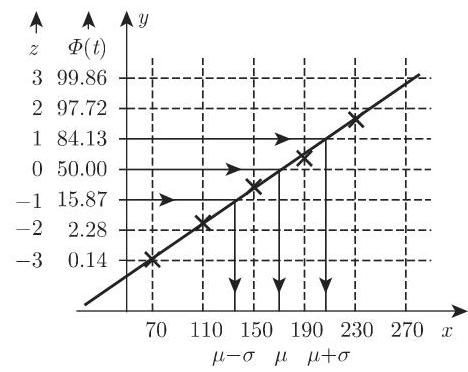
正如从图 16.14 中所看到的, 表 16.3 中的数据对应正态分布. 进一步可得到 $\mu \approx 176,\sigma \approx 37.5$ (由 $Z$ 轴上 0 和 $\pm 1$ 对应的 $x$ 值得到).

注 如果关于 $y$ 轴的刻度是等距的,则累计相对频率值 $F_i$ 更容易描绘到概率纸上, 这也意味着对于纵坐标的非等距刻度.

2. ${\chi }^2$ 拟合优度检验

欲检验随机变量 $X$ 是否服从正态分布 (参见第 1070 页 16.2.4.2),可把 $X$ 的范围分成 $k$ 组,第 $j$ 组 $\left(j=1,2,\cdots ,k\right)$ 的上限用 ${\xi }_j$ 表示. 令 $p_j$ 是 $X$ 落在第 $j$ 组的 “理论” 概率, 即

$$\begin{array}{}\text{(16.132a)}& p_j=F\left({\xi }_j\right)-F\left({\xi }_{j-1}\right),\end{array}$$

其中, $F\left(x\right)$ 是 $X$ 的分布函数 $\left(j=1,2,\cdots ,k;{\xi }_0\text{是第一组的下限,且}F\left({\xi }_0\right)=0\right)$ . 由于假定 $X$ 是正态变量,则

$$\begin{array}{}\text{(16.132b)}& F\left({\xi }_j\right)=\mathrm{\Phi }\left(\frac{{\xi }_j-\mu }{\sigma }\right)\end{array}$$

一定成立,其中 $\mathrm{\Phi }\left(x\right)$ 是标准正态分布的分布函数 (参见第 1070 页 16.2.4.2). 总体的参数 $\mu$ 和 ${\sigma }^2$ 通常是未知的,故用 $\overline{x}$ 和 $s^2$ 作为其近似值. 对 $X$ 的范围进行分解,使每一组的期望频数大于 5,即若样本容量为 $n$ ,则 $n{p}_j\ge 5$ . 对于容量为 $n$ 的样本 $\left(x_1,x_2,\cdots ,x_n\right)$ ,计算其相应的频数 $h_j$ (根据上述给定的分组),则随机变量

$$\begin{array}{}\text{(16.132c)}& {\chi }_S^2=\sum _{j=1}^k\frac{{(h_j-n{p}_j)}^2}{n{p}_j}\end{array}$$

近似服从 ${\chi }^2$ 分布. 若 $\mu$ 和 ${\sigma }^2$ 已知,则 ${\chi }^2$ 分布的自由度 $m=k-1$ ; 若 $\mu$ 和 ${\sigma }^2$ 其中之一需要根据样本进行估计,则 $m=k-2$ ; 若二者都需要根据 $\overline{x}$ 和 $s^2$ 估计, 则 $m=k-3$ .

如果随机变量 $X$ 服从正态分布 (近似 ${\chi }^2$ 检验),对于给定的统计量显著性水平 $\alpha$ 和自由度 $m$ ,检验在于对样本的试验量 ${\chi }_S^2$ 和 1460 页表 21.18 中相应的 ${\chi }_{\alpha ;m}^2$ 进行比较.

若确定了显著性水平 $\alpha$ ,并由 1460 页表 21.18 中得到了对应 ${\chi }^2$ 分布的分位数 ${\chi }_{\alpha ;k-i}^2$ ( $i$ 依赖于未知参数的个数),则 $P\left({\chi }_S^2\ge {\chi }_{\alpha ;k-i}^2\right)=\alpha$ 成立. 比较(16.132c) 式的 ${\chi }_S^2$ 值和上述分位数,若

$$\begin{array}{}\text{(16.132d)}& {\chi }_S^2<{\chi }_{\alpha ;k-i}^2\end{array}$$

成立,则接受样本来自于正态分布的假设. 该检验也称为 ${\chi }^2$ 拟合优度检验.

下述 ${\chi }^2$ 检验基于第 1087 页 16.3.2.1 的实例. 样本容量 $n=125$ ,且均值 $\overline{x}=176.32$ ,方差 $s^2=36.70$ ,它们可作为总体未知参数 $\mu$ 和 ${\sigma }^2$ 的近似值. 根据 (16.132a) 和 (16.132b) 进行计算后,再根据 (16.132c) 确定检验统计量 ${\chi }_S^2$ ,所得到的数据见表 16.4.

表 $16.4{\chi }^2$ 检验

${\xi }_j$	$h_j$	$\frac{{\xi }_j-\mu }{\sigma }$	$\mathrm{\Phi }\left(\frac{{\xi }_j-\mu }{\sigma }\right)$	$p_j$	$n{p}_j$	${(h_j-n{p}_j)}^2$ $n{p}_j$
70		-2.90	0.0019	0.0019	$\begin{array}{l}0.2375\\ 0.9375\\ 3.2125\\ 8.5857\end{array}\}12.9750$	0.00005
90		-2.35	0.0094	0.0075
110		-1.81	0.0351	0.0257
130		-1.26	0.1038	0.0687
150		-0.72	0.2358	0.1320	16.5000	0.1635
170	22	-0.17	0.4325	0.1967	24.5875	0.2723
190	30	0.37	0.6443	0.2118	26.4750	0.4693
210	27	0.92	0.8212	0.1769	22.1125	1.0803
230	9	1.46	0.9279	0.1067	13.3375	1.4106
250		2.01	0.9778	0.0499		0.0526
270	$\begin{array}{l}6\\ 3\end{array}\}9$	2.55	0.9946	0.0168	$\begin{array}{l}6.2375\\ 2.1000\end{array}\}8.3375$
						${\chi }_S^2=3.4486$

由最后一列可知 ${\chi }_S^2=3.4486$ . 因为要求 $n{p}_j\ge 5$ ,分组数量从 $k=11$ 减少到 $k^{\ast }=k-4=7$ . 为计算理论频率 $n{p}_j$ ,用样本估计值 $\overline{x}$ 和 $s^2$ 代替总体的 $\mu$ 和 ${\sigma }^2$ , 故相应 ${\chi }^2$ 分布的自由度个数减少 2,临界值为分位数 ${\chi }_{\alpha ;k^{\ast }-1-2}^2$ . 对于 $\alpha =0.05$ , 根据 1460 页表 21.18 可得到 ${\chi }_{0.05;4}^2=9.5$ ,因此,由不等式 ${\chi }_S^2<{\chi }_{0.05;4}^2$ 成立,假定样本来自于正态分布总体并无异议.

16.3.3.2 样本均值的分布

令 $X$ 是连续随机变量. 假设可从相应总体中取出任意多组容量为 $n$ 的样本, 则样本均值也是随机变量 $\overline{X}$ ,并且也是连续的.

1. 样本均值的置信概率

如果 $X$ 服从参数为 $\mu$ 和 ${\sigma }^2$ 的正态分布,则 $\overline{X}$ 也是参数为 $\mu$ 和 ${\sigma }^2/n$ 的正态随机变量,即 $\overline{X}$ 的密度函数 $\overline{f}\left(x\right)$ 比总体的密度函数 $f\left(x\right)$ 更集中于 $\mu$ 附近. 对任意 $\epsilon >0$ ,有

$$\begin{array}{}\text{(16.133)}& P\left(\left|X-\mu \right|\le \epsilon \right)=2\mathrm{\Phi }\left(\frac{\epsilon }{\sigma }\right)-1,P\left(\left|\overline{X}-\mu \right|\le \epsilon \right)=2\mathrm{\Phi }\left(\frac{\epsilon \sqrt{n}}{\sigma }\right)-1\end{array}$$

成立. 因此,当样本容量 $n$ 增加时,样本均值是 $\mu$ 的良好近似的概率也在增加.

$◼$ 当 $\epsilon =\frac{1}{2}\sigma$ 时,由 (16.133) 式得

$$P\left(\left|\overline{X}-\mu \right|\le \frac{1}{2}\sigma \right)=2\mathrm{\Phi }\left(\frac{1}{2}\sqrt{n}\right)-1,$$

表 16.5 列出了 $n$ 取不同值时所对应的概率值. 由表 16.5 可看出,比如,当样本容量 $n=49$ 时,样本均值 $\overline{x}$ 与 $\mu$ 之差小于 $\pm \frac{1}{2}\sigma$ 的概率是 $99.95\mathrm{\%}$ .

$n$	$P\left(\left|\overline{X}-\mu \right|\le \frac{1}{2}\sigma \right)$
1	38.29%
4	68.27%
16	95.45%
25	98.76%
49	99.96%

2. 总体服从任意分布时的样本均值分布

若总体服从期望为 $\mu$ ,方差为 ${\sigma }^2$ 的任意分布,则随机变量 $\overline{X}$ 也近似服从参数为 $\mu$ 和 ${\sigma }^2/n$ 的正态分布. 该结论基于中心极限定理.

16.3.3.3 均值的置信限

1. 方差 ${\sigma }^2$ 已知时,均值的置信区间

如果 $X$ 是参数为 $\mu$ 和 ${\sigma }^2$ 的随机变量,则根据 $16.3.3.2,\overline{X}$ 近似为参数是 $\mu$ 和 ${\sigma }^2/n$ 的正态随机变量,则通过变量替换

$$\begin{array}{}\text{(16.134)}& \overline{Z}=\frac{\overline{X}-\mu }{\sigma }\sqrt{n}\end{array}$$

可生成近似服从标准正态分布的随机变量 $\overline{Z}$ ,因此

$$\begin{array}{}\text{(16.135)}& P\left(\left|\overline{Z}\right|\le \epsilon \right)={\int }_{-\mathrm{\infty }}^{\epsilon }\phi \left(x\right)\mathrm{d}x=2\mathrm{\Phi }\left(\epsilon \right)-1.\end{array}$$

若给定显著性水平 $\alpha$ ,即

$$\begin{array}{}\text{(16.136)}& P\left(\left|\overline{Z}\right|\le \epsilon \right)=1-\alpha \end{array}$$

成立,则 $\epsilon =\epsilon \left(\alpha \right)$ 可由 (16.135) 确定,比如,对于标准正态分布,则可由 1458 页表 21.17 得到. 由 $\left|\overline{Z}\right|\le \epsilon \left(\alpha \right)$ 和 (16.134),可得关系式

$$\begin{array}{}\text{(16.137)}& \mu =\overline{x}\pm \frac{\sigma }{\sqrt{n}}\epsilon \left(\alpha \right)\end{array}$$

成立. (16.137) 中数值 $\overline{x}\pm \frac{\sigma }{\sqrt{n}}\epsilon \left(\alpha \right)$ 称为期望的置信限,二者之间的区间称为期望值 $\mu$ 的置信区间,其中方差 ${\sigma }^2$ 已知,给定显著性水平为 $\alpha$ . 换言之,期望值 $\mu$ 以概率 $1-\alpha$ 位于 (16.137) 的置信限之间.

注 若样本容量足够大,则 $s^2$ 可用来代替 (16.137) 中的 ${\sigma }^2$ . 当 $n>100$ 时可视为大样本,但实际应用时,要视具体问题而定,当 $n>30$ 时也可视为样本充分大. 若 $n$ 不是足够大,则在正态总体分布情形下,运用 $t$ 分布确定置信限,见(16.140).

2. 方差 ${\sigma }^2$ 未知时,期望的置信区间

若总体近似服从正态分布,且方差 ${\sigma }^2$ 未知,则在 (16.134) 中用样本方差 $s^2$ 代替 ${\sigma }^2$ ,可得随机变量

$$\begin{array}{}\text{(16.138)}& T=\frac{\overline{X}-\mu }{s}\sqrt{n}\end{array}$$

该变量服从自由度为 $m=n-1$ 的 $t$ 分布 (参见第 1076 页 16.2.4.8),其中 $n$ 是样本容量. 若 $n$ 很大,比如 $n>100$ ,则 $T$ 可视为正态随机变量,如同 (16.134) 中的 $Z$ . 对于给定的显著性水平 $\alpha$ ,有

$$\begin{array}{}\text{(16.139)}& P\left(\left|T\right|\le \epsilon \right)={\int }_{-\epsilon }^{\epsilon }{f}_t\left(x\right)\mathrm{d}x=P\left(\frac{|\overline{X}-\mu |}{s}\sqrt{n}\le \epsilon \right)=1-\alpha .\end{array}$$

由 (16.139) 可得 $\epsilon =\epsilon \left(\alpha ,n\right)=t_{\alpha /2;n-1}$ ,其中 $t_{\alpha /2;n-1}$ 是显著性水平为 $\alpha$ 的 $t$ 分布 (自由度为 $n-1$ ) 的分位数 (参见第 1463 页表 21.20). 由 $\left|T\right|=t_{\alpha /2;n-1}$ ,可推出

$$\begin{array}{}\text{(16.140)}& \mu =\overline{x}\pm \frac{s}{\sqrt{n}}{t}_{\alpha /2;n-1},\end{array}$$

数值 $\overline{x}\pm \frac{s}{\sqrt{n}}{t}_{\alpha /2;n-1}$ 称为总体方差 ${\sigma }^2$ 未知、显著性水平为 $\alpha$ 时期望值的置信限, 位于置信限之间的区间称为置信区间.

一组样本包含下述 6 个测量数据:0.842,0.846,0.835,0.839,0.843,0.838,可得到 $\overline{x}=0.8405$ 和 $s=0.00394$ .

若给定显著性水平 $\alpha$ 为 $5\mathrm{\%}$ 或 $1\mathrm{\%}$ ,那么,样本均值 $\overline{x}$ 和总体分布期望 $\mu$ 的最大偏差是多少?

(1) $\alpha =0.05$ : 查 1463 页表 21.20 可知 $t_{\alpha /2;5}=2.57$ ,因此 $\left|\overline{X}-\mu \right|\le 2.57$ . $0.00394/\sqrt{6}=0.0042$ . 故样本均值 $\overline{x}=0.8405$ 和期望值 $\mu$ 之差以 $95\mathrm{\%}$ 的可能性小于 $\pm 0.0042$ .

(2) $\alpha =0.01:t_{\alpha /2;5}=4.03,\left|\overline{X}-\mu \right|\le 4.03\cdot 0.00394/\sqrt{6}=0.0065$ ,即样本均值 $\overline{x}$ 和 $\mu$ 之差以 $99\mathrm{\%}$ 的可能性小于 $\pm 0.0065$ .

16.3.3.4 方差的置信区间

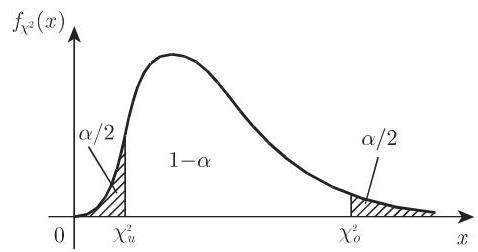
若随机变量 $X$ 服从参数为 $\mu$ 和 ${\sigma }^2$ 的正态分布,则随机变量

$$\begin{array}{}\text{(16.141)}& {\chi }^2=\left(n-1\right)\frac{s^2}{{\sigma }^2}\end{array}$$

服从自由度为 $m=n-1$ 的 ${\chi }^2$ 分布,其中 $n$ 是样本容量, $s^2$ 是样本方差. $f_{{\chi }^2}\left(x\right)$ 表示 ${\chi }^2$ 分布的密度函数,见图 16.15. 由图可知

$$\begin{array}{}\text{(16.142)}& P\left({\chi }^2<{\chi }_u^2\right)=P\left({\chi }^2>{\chi }_o^2\right)=\frac{\alpha }{2}.\end{array}$$

于是,由 ${\chi }^2$ 分布的分位数表 (参见第 1460 页表 21.18) 可给出

$$\begin{array}{}\text{(16.143)}& {\chi }_u^2={\chi }_{1-\alpha /2;n-1}^2,{\chi }_o^2={\chi }_{\alpha /2;n-1}^2.\end{array}$$

根据 (16.141) 可推出,当显著性水平为 $\alpha$ 时,总体未知方差 ${\sigma }^2$ 的估计值:

$$\begin{array}{}\text{(16.144)}& \frac{\left(n-1\right)s^2}{{\chi }_{\alpha /2;n-1}^2}\le {\sigma }^2\le \frac{\left(n-1\right)s^2}{{\chi }_{1-\alpha /2;n-1}^2}.\end{array}$$

对于小样本,(16.144) 所给出的 ${\sigma }^2$ 的置信区间相当大.

$◼$ 对于有 6 个测量数据的数值实例 (见上页),当 $\alpha =5\mathrm{\%}$ 时,由 1460 页表 21.18 可得到 ${\chi }_{0.025;5}^2=0.831,{\chi }_{0.975;5}^2=12.8$ ,故由(16.144)可推出 $0.625\cdot s\le \sigma \le$ $2.453\cdot s$ ,且 $s=0.00394$ .

16.3.3.5 假设检验的结构

统计学上的假设检验具有下述结构:

(1) 首先,要对样本来自于具有某种特定性质的总体作出假设 $H$ . 例如,

$H$ : 总体服从参数为 $\mu$ 和 ${\sigma }^2$ 的正态分布 (或其他已知分布),或者

$H$ : 对于未知的 $\mu$ ,可通过插入近似值 (估计值) ${\mu }_0$ 来得到,比如通过样本均值 $\overline{x}$ 四舍五入得到. 或者

$H$ : 两个总体的期望相同,即 ${\mu }_1-{\mu }_2=0$ 等.

(2) 以假设 $H$ 为基础,确定置信区间 $B$ (通常用表格给出). 样本函数值应以给定概率落在该区间内,如当 $\alpha =0.01$ 时,以 $99\mathrm{\%}$ 的概率落在该区间内.

(3) 计算样本函数值. 若函数值落在给定区间 $B$ 内,则接受假设,否则,拒绝该假设.

• 给定显著性水平 $\alpha$ ,检验假设 $H:\mu ={\mu }_0$ .

根据第 1093 页 16.3.3.3,随机变量 $T=\frac{\overline{X}-{\mu }_0}{s}\sqrt{n}$ 服从自由度为 $m=n-1$ 的 $t$ 分布,由此可推出,如果 $\overline{x}$ 未落入 (16.140) 定义的置信区间,即若

$$\begin{array}{}\text{(16.145)}& \left|\overline{X}-{\mu }_0\right|\ge \frac{s}{\sqrt{n}}{t}_{\alpha /2;n-1}\end{array}$$

成立, 则拒绝该假设. 此时可称存在显著性差异, 对假设检验的深入探讨参见 [16.24].