Appearance
2.19.2 网络算图
为了表示由方程
给出的各变量间的对应关系 (在很多情况下,可直接表示成
注 (1) 通过改变标度, 算图法也能用于其他区域, 例如, 若图 2.108 中的定义域变为
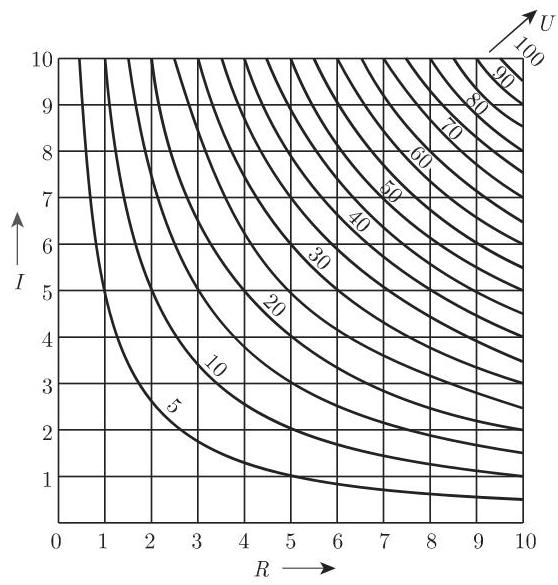
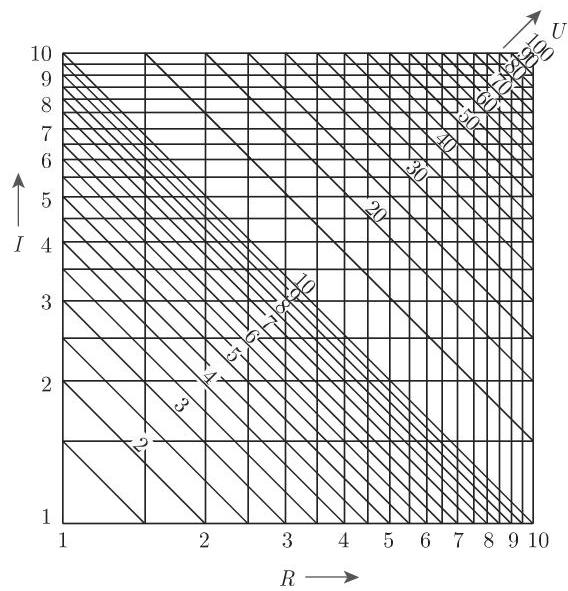
(2) 利用标度 (参见第 149 页 2.17.1) 有可能把复杂曲线的算图转换成直线算图. 如利用
的方程都能表示成由直线组成的算图. 若利用函数标度
的方程能够表示为平行于坐标轴的两族曲线和任意一族直线.
Appearance
为了表示由方程
给出的各变量间的对应关系 (在很多情况下,可直接表示成
注 (1) 通过改变标度, 算图法也能用于其他区域, 例如, 若图 2.108 中的定义域变为

(2) 利用标度 (参见第 149 页 2.17.1) 有可能把复杂曲线的算图转换成直线算图. 如利用
的方程都能表示成由直线组成的算图. 若利用函数标度
的方程能够表示为平行于坐标轴的两族曲线和任意一族直线.
