13.1.1 一个标量变量的向量函数

13.1.1.1 定义

1. 一个标量变量 $t$ 的向量函数

一个标量变量 $t$ 的向量函数是一个向量 $\overrightarrow{a}$ ,其分量是 $t$ 的实函数:

$$\begin{array}{}\text{(13.1)}& \overrightarrow{a}=\overrightarrow{a}\left(t\right)=a_x\left(t\right){\overrightarrow{e}}_x+a_y\left(t\right){\overrightarrow{e}}_y+a_z\left(t\right){\overrightarrow{e}}_z.\end{array}$$

对向量 $\overrightarrow{a}\left(t\right)$ ,可按分量地定义其极限、连续性、可微性等概念.

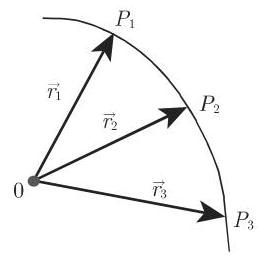
2. 向量函数的速端曲线

把向量函数 $\overrightarrow{a}\left(t\right)$ 视作点 $P$ 的位置或径向量 $\overrightarrow{r}=\overrightarrow{r}\left(t\right)$ ,则当 $t$ 变化时,这个函数就描绘了一条空间曲线 (图 13.1). 这条空间曲线被称为向量函数 $\overrightarrow{a}\left(t\right)$ 的速端曲线(hodograph).

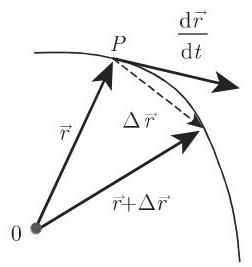
13.1.1.2 向量函数的导数

(13.1) 关于 $t$ 的导数也是 $t$ 的一个向量函数:

$$\begin{array}{}\text{(13.2)}& \frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{\overrightarrow{a}\left(t+\mathrm{\Delta }t\right)-\overrightarrow{a}\left(t\right)}{\mathrm{\Delta }t}=\frac{\mathrm{d}{a}_x\left(t\right)}{\mathrm{d}t}{\overrightarrow{e}}_x+\frac{\mathrm{d}{a}_y\left(t\right)}{\mathrm{d}t}{\overrightarrow{e}}_y+\frac{\mathrm{d}{a}_z\left(t\right)}{\mathrm{d}t}{\overrightarrow{e}}_z.\end{array}$$

径向量的导数 $\frac{\mathrm{d}\overrightarrow{r}}{\mathrm{d}t}$ 的几何描述是在 $P$ 点处的一个指向速端曲线切线方向的向量 (图 13.2). 其长度依赖于参数 $t$ 的选取. 如果 $t$ 是时间,则 $\overrightarrow{r}\left(t\right)$ 描述点 $P$ 在空间的运动 (所述空间曲线是其路径),而 $\frac{\mathrm{d}\overrightarrow{r}}{\mathrm{d}t}$ 具有这个运动的方向和大小. 如果 $t=s$ 是从某点开始度量的这条空间曲线的弧长,则显然有 $\left|\frac{\mathrm{d}\overrightarrow{r}}{\mathrm{d}s}\right|=1$ .

13.1.1.3 向量的微分法则

$$\begin{array}{}\text{(13.3a)}& \frac{\mathrm{d}}{\mathrm{d}t}\left(\overrightarrow{a}\pm \overrightarrow{b}\pm \overrightarrow{c}\right)=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}\pm \frac{\mathrm{d}\overrightarrow{b}}{\mathrm{d}t}\pm \frac{\mathrm{d}\overrightarrow{c}}{\mathrm{d}t},\end{array}$$$$\begin{array}{}\text{(13.3b)}& \frac{\mathrm{d}}{\mathrm{d}t}\left(\phi \overrightarrow{a}\right)=\frac{\mathrm{d}\phi }{\mathrm{d}t}\overrightarrow{a}+\phi \frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}\left(\phi \text{ 是 }t\text{ 的一个标量函数 }\right),\end{array}$$$$\begin{array}{}\text{(13.3c)}& \frac{\mathrm{d}}{\mathrm{d}t}\left(\overrightarrow{a}\overrightarrow{b}\right)=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}\overrightarrow{b}+\overrightarrow{a}\frac{\mathrm{d}\overrightarrow{b}}{\mathrm{d}t}\end{array}$$$$\begin{array}{}\text{(13.3d)}& \frac{\mathrm{d}}{\mathrm{d}t}\left(\overrightarrow{a}\times \overrightarrow{b}\right)=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}\times \overrightarrow{b}+\overrightarrow{a}\times \frac{\mathrm{d}\overrightarrow{b}}{\mathrm{d}t}\text{(因子不必可交换),}\end{array}$$$$\begin{array}{}\text{(13.3e)}& \frac{\mathrm{d}}{\mathrm{d}t}\overrightarrow{a}\left[\phi \left(t\right)\right]=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}\phi }\cdot \frac{\mathrm{d}\phi }{\mathrm{d}t}\text{ (链规则). }\end{array}$$

如果 $\left|\overrightarrow{a}\left(t\right)\right|=$ 常数,即 ${\overrightarrow{a}}^2\left(t\right)=\overrightarrow{a}\left(t\right)\cdot \overrightarrow{a}\left(t\right)=$ 常数,则从 (13.3c) 即得 $\overrightarrow{a}\cdot \frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}=0$ ,即 $\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}$ 和 $\overrightarrow{a}$ 相互垂直. 这个事实的例子如下:

$◼\mathbf{A}$:平面中一个圆周的径向量和切向量；

$◼\mathbf{B}$: 球面上一条曲线的位置向量和切向量. 此时, 速端曲线是一条球面曲线.

13.1.1.4 向量函数的泰勒展开

$$\begin{array}{}\text{(13.4)}& \overrightarrow{a}\left(t+h\right)=\overrightarrow{a}\left(t\right)+h\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}+\frac{h^2}{2!}\frac{{\mathrm{d}}^2\overrightarrow{a}}{\mathrm{d}{t}^2}+\cdots +\frac{h^n}{n!}\frac{{\mathrm{d}}^n\overrightarrow{a}}{\mathrm{d}{t}^n}+\cdots .\end{array}$$

一个向量函数用泰勒级数的展开只是在该级数收敛时才有意义. 因为极限是按分量来定义的, 因此收敛性可以按分量来验证, 所以具有向量项的这个级数的收敛性可以用与具有复数项级数的收敛性 (参见第 980 页 14.3.2) 完全一样的方法来确定. 因而具有向量项的一个级数的收敛性被归结为具有标量项的级数的收敛性. 一个向量函数 $\overrightarrow{a}\left(t\right)$ 的微分由下式定义:

$$\begin{array}{}\text{(13.5)}& \mathrm{d}\overrightarrow{a}=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t}\mathrm{\Delta }t.\end{array}$$