Appearance
2.16.2 实用的经验公式
本节讨论经验函数相关性的一些简单情形, 并给出相应的图示. 每个图示都给出几条与公式中不同参数值相对应的曲线, 在随后几节中讨论参数对曲线形状的影响.
为了选择恰当的函数, 必须考虑其对应的图像, 以便再现经验数据. 例如, 我们不能仅在经验数据曲线有极大或极小值时判断公式
2.16.2.1 幂函数
1.
图 2.80 给出了当幂函数
的指数
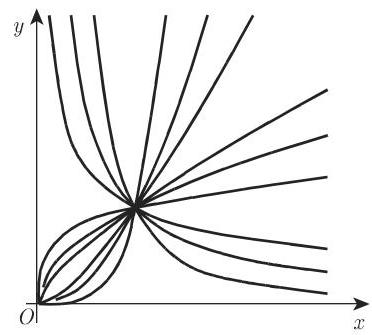
2.
公式
所表示的曲线与 (2.255a) 类似,但要在
若
为了确定
在确定出
2.16.2.2 指数函数
1.
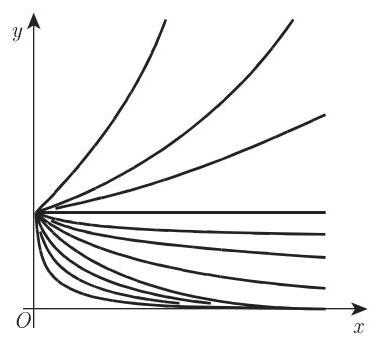
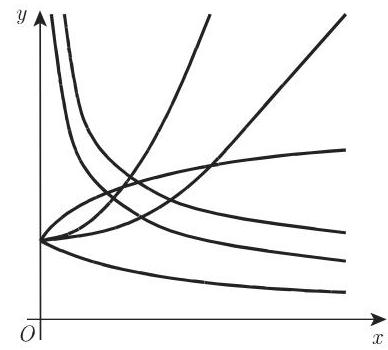
图 2.81 给出了函数
的曲线图形. 92 页 2.6.1 中讨论了指数函数(2.54) 和它的图像 (图 2.26). 可进行如下修正
2.
公式
所表示的曲线与 (2.257a) 相同,但要在
为了确定像 (2.256d) 中那样的
2.16.2.3 二次多项式
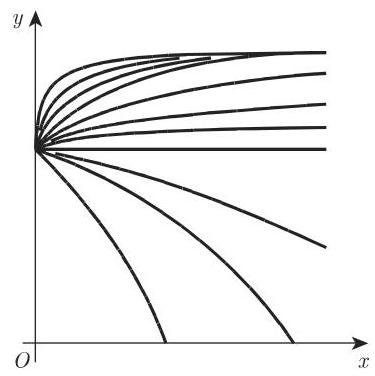
图 2.84 给出了二次多项式
的所有可能的曲线形状. 关于二次多项式 (2.41) 及其曲线图示 2.12 的讨论见 82 页 2.3.2. 通常利用最小二乘法可确定出系数
若给定的
在这两种情况中, 由方程
确定出
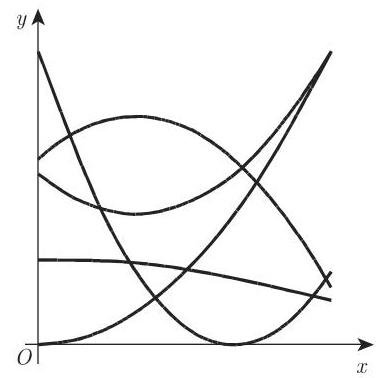
2.16.2.4 有理线性函数
第 85 页 2.4 中 (2.46) 和图 2.17(参见第 86 页) 已讨论了有理线性函数:
对任一数据点
有时有理线性函数不是 (2.260a) 的形式, 而是满足 (2.260d)
在前一情况下可做修正
2.16.2.5 二次多项式的平方根
方程
可能表示的曲线形状如图 2.85 所示. 91 页中已讨论过函数 (2.52) 及其图像 (图 2.23). 若引进新的变量
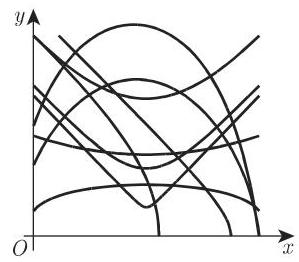
2.16.2.6 一般误差曲线
函数
的典型曲线图像如图 2.86 所示. 方程 (2.61) 和图 2.30
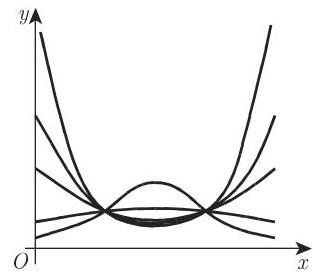
若引进新的变量
2.16.2.7 第 II 类三次曲线
函数
的所有可能形状如图 2.87 所示, 方程 (2.48) 和图 2.19 曾讨论过该函数 (参见第 87 88 页).
若引进新的变量
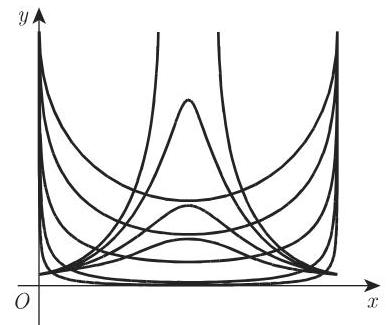
2.16.2.8 第 III 类三次曲线
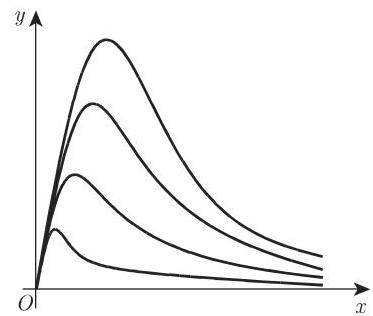
函数
的典型曲线形状如图 2.88 所示,方程 (2.49) 和图 2.20 讨论过该函数 (参见 88~89 页).
①原文中为图 2.31, 译者认为, 应订正为图 2.30.——译者注
若引进新的变量
2.16.2.9 第 I 类三次曲线
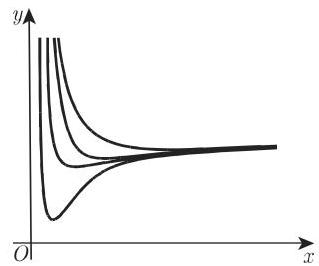
函数
的典型曲线形状如图 2.89 所示,方程 (2.47) 和图 2.18 讨论过该函数 (参见第 86~87 页).
若引进新的变量
2.16.2.10 幂函数和指数函数的乘积
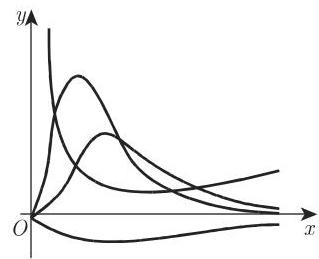
函数
的典型曲线形状如图 2.90 所示, 方程 (2.62) 和图 2.31 讨论过该函数 (参见第 96~97 页).
若
做修正. 其中
做修正.
若
2.16.2.11 指数和
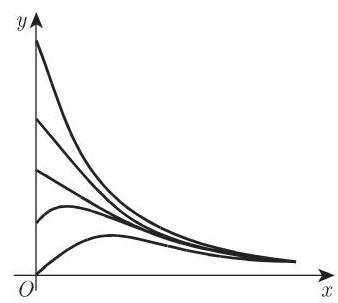
指数和
的典型曲线形状如图 2.91 所示. 方程 (2.60) 和图 2.29 讨论过该函数 (参见第 94~95 页).
若
可再次进行修正.
2.16.2.12 数值算例
根据表 2.9 中给定的
0.1 | 1.78 | 0.056 | 0.007 | -1.000 | 0.250 | 0.301 | 0.252 | 0.252 | 1.78 |
0.2 | 3.18 | 0.063 | 0.031 | -0.699 | 0.502 | 0.176 | +0.002 | -0.097 | 3.15 |
0.3 | 3.19 | 0.094 | 0.063 | -0.523 | 0.504 | 0.125 | -0.099 | -0.447 | 3.16 |
0.4 | 2.54 | 0.157 | 0.125 | -0.398 | 0.405 | 0.097 | -0.157 | -0.803 | 2.52 |
0.5 | 1.77 | 0.282 | 0.244 | -0.301 | 0.248 | 0.079 | -0.191 | -1.134 | 1.76 |
0.6 | 1.14 | 0.526 | 0.488 | -0.222 | 0.057 | 0.067 | -0.218 | -1.455 | 1.14 |
0.7 | 0.69 | 1.014 | 0.986 | -0.155 | -0.161 | 0.058 | -0.237 | 0.70 | |
0.8 | 0.40 | 2.000 | 1.913 | -0.097 | -0.398 | 0.051 | -0.240 | 0.41 | |
0.9 | 0.23 | 3.913 | 3.78 | -0.046 | -0.638 | 0.046 | -0.248 | 0.23 | |
1.0 | 0.13 | 7.69 | 8.02 | 0.000 | -0.886 | 0.041 | -0.269 | 0.13 | |
1.1 | 0.07 | 15.71 | 14.29 | 0.041 | -1.155 | 0.038 | -0.243 | 0.07 | |
1.2 | 0.04 | 30.0 | 0.079 | -1.398 | 0.04 |
选择近似函数 首先画出由这些给定的数据所表示的图像 (图 2.92), 通过把该图像与前面讨论的曲线进行对比, 可以看到图 2.88 和图 2.90 中曲线所刻画的函数 (2.264) 或 (2.266a) 符合目前研究的这种类型.
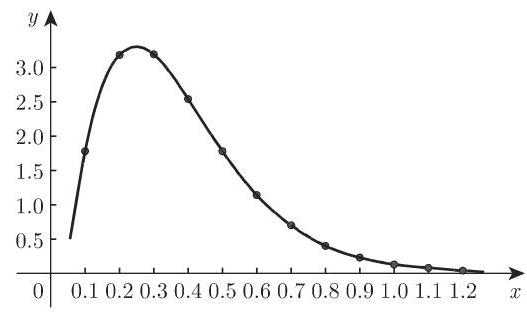
确定参数 利用公式 (2.264) 做修正
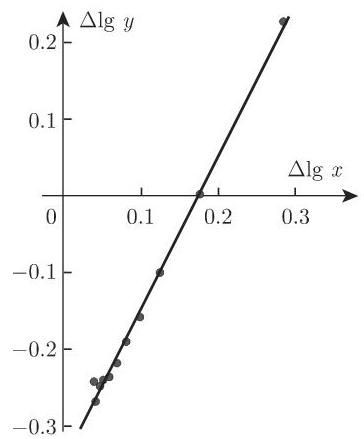
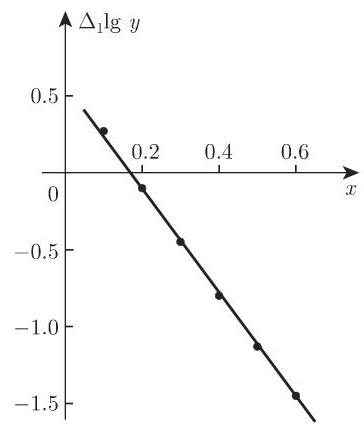
为了确定常数
由此得到
由经过修正所确定的参数作为非线性最小二乘问题 (参见第 1282 页 19.6.2.4) 迭代解的初始值
得到