15.4.1 $Z$ 变换的性质

15.4.1.1 离散函数

若仅知函数 $f\left(t\right)\left(0\le t<\mathrm{\infty }\right)$ 在自变量离散点 $t_n=nT(n=0,1,2,\cdots ;T>0$ 是常数) 处的取值,则可记作 $f\left(nT\right)=f_n$ ,且构成序列 $\left\{f_n\right\}$ . 比如,在电工学中,在离散时间段 $t_n$ 处 “浏览” 函数 $f\left(t\right)$ ,即可产生这样的序列. 其表达式为阶梯函数 (图 15.27).

只在自变量离散点处有定义的函数 $f\left(nT\right)$ (称为离散函数) 和序列 $\left\{f_n\right\}$ ,二者是等价的.

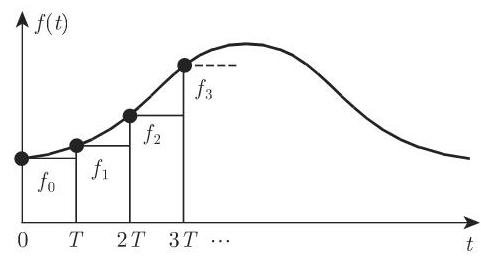
15.4.1.2 $Z$ 变换的定义

1. 原序列和变换

给定序列 $\left\{f_n\right\}$ ,可得到无穷级数

$$\begin{array}{}\text{(15.105)}& F\left(z\right)=\sum _{n=0}^{\mathrm{\infty }}{f}_n{\left(\frac{1}{z}\right)}^n.\end{array}$$

若该级数收敛,则序列 $\left\{f_n\right\}$ 称为可 $Z$ 变换的,且可表示为

$$\begin{array}{}\text{(15.106)}& F\left(z\right)=\mathcal{Z}\left\{f_n\right\}.\end{array}$$

$\left\{f_n\right\}$ 称为原序列, $F\left(z\right)$ 称为变换函数, $z$ 表示复变量, $F\left(z\right)$ 是复值函数.

$◼f_n=1\left(n=0,1,2,\cdots \right)$ . 对应的无穷级数是

$$\begin{array}{}\text{(15.107)}& F\left(z\right)=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{1}{z}\right)}^n.\end{array}$$

它表示公比为 $1/z$ 的几何级数,当 $\left|\frac{1}{z}\right|<1$ 时,级数收敛,其和是 $F\left(z\right)=\frac{z}{z-1}$ . 当 $\left|\frac{1}{z}\right|\ge 1$ 时,级数发散. 因此,当 $\left|\frac{1}{z}\right|<1$ 时,即对于 $z$ 平面内单位圆 $\left|z\right|=1$ 的任何外点,序列 $\{1\}$ 是可 $Z$ 变换的.

2. 性质

根据式 (15.105),变换 $F\left(z\right)$ 是复变量 $1/z$ 的幂级数,由复幂级数 (参见第 979 页 14.3.1.3) 的性质, 可知如下结论:

a) 对于可 $Z$ 变换的序列 $\left\{f_n\right\}$ ,存在实数 $R$ ,使得当 $\left|z\right|>1/R$ 时,级数 (15.105) 绝对收敛,当 $\left|z\right|<1/R$ 时,级数发散. 当 $\left|z\right|\ge 1/R_0>1/R$ 时,级数一致收敛. $R$ 是关于 $1/z$ 的幂级数 (15.105) 的收敛半径. 若对于任意 $\left|z\right|>0$ ,级数收敛,则 $R=\mathrm{\infty }$ . 对于不可 $Z$ 变换的序列,有 $R=0$ .

b) 若当 $\left|z\right|>1/R$ 时, $\left\{f_n\right\}$ 是可 $Z$ 变换的,则当 $\left|z\right|>1/R$ 时,对应的变换 $F\left(z\right)$ 是解析函数,且它是 $\left\{f_n\right\}$ 的唯一变换. 反之,若当 $\left|z\right|>1/R$ 时, $F\left(z\right)$ 是解析函数,且在 $z=\mathrm{\infty }$ 处, $F\left(z\right)$ 是正则的,则对于 $F\left(z\right)$ ,存在唯一的原序列 $\left\{f_n\right\}$ . 若 $F\left(z\right)$ 有形如 (15.105) 的幂级数展开式,且 $F\left(\mathrm{\infty }\right)=f_0$ ,则称 $F\left(z\right)$ 在 $z=\mathrm{\infty }$ 处是正则的.

3. 极限定理

与拉普拉斯变换的极限性质类似 (参见第 1006 页 (15.7b)),对于 $Z$ 变换有下述极限定理成立.

a) 若 $F\left(z\right)=\mathcal{Z}\left\{f_n\right\}$ 存在,则

$$\begin{array}{}\text{(15.108)}& f_0=\underset{z\to \mathrm{\infty }}{lim}F\left(z\right).\end{array}$$

此处, $z$ 可以沿着实轴或其他任何路径趋向于无穷大. 由于级数

$$\begin{array}{}\text{(15.109)}& z\left\{F\left(z\right)-f_0\right\}=f_1+f_2\frac{1}{z}+f_3\frac{1}{z^2}+\cdots ,\end{array}$$$$\begin{array}{}\text{(15.110)}& z^2\left\{F\left(z\right)-f_0-f_1\frac{1}{z}\right\}=f_2+f_3\frac{1}{z}+f_4\frac{1}{z^2}+\cdots ,\end{array}$$$$⋮$$

明显是 $Z$ 变换,类似于式 (15.108),可得到

$$\begin{array}{}\text{(15.111)}& f_1=\underset{z\to \mathrm{\infty }}{lim}z\left\{F\left(z\right)-f_0\right\},f_2=\underset{z\to \mathrm{\infty }}{lim}{z}^2\left\{F\left(z\right)-f_0-f_1\frac{1}{z}\right\},\cdots .\end{array}$$

通过这种方式,原序列 $\left\{f_n\right\}$ 可根据其变换 $F\left(z\right)$ 来确定.

b) 若 $\underset{n\to \mathrm{\infty }}{lim}{f}_n$ 存在,则

$$\begin{array}{}\text{(15.112)}& \underset{n\to \mathrm{\infty }}{lim}{f}_n=\underset{z\to 1+0}{lim}\left(z-1\right)F\left(z\right).\end{array}$$

但由于上述命题不可逆,根据式 (15.112),只有能保证 $\underset{n\to \mathrm{\infty }}{lim}{f}_n$ 存在时,才能确定其值.

$◼f_n={(-1)}^n\left(n=0,1,2,\cdots \right)$ ,则 $\mathcal{Z}\left\{f_n\right\}=\frac{z}{z+1}$ ,且 $\underset{z\to 1+0}{lim}\left(z-1\right)\frac{z}{z+1}=0$ ,但 $\underset{n\to \mathrm{\infty }}{lim}{(-1)}^n$ 不存在.

15.4.1.3 计算法则

在运用 $Z$ 变换时,了解定义在原序列上的某些运算对变换的影响及其反过来的情况,是很重要的. 此处为了简化,当 $\left|z\right|>1/R$ 时,将使用记号 $F\left(z\right)=\mathcal{Z}\left\{f_n\right\}$ .

1. 平移

需要区分向前平移和向后平移.

(1) 第一移位定理: $\mathcal{Z}\left\{f_{n-k}\right\}=z^{-k}F\left(z\right)\left(k=0,1,2,\cdots \right)$ .(15.113)

当 $n-k<0$ 时,定义 $f_{n-k}=0$ .

(2) 第二移位定理: $\mathcal{Z}\left\{f_{n+k}\right\}=z^k\left[F\left(z\right)-\sum _{v=0}^{k-1}{f}_v{\left(\frac{1}{z}\right)}^v\right]\left(k=1,2,\cdots \right)$ .(15.114)

2. 求和

当 $\left|z\right|>max\left(1,\frac{1}{R}\right)$ 时,有 $\mathcal{Z}\left\{\sum _{v=0}^{n-1}{f}_v\right\}=\frac{1}{z-1}F\left(z\right)$ .(15.115)

3. 差分

对于差分

$$\mathrm{\Delta }{f}_n=f_{n+1}-f_n,{\mathrm{\Delta }}^m{f}_n=\mathrm{\Delta }\left({\mathrm{\Delta }}^{m-1}{f}_n\right)\left(m=1,2,\cdots ;{\mathrm{\Delta }}^0{f}_n=f_n\right)$$

(15.116)

有下述等式成立:

$$\mathcal{Z}\left\{\mathrm{\Delta }{f}_n\right\}=\left(z-1\right)F\left(z\right)-z{f}_0,$$$$\mathcal{Z}\left\{{\mathrm{\Delta }}^2{f}_n\right\}={(z-1)}^{2}F\left(z\right)-z\left(z-1\right)f_0-z{f}_0,$$$$\begin{array}{}\text{(15.117)}& ⋮\end{array}$$$$\mathcal{Z}\left\{{\mathrm{\Delta }}^k{f}_n\right\}={(z-1)}^{k}F\left(z\right)-z\sum _{v=0}^{k-1}{(z-1)}^{k-v-1}{\mathrm{\Delta }}^v{f}_0.$$

4. 阻尼

对于任意复数 $\lambda \ne 0$ 和 $\left|z\right|>\frac{\left|\lambda \right|}{R}$ ,有

$$\begin{array}{}\text{(15.118)}& \mathcal{Z}\left\{{\lambda }^n{f}_n\right\}=F\left(\frac{z}{\lambda }\right).\end{array}$$

5. 卷积

两个序列 $\left\{f_n\right\}$ 和 $\left\{g_n\right\}$ 的卷积是运算

$$\begin{array}{}\text{(15.119)}& f_n\ast g_n=\sum _{v=0}^n{f}_v{g}_{n-v}.\end{array}$$

若当 $\left|z\right|>1/R_1$ 时, $z$ 变换函数 $\mathcal{Z}\left\{f_n\right\}=F\left(z\right)$ ,以及当 $\left|z\right|>1/R_2$ 时, $\mathcal{Z}\left\{g_n\right\}=G\left(z\right)$ 存在,则对于 $\left|z\right|>max\left(\frac{1}{R_1},\frac{1}{R_2}\right)$ ,有

$$\begin{array}{}\text{(15.120)}& \mathcal{Z}\left\{f_n\ast g_n\right\}=F\left(z\right)G\left(z\right).\end{array}$$

关系式 (15.120) 称为 $Z$ 变换的卷积定理. 它相当于两个幂级数的乘法法则.

6. 变换的微分

$$\begin{array}{}\text{(15.121)}& \mathcal{Z}\left\{n{f}_n\right\}=-z\frac{\mathrm{d}F\left(z\right)}{\mathrm{d}z}.\end{array}$$

重复运用 (15.121),可得到 $F\left(z\right)$ 的高阶导数.

7. 变换的积分

当假定 $f_0=0$ 时,有

$$\begin{array}{}\text{(15.122)}& \mathcal{Z}\left\{\frac{f_n}{n}\right\}={\int }_z^{\mathrm{\infty }}\frac{F\left(\xi \right)}{\xi }\mathrm{d}\xi .\end{array}$$

15.4.1.4 与拉普拉斯变换的关系

把离散函数 $f\left(t\right)$ (参见第 1038 页 15.4.1.1) 描述为阶梯函数,则

$f\left(t\right)=f\left(nT\right)=f_n,$ 其中, $nT\le t<\left(n+1\right)T\left(n=0,1,2,\cdots ;T>0,T\text{ 是常数 }\right),$(15.123)

对于该分段常数函数,求拉普拉斯变换 (参见第 1006 页 15.2.1.1,1.),当 $T=1$ 时, 有

$$\mathcal{L}\{f\left(t\right)\}=F\left(p\right)=\sum _{n=0}^{\mathrm{\infty }}{\int }_n^{n+1}{f}_n{\mathrm{e}}^{-pt}\mathrm{d}t$$$$\begin{array}{}\text{(15.124)}& =\sum _{n=0}^{\mathrm{\infty }}{f}_n\frac{{\mathrm{e}}^{-np}-{\mathrm{e}}^{-\left(n+1\right)p}}{p}=\frac{1-{\mathrm{e}}^{-p}}{p}\sum _{n=0}^{\mathrm{\infty }}{f}_n{\mathrm{e}}^{-np}.\end{array}$$

(15.124) 中的无穷级数称为离散拉普拉斯变换,用 $\mathcal{D}$ 表示:

$$\begin{array}{}\text{(15.125)}& \mathcal{D}\{f\left(t\right)\}=\mathcal{D}\left\{f_n\right\}=\sum _{n=0}^{\mathrm{\infty }}{f}_n{\mathrm{e}}^{-np}.\end{array}$$

在式 (15.125) 中进行 ${\mathrm{e}}^p=z$ 的替换后, $\mathcal{D}\left\{f_n\right\}$ 表示关于 $1/z$ 的幂级数,即所谓的洛朗级数(参见第 981 页 14.3.4). 替换 ${\mathrm{e}}^p=z$ 启示了 $Z$ 变换的名称. 根据该变换, 由式 (15.124),可最终得到,在阶梯函数的情况下,拉普拉斯变换和 $Z$ 变换之间有下述关系:

$$\begin{array}{}\text{(15.126a)}& pF\left(p\right)=\left(1-\frac{1}{z}\right)F\left(z\right)\end{array}$$

或

$$\begin{array}{}\text{(15.126b)}& p\mathcal{L}\{f\left(t\right)\}=\left(1-\frac{1}{z}\right)\mathcal{Z}\left\{f_n\right\}.\end{array}$$

通过这种方式,阶梯函数的 $Z$ 变换 (参见第 1454 页表 21.15) 可转化为阶梯函数的拉普拉斯变换 (参见第 1431 页表 21.13), 反之亦然.

15.4.1.5 $Z$ 变换的逆变换

$Z$ 变换的逆变换是根据变换 $F\left(z\right)$ ,探寻对应的唯一原序列 $\left\{f_n\right\}$ :

$$\begin{array}{}\text{(15.127)}& {\mathcal{Z}}^{-1}\{F\left(z\right)\}=\left\{f_n\right\}.\end{array}$$

求逆变换有不同的方法.

1. 使用表格

若表格中没有给出函数 $F\left(z\right)$ ,则我们可试着把 $F\left(z\right)$ 转化为表 21.15 中已给出的函数.

2. $F\left(z\right)$ 的洛朗级数

若关于 $1/z$ 的 $F\left(z\right)$ 的级数展开式已知或可求出,则使用第 1039 页定义 (15.105), 可直接求其逆变换.

3. $F\left(\frac{1}{z}\right)$ 的泰勒级数

由于 $F\left(\frac{1}{z}\right)$ 是关于 $z$ 的幂递增的级数,根据 (15.105),使用泰勒公式,可推出

$$\begin{array}{}\text{(15.128)}& f_n={\frac{1}{n!}\frac{{\mathrm{d}}^n}{\mathrm{d}{z}^n}F\left(\frac{1}{z}\right)|}_{z=0}\left(n=0,1,2,\cdots \right).\end{array}$$

4. 极限定理的应用

使用第 1040 页的极限式 (15.108) 和 (15.111),原序列 $\left\{f_n\right\}$ 可由其变换 $F\left(z\right)$ 直接确定.

$◼F\left(z\right)=\frac{2z}{\left(z-2\right){(z-1)}^2}.$

使用上述四种方法:

(1) 对 $F\left(z\right)/z$ 进行部分分式分解 (参见第 18 页 1.1.7.3),可生成表 21.15 中包含的函数.

$$\frac{F\left(z\right)}{z}=\frac{2}{\left(z-2\right){(z-1)}^2}=\frac{A}{z-2}+\frac{B}{{(z-1)}^2}+\frac{C}{z-1}.$$

故

$$F\left(z\right)=\frac{2z}{z-2}-\frac{2z}{{(z-1)}^2}-\frac{2z}{z-1}.$$

因此,当 $n\ge 0$ 时, $f_n=2\left(2^n-n-1\right)$ .

(2) 展开 $F\left(z\right)$ ,可得到关于 $z$ 的幂递减的级数:

$$\begin{array}{}\text{(15.129)}& F\left(z\right)=\frac{2z}{z^3-4z^2+5z-2}=2\frac{1}{z^2}+8\frac{1}{z^3}+22\frac{1}{z^4}+52\frac{1}{z^5}+114\frac{1}{z^6}+\cdots .\end{array}$$

由此表达式可得 $f_0=f_1=0,f_2=2,f_3=8,f_4=22,f_5=52,f_6=114,\cdots$ , 但对于一般项 $f_n$ ,无法得到一个闭合表达式.

(3) 对于公式 $F\left(\frac{1}{z}\right)$ 及其需要求出的导数 (见 (15.128)),建议考虑 $F\left(z\right)$ 的部

分分式分解:

$$\begin{array}{cccc}F\left(\frac{1}{z}\right)=\frac{2}{1-2z}-\frac{2z}{{(1-z)}^2}-\frac{2}{1-z},& \text{ 即 }& F\left(\frac{1}{z}\right)=0,& \text{ 对于 }z=0\\ \frac{\mathrm{d}F\left(\frac{1}{z}\right)}{\mathrm{d}z}=\frac{4}{{(1-2z)}^2}-\frac{4z}{{(1-z)}^3}-\frac{4}{{(1-z)}^2},& \text{ 即 }& \frac{\mathrm{d}F\left(\frac{1}{z}\right)}{\mathrm{d}z}=0,& \text{ 对于 }z=0\\ \frac{{\mathrm{d}}^{2}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^2}=\frac{16}{{(1-2z)}^3}-\frac{12z}{{(1-z)}^4}-\frac{12}{{(1-z)}^3},& \text{ 即 }& \frac{{\mathrm{d}}^{2}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^2}=4,& \text{ 对于 }z=0\\ \frac{{\mathrm{d}}^{3}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^3}=\frac{96}{{(1-2z)}^4}-\frac{48z}{{(1-z)}^5}-\frac{48}{{(1-z)}^4},& \text{ 即 }& \frac{{\mathrm{d}}^{3}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^3}=48,& \text{ 对于 }z=0\\ \frac{{\mathrm{d}}^{3}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^3}=\frac{96}{{(1-z)}^4}-\frac{48+8z}{{(1-z)}^5},& \text{ 则 }& \frac{{\mathrm{d}}^{3}F\left(\frac{1}{z}\right)}{\mathrm{d}{z}^3}=48,& \text{ 对于 }z=0\end{array}\}$$

(15.130)

由此,根据式 (15.128),容易得到 $f_0,f_1,f_2,f_3,\cdots$ .

(4) 运用极限定理 (参见第 1040 页 15.4.1.2, 3.), 可给出:

$$\begin{array}{}\text{(15.131a)}& f_0=\underset{z\to \mathrm{\infty }}{lim}F\left(z\right)=\underset{z\to \mathrm{\infty }}{lim}\frac{2z}{z^3-4z^2+5z-2}=0,\end{array}$$$$\begin{array}{}\text{(15.131b)}& f_1=\underset{z\to \mathrm{\infty }}{lim}z\left(F\left(z\right)-f_0\right)=\underset{z\to \mathrm{\infty }}{lim}\frac{2z^2}{z^3-4z^2+5z-2}=0,\end{array}$$$$\begin{array}{}\text{(15.131c)}& f_2=\underset{z\to \mathrm{\infty }}{lim}{z}^2\left(F\left(z\right)-f_0-f_1\frac{1}{z}\right)=\underset{z\to \mathrm{\infty }}{lim}\frac{2z^3}{z^3-4z^2+5z-2}=2,\end{array}$$$$f_3=\underset{z\to \mathrm{\infty }}{lim}{z}^3\left(F\left(z\right)-f_0-f_1\frac{1}{z}-f_2\frac{1}{z^2}\right)$$$$\begin{array}{}\text{(15.131d)}& =\underset{z\to \mathrm{\infty }}{lim}{z}^3\left(\frac{2z}{z^3-4z^2+5z-2}-\frac{2}{z^2}\right)=8,\cdots ,\end{array}$$

其中运用了伯努利-洛必达法则(参见第 72 页 2.1.4.8,2.). 可依次求出原序列 $\left\{f_n\right\}$ .