19.6.2 平均逼近

平均逼近的原理是高斯最小二乘法. 在计算中, 区别连续与离散两种情况.

19.6.2.1 连续问题、正规方程

函数 $f\left(x\right)$ 被区间 $\left[a,b\right]$ 上的函数 $g\left(x\right)$ 近似,使得依赖于 $g\left(x\right)$ 所包含的参数的表达式

$$\begin{array}{}\text{(19.169)}& F={\int }_a^b\omega \left(x\right){[f\left(x\right)-g\left(x\right)]}^2\mathrm{d}x\end{array}$$

取极小值. $\omega \left(x\right)$ 表示给定的权函数,且在积分区间上 $\omega \left(x\right)>0$ .

设最佳逼近 $g\left(x\right)$ 有如下形式:

$$\begin{array}{}\text{(19.170)}& g\left(x\right)=\sum _{i=0}^n{a}_i{g}_i\left(x\right),\end{array}$$

其中函数 $g_0\left(x\right),g_1\left(x\right),\cdots ,g_n\left(x\right)$ 线性无关,则 (19.169) 取极值的必要条件为

$$\begin{array}{}\text{(19.171)}& \frac{\partial F}{\partial a_i}=0\left(i=0,1,\cdots ,n\right).\end{array}$$

由此得到所谓正规方程组

$$\begin{array}{}\text{(19.172)}& \sum _{i=0}^n{a}_i\left(g_i,g_k\right)=\left(f,g_k\right)\left(k=0,1,\cdots ,n\right)\end{array}$$

以确定未知系数 $a_i$ . 这里记号

$$\begin{array}{}\text{(19.173a)}& \left(g_i,g_k\right)={\int }_a^b\omega \left(x\right)g_i\left(x\right)g_k\left(x\right)\mathrm{d}x,\end{array}$$$$\begin{array}{}\text{(19.173b)}& \left(f,g_k\right)={\int }_a^b\omega \left(x\right)f\left(x\right)g_k\left(x\right)\mathrm{d}x\left(i,k=0,1,\cdots ,n\right)\end{array}$$

看作两个指示函数的内积.

因为函数 $g_0\left(x\right),g_1\left(x\right),\cdots ,g_n\left(x\right)$ 线性无关,故正规方程组有唯一解. 方程组 (19.172) 的系数矩阵是对称的, 故可用楚列斯基方法 (参见第 1245 页 19.2.1.2). 若函数组 $g_i\left(x\right)$ 是正交的,即若

$$\begin{array}{}\text{(19.174)}& \left(g_i,g_k\right)=0,i\ne k,\end{array}$$

则不用求解方程组就可直接确定系数 $a_i$ . 若

$$\begin{array}{}\text{(19.175)}& \left(g_i,g_k\right)=\{\begin{array}{ll}0,& i\ne k,\\ 1,& i=k\end{array}\left(i,k=0,1,\cdots ,n\right),\end{array}$$

称方程组为正交的. 满足 (19.175) 的正规方程 (19.172) 简化为

$$\begin{array}{}\text{(19.176)}& a_i=\left(f,g_i\right)\left(i=0,1,\cdots ,n\right).\end{array}$$

线性无关函数组可以正交化. 依赖于权函数和积分区间,从幂函数 $g_i\left(x\right)=x^i(i=$ $0,1,\cdots ,n)$ 得到表 19.2 中的正交多项式.(19.177)

$\left[a,b\right]$	$\omega \left(x\right)$	多项式名称	见页码
$\left[-1,1\right]$	1	勒让德多项式 $P_n\left(x\right)$	566
$\left[-1,1\right]$	$\frac{1}{\sqrt{1-x^2}}$	切比雪夫多项式 $T_n\left(x\right)$	989
$[0,\mathrm{\infty })$	${\mathrm{e}}^{-x}$	拉盖尔多项式 $L_n\left(x\right)$	568
$\left(-\mathrm{\infty },\mathrm{\infty }\right)$	${\mathrm{e}}^{-x^2/2}$	埃尔米特多项式 $H_n\left(x\right)$	568

这些多项式可在任意区间上应用.

(1) 有限近似区间.

(2)一端无限的近似区间, 如在依赖于时间的问题中.

(3) 两端都是无限的近似区间, 如在流问题中.

每个有限区间 $\left[a,b\right]$ 可通过变换

$$\begin{array}{}\text{(19.178)}& x=\frac{b+a}{2}+\frac{b-a}{2}t\left(x\in \left[a,b\right],t\in \left[-1,1\right]\right)\end{array}$$

化为区间 $\left[-1,1\right]$ .

19.6.2.2 离散问题、正规方程、豪斯霍尔德方法

设 $\left(x_v,y_v\right)$ 为 $N$ 对给定的测量值. 为了确定函数 $g\left(x\right)$ ,使其值 $g\left(x_v\right)$ 与给定值 $y_v$ 之差的平方表达式

$$\begin{array}{}\text{(19.179)}& F=\sum _{\nu =1}^N{[y_{\nu }-g\left(x_{\nu }\right)]}^2\end{array}$$

为极小. $F$ 的值依赖于包含在函数 $g\left(x\right)$ 中的参数. 公式 (19.179) 表示经典的残量平方和. 残量平方和的极小化称为最小二乘法. 从假设 (19.170) 和 (19.179) 对系数极小化的必要条件 $\frac{\partial F}{\partial a_i}=0\left(i=0,1,\cdots ,n\right)$ ,得到正规方程:

$$\begin{array}{}\text{(19.180)}& \sum _{i=0}^n{a}_i\left[g_i{g}_k\right]=\left[y{g}_k\right]\left(k=0,1,\cdots ,n\right).\end{array}$$

在下面的记号中用到高斯求和符号:

$$\begin{array}{}\text{(19.181a)}& \left[g_i{g}_k\right]=\sum _{\nu =1}^N{g}_i\left(x_{\nu }\right)g_k\left(x_{\nu }\right),\end{array}$$$$\begin{array}{}\text{(19.181b)}& \left[y{g}_k\right]=\sum _{\nu =1}^N{y}_{\nu }{g}_k\left(x_{\nu }\right)\left(i,k=0,1,\cdots ,n\right).\end{array}$$

通常 $n\ll N$ .

• 对多项式 $g\left(x\right)=a_0+a_{1}x+\cdots +a_n{x}^n$ ,正规方程为 $a_0\left[x^k\right]+a_1\left[x^{k+1}\right]+$ $\cdots +a_n\left[x^{k+n}\right]=\left[x^{k}y\right]\left(k=0,1,\cdots ,n\right)$ ,其中 $\left[x^k\right]=\sum _{v=1}^N{x}_v^k,\left[x^0\right]=N,\left[x^{k}y\right]=$ $\sum _{v=1}^N{x}_v^k{y}_v,\left[y\right]=\sum _{v=1}^N{y}_v$ . 正规方程 (19.180) 的系数矩阵是对称的,可以用楚列斯基方法数值求解.

正规方程 (19.180) 和残量平方和 (19.179) 有如下紧形式:

$$\begin{array}{}\text{(19.182a)}& {\mathbf{G}}^{\mathrm{T}}\mathbf{G}\underset{―}{\mathbf{a}}={\mathbf{G}}^{\mathrm{T}}\underset{―}{\mathbf{y}},F={(\underset{―}{\mathbf{y}}-\mathbf{G}\underset{―}{\mathbf{a}})}^{\mathrm{T}}\left(\underset{―}{\mathbf{y}}-\mathbf{G}\underset{―}{\mathbf{a}}\right),\end{array}$$

其中

$$\mathbf{G}=\left(\begin{array}{ccccc}{g}_0\left(x_1\right)& g_1\left(x_1\right)& g_2\left(x_1\right)& \cdots & g_n\left(x_1\right)\\ g_0\left(x_2\right)& g_1\left(x_2\right)& g_2\left(x_2\right)& \cdots & g_n\left(x_2\right)\\ g_0\left(x_3\right)& g_1\left(x_3\right)& g_2\left(x_3\right)& \cdots & g_n\left(x_3\right)\\ ⋮& ⋮& ⋮& & ⋮\\ g_0\left(x_N\right)& g_1\left(x_N\right)& g_2\left(x_N\right)& \cdots & g_n\left(x_N\right)\end{array}\right),$$$$\begin{array}{}\text{(19.182b)}& \underset{―}{\mathbf{y}}=\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\\ ⋮\\ y_N\end{array}\right),\underset{―}{\mathbf{a}}=\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_m\end{array}\right).\end{array}$$

若以求解 $N$ 点 $\left(x_{\nu },y_{\nu }\right)$ 的插值问题,代替求解残量和的极小化,则需求解如下方程组:

$$\begin{array}{}\text{(19.183)}& G\underset{―}{a}=\underset{―}{y}.\end{array}$$

若 $n<N-1$ ,则方程组超定,通常无任何解. 方程组 (19.180) 或 (19.182a) 可由 (19.183) 乘以 ${\mathbf{G}}^{\mathrm{T}}$ 得到.

从数值角度看, 推荐用豪斯霍尔德方法 (参见第 420 页 4.5.3.2, 2.) 解方程 (19.183), 其解导致极小的残量平方和 (19.179).

19.6.2.3 多维问题

1. 调整计算

设函数 $f\left(x_1,x_2,\cdots ,x_n\right)$ 有 $n$ 个独立变量 $x_1,x_2,\cdots ,x_n$ . 其显形式未知,仅给出 $N$ 个通常为测量值的代入值 $f_{\nu }$ . 这些数值记在下表中 (见 (19.184)).(19.184)

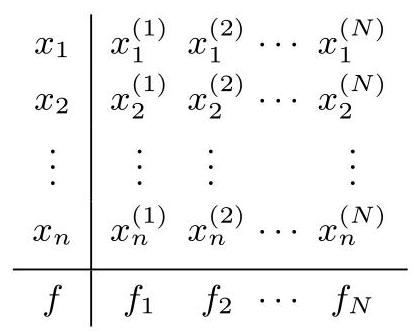
通过引进下列向量可更清晰地给出调整问题:

$\underset{―}{\mathbf{x}}={(x_1,x_2,\cdots ,x_n)}^{\mathrm{T}}$ : 有 $n$ 个独立变量的向量,

${\underset{―}{x}}^{\left(\nu \right)}={(x_1^{\left(\nu \right)},x_2^{\left(\nu \right)},\cdots ,x_n^{\left(\nu \right)})}^{\mathrm{T}}$ : 第 $\nu$ 个插值点的向量 $\left(\nu =1,\cdots ,N\right)$ ,

$\underset{―}{f}={(f_1,f_2,\cdots ,f_N)}^{\mathrm{T}}$ : 在 $N$ 个插值点的 $N$ 个函数值向量.

$f\left(x_1,x_2,\cdots ,x_n\right)=f\left(\underset{―}{\mathbf{x}}\right)$ 由形如

$$\begin{array}{}\text{(19.185)}& g\left(x_1,x_2,\cdots ,x_n\right)=\sum _{i=0}^m{a}_i{g}_i\left(x_1,x_2,\cdots ,x_n\right)\end{array}$$

的函数近似. 这里 $g_i\left(x_1,x_2,\cdots ,x_n\right)=g_i\left(\underset{―}{x}\right)$ 是 $m+1$ 个适当选取的函数.

$◼\mathbf{A}$: $n$ 变量的线性近似 $g_i\left(x_1,x_2,\cdots ,x_n\right)=a_0+a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n$ .

$◼\mathbf{B}$: 三变量的完全二次近似

$$g\left(x_1,x_2,x_3\right)=a_0+a_1{x}_1+a_2{x}_2+a_3{x}_3+a_4{x}_1^2+a_5{x}_2^2$$$$+a_6{x}_3^2+a_7{x}_1{x}_2+a_8{x}_1{x}_3+a_9{x}_2{x}_3.$$

系数由极小化 $\sum _{\nu =1}^N{[f_{\nu }-g(x_1^{\left(c\right)},x_2^{\left(c\right)},\cdots ,x_n^{\left(c\right)})]}^2$ 选定.

2. 正规方程组

把插值点 $x_{\nu }$ 换为向量插值点 ${\underset{―}{x}}^{\left(\nu \right)}\left(\nu =1,2,\cdots ,N\right)$ ,类似于(19.182b)构造矩阵 $\mathbf{G}$ . 为确定系数,可以用正规方程组

$$\begin{array}{}\text{(19.186)}& {\mathbf{G}}^{\mathrm{T}}\mathbf{G}\underset{―}{\mathbf{a}}={\mathbf{G}}^{\mathrm{T}}\underset{―}{\mathbf{f}}\end{array}$$

或超定的方程组

$$\begin{array}{}\text{(19.187)}& G\underset{―}{a}=\underset{―}{f}.\end{array}$$

$◼$ 对于多维回归的例子参见第 1099 页 16.3.4.3,3.

19.6.2.4 非线性最小二乘问题

对一维离散问题讨论其主要思想. 近似函数 $g\left(x\right)$ 非线性依赖于某些参数.

$◼\mathbf{A}$: $g\left(x\right)=a_0{\mathrm{e}}^{a_{1}x}+a_2{\mathrm{e}}^{a_{3}x}$ ,该表达式并非线性依赖于参数 $a_1,a_3$ .

$◼\mathbf{B}$: $g\left(x\right)=a_0{\mathrm{e}}^{a_{1}x}+\cos a_{2}x$ ,该函数并非线性依赖于参数 $a_1,a_2$ .

记号

$$\begin{array}{}\text{(19.188)}& g=g\left(x,\underset{―}{\mathbf{a}}\right)=g\left(x;a_0,a_1,\cdots ,a_n\right)\end{array}$$

指出了近似函数 $g\left(x\right)$ 依赖于参数向量 $\underset{―}{\mathbf{a}}={(a_0,a_1,\cdots ,a_n)}^{\mathrm{T}}$ 的事实. 假设给定 $N$ 对数值 $\left(x_{\nu },y_{\nu }\right)\left(\nu =1,2,\cdots ,N\right)$ . 极小化残量平方和

$$\begin{array}{}\text{(19.189)}& \sum _{\nu =1}^N{[y_{\nu }-g(x_{\nu };a_0,a_1,\cdots ,a_n)]}^2=F\left(a_0,a_1,\cdots ,a_n\right),\end{array}$$

由必要条件 $\frac{\partial F}{\partial a_i}=0\left(i=0,1,\cdots ,n\right)$ 得到非线性正规方程组,必须用迭代法,例如牛顿法 (参见第 1250 页 19.2.2.2) 求解.

在实际问题中常用的求解此问题的另一途径是为解非线性最小二乘问题 (19.24) 而给出的高斯-牛顿法 (参见第 1251 页 19.2.2.3). 下面的步骤用来解非线性逼近问题 (19.189):

(1) 借助关于 $a_i$ 的泰勒公式线性化近似函数 $g\left(x,\underset{―}{\mathbf{a}}\right)$ . 为此,需要近似值 $a_i^{\left(0\right)}$ $\left(i=0,1,\cdots ,n\right)$ :

$$\begin{array}{}\text{(19.190)}& g\left(x,\underset{―}{\mathbf{a}}\right)\approx \tilde{g}\left(x,\underset{―}{\mathbf{a}}\right)=g\left(x,{\underset{―}{\mathbf{a}}}^{\left(0\right)}\right)+\sum _{i=0}^n\frac{\partial g}{\partial a_i}\left(x,{\underset{―}{\mathbf{a}}}^{\left(0\right)}\right)\left(a_i-a_i^{\left(0\right)}\right).\end{array}$$

(2) 借助正规方程组

$$\begin{array}{}\text{(19.191)}& {\tilde{\mathbf{G}}}^{\mathrm{T}}\tilde{\mathbf{G}}\underset{―}{\mathrm{\Delta }a}={\tilde{\mathbf{G}}}^{\mathrm{T}}\underset{―}{\mathrm{\Delta }y}\end{array}$$

或豪斯霍尔德方法, 求解线性极小化问题

$$\begin{array}{}\text{(19.192)}& \sum _{\nu =1}^N{[y_{\nu }-\tilde{g}(x_{\nu },\underset{―}{\mathbf{a}})]}^2=min!\end{array}$$

在 (19.191) 中向量 $\underset{―}{a}$ 和 $\underset{―}{y}$ 的分量由下式给出:

$$\begin{array}{}\text{(19.193a)}& \mathrm{\Delta }{a}_i=a_i-a_i^{\left(0\right)}\left(i=0,1,2,\cdots ,n\right),\end{array}$$$$\begin{array}{}\text{(19.193b)}& \mathrm{\Delta }{y}_{\nu }=y_{\nu }-g\left(x_{\nu },{\underset{―}{\mathbf{a}}}^{\left(0\right)}\right)\left(\nu =1,2,\cdots ,N\right).\end{array}$$

可类似于 (19.182b) 中的 $\mathbf{G}$ 确定矩阵 $\tilde{\mathbf{G}}$ ,其中 $g_i\left(x_v\right)$ 换为

$$\frac{\partial g}{\partial a_i}\left(x_{\nu },{\underset{―}{\mathbf{a}}}^{\left(0\right)}\right)\left(i=0,1,\cdots ,n;\nu =1,2,\cdots ,N\right).$$

(3) 计算新的近似

$$\begin{array}{}\text{(19.194)}& a_i^{\left(1\right)}=a_i^{\left(0\right)}+\mathrm{\Delta }{a}_i\text{ 或 }{a}_i^{\left(1\right)}=a_i^{\left(0\right)}+\gamma \mathrm{\Delta }{a}_i\left(i=0,1,2,\cdots ,n\right),\end{array}$$

其中 $\gamma >0$ 为步长参数.

用 $a_i^{\left(1\right)}$ 代替 $a_i^{\left(0\right)}$ 重复步骤 2 和步骤 3,等等,得到要求参数的一列近似值,其收敛性强烈依赖于初始近似的精度. 残量的平方和的值可由引入乘子 $\gamma$ 得到.