5.8.3 树和生成树

5.8.3.1 树

1. 树

一个没有圈的无向连通图称为树. 每个至少有 2 个顶点的树至少有 2 个次数为 1 的顶点. 每个有 $n$ 个顶点的树恰有 $n-1$ 条边.

如果有向图 $G$ 连通,并且不含任何环道,那么称它为树 (参见第 551 页 5.8.6). 图 5.49 和图 5.50 表示两个不同构的有 14 个顶点的树. 它们表示丁烷和异构丁烷的化学结构.

2. 有根树

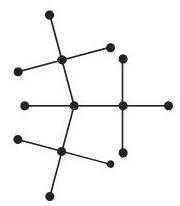
具有一个特异顶点的树称作有根树, 并且这个特异顶点称作根. 在图示中, 根通常在顶部, 并且各边位于根的下方 (图 5.51). 有根树用来表示等级结构, 例如, 工厂中设备的等级、系谱图、语法结构.

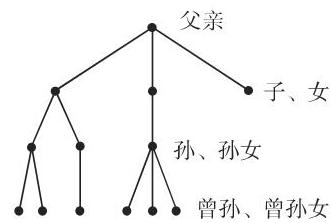
图 5.51 用有根树表示一个家庭的谱系. 根是表示父亲的顶点.

3. 正则二元树

如果一个树恰有一个 2 次顶点且不然仅有 1 次或 3 次顶点, 那么称它为正则二元树.

正则二元树的顶点个数是奇数. 具有 $n$ 个顶点的正则树有 $\left(n+1\right)/2$ 个 1 次顶点. 一个顶点的水平是指根到它的距离. 树中出现的最大水平称为树的高. 正则二元有根树 (例如在信息科学中) 有若干应用.

4. 有序二元树

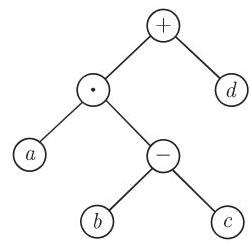
算术表达式可以通过二元树表示. 在此, 数和变量被指派为 1 次顶点, 运算 “+”、“-” 和 “.” 对应于次数 $>1$ 的顶点,并且左边的子树和右边的子树分别表示第一和第二运算对象, 一般地这也是一个表达式. 这些树称为有序二元树.

遍历一个有序二元树可以用三种不同的方法实施, 它们是用递推方式定义的 (还见图 5.52):

内序遍历: 遍历根的左子树 (按内序遍历方式) 抵达根,

遍历根的右子树 (按内序遍历方式).

前序遍历: 抵达根,

遍历根的左子树 (按前序遍历方式),

遍历根的右子树 (按前序遍历方式).

后序遍历: 遍历根的左子树 (按后序遍历方式),

遍历根的右子树 (按后序遍历方式),

抵达根.

应用内序遍历, 与给定表达式对照, 项的顺序是不变的. 用后序遍历得到的项称为后缀表示法或波兰(Polish) 表示法. 类似地, 用前序遍历得到的项称为前缀表示法或逆波兰表示法.

前缀表示法和后缀表示法唯一地刻画一个树. 这个事实可以用于树的实现.

在图 5.52 中项 $a\cdot \left(b-c\right)+d$ 是用图表示的. 内序遍历产生 $a\cdot b-c+d$ ,前序遍历产生 $+\cdot a-bcd$ ,后序遍历产生 $abc-\cdot d+$ .

5.8.3.2 生成树

1. 生成树

如果一个树是无向图 $G$ 的子图,并且含有 $G$ 的所有顶点,那么称它为 $G$ 的生成树. 每个有限连通图 $G$ 含有一个生成树 $H$ :

如果 $G$ 含有一个圈,那么去掉这个圈的一条边. 剩余的图 $G_1$ 仍然是连通的并且又可以通过去掉 $G_1$ 的一个圈的一条边 (如果存在这样的边). 经过有限多步后就可得到 $G$ 的生成树.

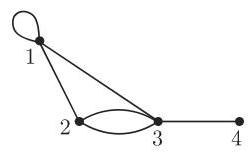
图 5.54 给出图 5.53 中的图 $G$ 的生成树 $H$ .

2. 凯莱定理

每个有 $n$ 个顶点 $\left(n>1\right)$ 的完全图恰有 $n^{n-2}$ 个生成树.

3. 矩阵生成树定理

设 $G=\left(V,E\right)$ 是一个图,其中 $V=\left\{v_1,v_2,\cdots ,v_n\right\}\left(n>1\right)$ 以及 $E=$ $\left\{e_1,e_2,\cdots ,e_m\right\}$ . 定义(n, n)型的矩阵 $\mathbf{D}=\left(d_{ij}\right)$ :

$$\begin{array}{}\text{(5.323a)}& d_{ij}=\{\begin{array}{ll}0,& i\ne j,\\ d_G\left(v_i\right),& i=j,\end{array}\end{array}$$

称它为次数矩阵. 次数矩阵和邻接矩阵的差是 $G$ 的容许矩阵 $\mathbf{L}$ :

$$\begin{array}{}\text{(5.323b)}& \mathbf{L}=\mathbf{D}-\mathbf{A}.\end{array}$$

去掉 $\mathbf{L}$ 的第 $i$ 行和第 $i$ 列,得到矩阵 ${\mathbf{L}}_i.{\mathbf{L}}_i$ 的行列式等于图 $G$ 的生成树的个数. 图 5.53 中的图的邻接矩阵、次数矩阵和容许矩阵是

$$\mathbf{A}=\left(\begin{array}{llll}2& 1& 1& 0\\ 1& 0& 2& 0\\ 1& 2& 0& 1\\ 0& 0& 1& 0\end{array}\right),\mathbf{D}=\left(\begin{array}{llll}4& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& 4& 0\\ 0& 0& 0& 1\end{array}\right),\mathbf{L}=\left(\begin{array}{cccc}2& -1& -1& 0\\ -1& 3& -2& 0\\ -1& -2& 4& -1\\ 0& 0& -1& 1\end{array}\right).$$

因为 $det{\mathbf{L}}_3=5$ ,所以这个图有 5 个生成树.

4. 极小生成树

设 $G=\left(V,E,f\right)$ 是一个连通加权图. 如果 $G$ 的生成树 $H$ 的总长

$$\begin{array}{}\text{(5.324)}& f\left(H\right)=\sum _{e\in H}f\left(e\right)\end{array}$$

极小,那么 $H$ 称为极小生成树. 例如,如果边权表示成本,并且我们关心极小成本, 那么就要搜索极小生成树. 一个求极小生成树的方法是克鲁斯卡尔 (Kruskal) 算法:

a) 选取有极小权的边.

b) 尽可能地继续选取其他的有最小权, 并且不与已经选得的边形成圈的边, 将这样的边添加到树中.

在步骤 $\mathrm{b})$ 中,容许边的选取容易通过下列标号算法实现:

• 设图的顶点被两两不同地标号.

• 在每一步, 仅可能在这种情形增加一条边: 它连接有不同标号的顶点.

• 增加一条边后, 将较大标号端点的标号改为较小的端点标号值.