8.2.5 由级数展开式进行积分、特殊非初等函数

即使被积函数为初等函数, 其积分也不一定总能由初等函数来表示, 在很多情况下可以用级数展开式来表示这些非初等积分. 若被积函数可以展成区间 $\left[a,b\right]$ 上一致收敛的级数,则通过逐项积分也可得到积分 ${\int }_a^{x}f\left(t\right)\mathrm{d}t$ 的一致收敛级数.

1. 正弦积分 $\left(\left|x\right|<\mathrm{\infty }\text{,也可参见第 987 页 14.4.3.2,2.}\right)$

$$\mathrm{Si}\left(x\right)={\int }_0^x\frac{\sin t}{t}\mathrm{d}t=\frac{\pi }{2}-{\int }_x^{\mathrm{\infty }}\frac{\sin t}{t}\mathrm{d}t$$$$\begin{array}{}\text{(8.95)}& =x-\frac{x^3}{3\cdot 3!}+\frac{x^5}{5\cdot 5!}-+\cdots +\frac{{(-1)}^n{x}^{2n+1}}{\left(2n+1\right)\cdot \left(2n+1\right)!}+\cdots .\end{array}$$

2. 余弦积分 $\left(0<x<\mathrm{\infty }\right)$

$$\mathrm{Ci}\left(x\right)=-{\int }_x^{\mathrm{\infty }}\frac{\cos t}{t}\mathrm{d}t=C+\ln x-{\int }_0^x\frac{1-\cos t}{t}\mathrm{d}t$$$$\begin{array}{}\text{(8.96a)}& =C+\ln x-\frac{x^2}{2\cdot 2!}+\frac{x^4}{4\cdot 4!}-+\cdots +\frac{{(-1)}^n{x}^{2n}}{2n\cdot \left(2n\right)!}+\cdots ,\end{array}$$

其中

$$\begin{array}{}\text{(8.96b)}& C=-{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-t}\ln t\mathrm{d}t=0.577215665\cdots .\text{(欧拉常数)}\end{array}$$

3. 对数积分 $(0<x<1$ ,当 $1<x<\mathrm{\infty }$ 时为柯西主值)

$$\begin{array}{}\text{(8.97)}& \mathrm{Li}\left(x\right)={\int }_0^x\frac{\mathrm{d}t}{\ln t}=C+\ln \left|\ln x\right|+\ln x+\frac{{(\ln x)}^2}{2\cdot 2!}+\cdots +\frac{{(\ln x)}^n}{n\cdot n!}+\cdots .\end{array}$$

4. 指数积分 $(-\mathrm{\infty }<x<0$ ,当 $0<x<\mathrm{\infty }$ 时为柯西主值)

$$\begin{array}{}\text{(8.98a)}& \mathrm{Ei}\left(x\right)={\int }_{-\mathrm{\infty }}^x\frac{{\mathrm{e}}^t}{t}\mathrm{d}t=C+\ln \left|x\right|+x+\frac{x^2}{2\cdot 2!}+\cdots +\frac{x^n}{n\cdot n!}+\cdots .\end{array}$$$$\begin{array}{}\text{(8.98b)}& \mathrm{Ei}\left(\ln x\right)=\mathrm{Li}\left(x\right).\end{array}$$

5. 高斯误差积分与误差函数

当 $\left|x\right|<\mathrm{\infty }$ 时可定义高斯误差积分,记为 $\varphi$ . 其具体定义和关系如下:

$$\begin{array}{}\text{(8.99a)}& \mathrm{\Phi }\left(x\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\mathrm{\infty }}^x{\mathrm{e}}^{-\frac{t^2}{2}}\mathrm{d}t,\end{array}$$$$\begin{array}{}\text{(8.99b)}& \underset{x\to \mathrm{\infty }}{lim}\mathrm{\Phi }\left(x\right)=1,\end{array}$$$$\begin{array}{}\text{(8.99c)}& {\mathrm{\Phi }}_0\left(x\right)=\frac{1}{\sqrt{2\pi }}{\int }_0^x{\mathrm{e}}^{-\frac{t^2}{2}}\mathrm{d}t=\mathrm{\Phi }\left(x\right)-\frac{1}{2}.\end{array}$$

函数 $\varphi \left(x\right)$ 是标准正态分布的分布函数 (参见第 1070 页 16.2.4.2),其值可通过查 1458 页的表 21.17 得到.

统计学中常常要用到误差函数 $\mathrm{erf}\left(x\right)$ (也可参见第 1070 页 16.2.4.2),此类函数与高斯误差积分存在密切关系:

$$\begin{array}{}\text{(8.100a)}& \mathrm{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{\mathrm{e}}^{-t^2}\mathrm{d}t=2{\mathrm{\Phi }}_0\left(x\sqrt{2}\right),\end{array}$$$$\begin{array}{}\text{(8.100b)}& \underset{x\to \mathrm{\infty }}{lim}\mathrm{erf}\left(x\right)=1\end{array}$$$$\mathrm{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}\left(x-\frac{x^3}{1!\cdot 3}+\frac{x^5}{2!\cdot 5}-+\cdots +\frac{{(-1)}^n{x}^{2n+1}}{n!\cdot \left(2n+1\right)}+\cdots \right),$$$$\begin{array}{}\text{(8.100d)}& {\int }_0^x\mathrm{erf}\left(t\right)\mathrm{d}t=x\mathrm{erf}\left(x\right)+\frac{1}{\sqrt{\pi }}\left({\mathrm{e}}^{-x^2}-1\right),\end{array}$$$$\begin{array}{}\text{(8.100e)}& \frac{\mathrm{derf}\left(x\right)}{\mathrm{d}x}=\frac{2}{\sqrt{\pi }}{\mathrm{e}}^{-x^2}.\end{array}$$

6. 伽马函数与阶乘

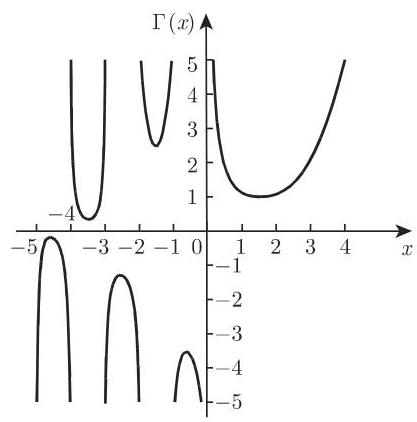
(1) 定义 伽马函数又称第二类欧拉积分 (8.91), 是除了 0 和负整数之外包含复数在内的任意数 $x$ 的阶乘的推广. 函数 $\mathrm{\Gamma }\left(x\right)$ 的曲线如图 8.23 所示,1426 页的表 21.10 给出了其取值. 伽马函数可由下面两种方式来定义:

$$\begin{array}{}\text{(8.101a)}& \mathrm{\Gamma }\left(x\right)={\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-t}{t}^{x-1}\mathrm{d}t\left(x>0\right)\text{ 或 }\end{array}$$$$\begin{array}{}\text{(8.101b)}& \mathrm{\Gamma }\left(x\right)=\underset{n\to \mathrm{\infty }}{lim}\frac{n^x\cdot n!}{x\left(x+1\right)\left(x+2\right)\cdots \left(x+n\right)}\left(x\ne 0,-1,-2,\cdots \right).\end{array}$$

(2)伽马函数的性质

$$\begin{array}{}\text{(8.102a)}& \mathrm{\Gamma }\left(x+1\right)=x\mathrm{\Gamma }\left(x\right),\end{array}$$$$\begin{array}{}\text{(8.102b)}& \mathrm{\Gamma }\left(n+1\right)=n!\left(n=0,1,2,\cdots \right),\end{array}$$$$\begin{array}{}\text{(8.102c)}& \mathrm{\Gamma }\left(x\right)\mathrm{\Gamma }\left(1-x\right)=\frac{\pi }{\sin \pi x}\left(x\ne 0,\pm 1,\pm 2,\cdots \right),\end{array}$$$$\begin{array}{}\text{(8.102d)}& \mathrm{\Gamma }\left(\frac{1}{2}\right)=2{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-t^2}\mathrm{d}t=\sqrt{\pi },\end{array}$$$$\begin{array}{}\text{(8.102e)}& \mathrm{\Gamma }\left(n+\frac{1}{2}\right)=\frac{\left(2n\right)!\sqrt{\pi }}{n!2^{2n}}\left(n=0,1,2,\cdots \right),\end{array}$$$$\begin{array}{}\text{(8.102f)}& \mathrm{\Gamma }\left(-n+\frac{1}{2}\right)=\frac{{(-1)}^{n}n!2^{2n}\sqrt{\pi }}{\left(2n\right)!}\left(n=0,1,2,\cdots \right).\end{array}$$

当自变量为复数 $z$ 时,只要实部 $\mathrm{Re}\left(z\right)>0$ ,公式 (8.102a) 和 (8.102c) 也成立.

(3) 阶乘概念的推广 当前阶乘的概念仅限于正整数 $n$ (参见第 15 页 1.1.6.4,3.), 现将它推广到任意实数, 可得函数

$$\begin{array}{}\text{(8.103a)}& x!=\mathrm{\Gamma }\left(x+1\right)\text{.}\end{array}$$

于是有下面等式成立:

当 $x$ 为正整数时: $x!=1\cdot 2\cdot 3\cdots x$ ,(8.103b)

若 $x=0:0!=\mathrm{\Gamma }\left(1\right)=1$ ,(8.103c)

当 $x$ 为负整数时: $x!=\pm \mathrm{\infty }$ ,(8.103d)

若 $x=\frac{1}{2}:\left(\frac{1}{2}\right)!=\mathrm{\Gamma }\left(\frac{3}{2}\right)=\frac{\sqrt{\pi }}{2}$ ,(8.103e)

若 $x=-\frac{1}{2}:\left(-\frac{1}{2}\right)!=\mathrm{\Gamma }\left(\frac{1}{2}\right)=\sqrt{\pi }$ ,(8.103f)

若 $x=-\frac{3}{2}:\left(-\frac{3}{2}\right)!=\mathrm{\Gamma }\left(-\frac{1}{2}\right)=-2\sqrt{\pi }$ .(8.103g)

当数 $n$ 大于 10 及 $n$ 为分数时,都可以用斯特林 (Stirling) 公式来近似确定它的阶乘:

$$\begin{array}{}\text{(8.103h)}& n!\approx {\left(\frac{n}{\mathrm{e}}\right)}^n\sqrt{2\pi n}\left(1+\frac{1}{12n}+\frac{1}{288n^2}+\cdots \right),\end{array}$$$$\begin{array}{}\text{(8.103i)}& \ln \left(n!\right)\approx \left(n+\frac{1}{2}\right)\ln n-n+\ln \sqrt{2\pi }.\end{array}$$

7. 椭圆积分

对完全椭圆积分 (参见第 654 页 8.1.4.3, 2.), 可采用下面的级数展开式

$$K={\int }_0^{\frac{\pi }{2}}\frac{\mathrm{d}\vartheta }{\sqrt{1-k^2{\sin }^2\vartheta }}$$$$\begin{array}{}\text{(8.104)}& =\frac{\pi }{2}\left[1+{\left(\frac{1}{2}\right)}^2{k}^2+{\left(\frac{1\cdot 3}{2\cdot 4}\right)}^2{k}^4+{\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)}^2{k}^6+\cdots \right],k^2<1,\end{array}$$$$E={\int }_0^{\frac{\pi }{2}}\sqrt{1-k^2{\sin }^2\vartheta }\mathrm{d}\vartheta$$$$\begin{array}{}\text{(8.105)}& =\frac{\pi }{2}\left[1-{\left(\frac{1}{2}\right)}^2\frac{k^2}{1}-{\left(\frac{1\cdot 3}{2\cdot 4}\right)}^2\frac{k^4}{3}-{\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)}^2\frac{k^6}{5}-\cdots \right],k^2<1.\end{array}$$

1424 页表 21.9 给出了椭圆积分的数值.