Appearance
8.3.1 第一类线积分
8.3.1.1 定义
第一类线积分或对弧长的积分是满足如下形式的定积分
其中
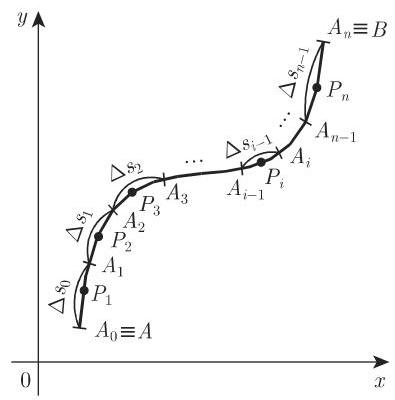
(1) 在可求长弧段
(2) 在每个小弧段
(3) 用函数在点
(4) 将
(5) 当
的极限,若无论
类似地, 可对积分路径为空间曲线弧段上的三元函数定义第一类线积分:
8.3.1.2 存在定理
设有一连续曲线弧段
8.3.1.3 第一类线积分的计算
为了计算第一类线积分, 可将其化为定积分.
1. 以参数形式给出的积分路径方程
若积分路径的方程为
当积分路径为空间曲线
其中
2. 以显形式
令
对于空间曲线情形, 由 (8.108b), 得
其中
8.3.1.4 第一类线积分的应用
表 8.6 列出了第一类线积分的一些应用. 表 8.7 列出了不同坐标系下计算线积分所用的曲线微元
曲线段 | |
质地不均匀的曲线段 | |
重心的坐标 | |
平面曲线在 | |
空间曲线关于坐标轴的 转动惯量 |
笛卡儿坐标 | ||
空间曲线 | 笛卡儿坐标系下的参数形式 |