15.1.6 积分变换的应用

1. 应用领域

积分变换除了在积分方程理论和线性算子理论等基础数学领域有重要理论意义外, 在物理学和工程学实际问题求解中也有广泛应用. 应用积分变换求解问题的方法通常称为算子方法, 适用于求解常微分方程、偏微分方程、积分方程和差分方程.

2. 算子方法的框架图

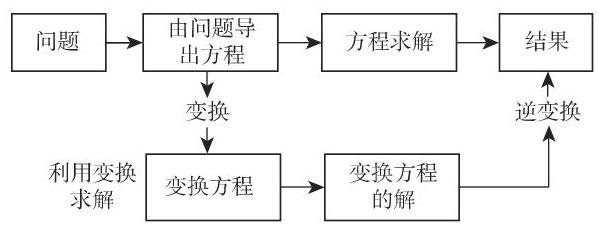
图 15.1 给出了运用积分变换算子方法的一般框架. 为了得到问题的解, 我们不直接求解初始定义方程, 而是首先应用积分变换把方程变为另一个方程, 然后求变换方程的解, 并应用逆变换给出初始问题的解.

运用算子方法求解常微分方程包括下述三个步骤:

(1)把关于未知函数的微分方程转化为其变换方程.

(2) 求变换方程在像空间的解. 变换方程通常不再是微分方程, 而是代数方程.

(3) 利用变换的逆变换 ${\mathcal{T}}^{-1}$ 回到原始空间,即确定初始问题的解.

算子方法的主要困难通常不是求解变换方程, 而在于求函数变换和逆变换.