3.3.3 多面体

在这一节中我们将使用以下记号: $V$ 为体积, $S$ 为表面积, $M$ 为侧面积, $h$ 为高, $A_G$ 为底面积.

(1)多面体 是由平面多边形所界的立体.

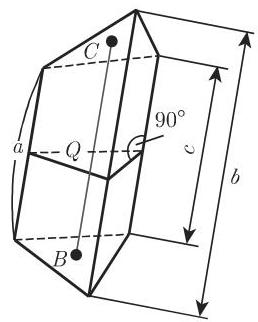
(2)棱柱(图 3.53)是具有两个全等的底并且以平行四边形作为侧面的多面体, 正棱柱是以正多边形作为底的直棱柱. 对于棱柱成立以下公式:

$$\begin{array}{}\text{(3.116)}& V=A_{G}h\end{array}$$$$\begin{array}{}\text{(3.117)}& M=pl,\end{array}$$$$\begin{array}{}\text{(3.118)}& S=M+2A_G,\end{array}$$

这里 $p$ 是与棱垂直的横截面周长, $l$ 是棱长. 如果棱仍彼此平行,但底不平行, 则侧面是梯形. 如果三角棱柱的底彼此不平行, 则它的体积可以用下列公式计算

(图 3.54):

$$\begin{array}{}\text{(3.119)}& V=\frac{\left(a+b+c\right)Q}{3},\end{array}$$

其中 $Q$ 是垂直的横截面面积, $a,b$ 和 $c$ 是平行的棱之长. 如果棱柱的底不平行,则其体积是

$$\begin{array}{}\text{(3.120)}& V=lQ,\end{array}$$

其中 $l$ 是连接两底重心的线段 $\overline{BC}$ 之长,而 $Q$ 则是与该线垂直的横截面面积.

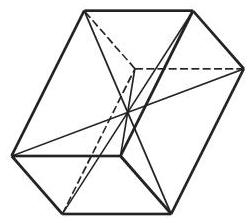
(3)平行六面体 是以平行四边形作为底的棱柱 (图 3.55), 即它被六个平行四边形所界. 在平行六面体中, 全部四条空间对角线彼此交于同一点, 即它们的中点.

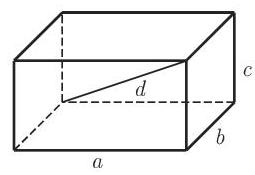
(4) 长方体 是以矩形为底的直角平行六面体. 在长方体中 (图 3.56), 空间对角线的长相等. 如果 $a,b$ 和 $c$ 是长方体的棱长, $d$ 是对角线长,则有

$$\begin{array}{}\text{(3.121)}& d^2=a^2+b^2+c^2,\end{array}$$$$\begin{array}{}\text{(3.122)}& V=abc,\end{array}$$$$\begin{array}{}\text{(3.123)}& S=2\left(ab+bc+ca\right).\end{array}$$

(5) 立方体(或正六面体) 是具有相等棱长的长方体: $a=b=c$ ,

$$\begin{array}{}\text{(3.124)}& d^2=3a^2,\end{array}$$$$\begin{array}{}\text{(3.125)}& V=a^3,\end{array}$$$$\begin{array}{}\text{(3.126)}& S=6a^2.\end{array}$$

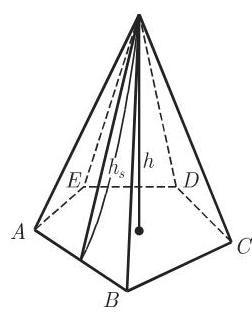
(6) 棱锥(图 3.57) 是底为多边形, 侧面为具有公共点, 即顶点的三角形的多面体. 如果从顶点到底 $A_G$ 的垂足位于底的中点,则称它为直棱锥. 如果直棱锥的底是一个正多边形 (图 3.58) 并且当底是 $n$ 边形时有 $n$ 个侧面,则称它为正棱锥. 棱锥连同底一起有 $\left(n+1\right)$ 个面. 对于其体积有公式

$$\begin{array}{}\text{(3.127)}& V=\frac{A_{G}h}{3}\end{array}$$

成立. 关于正棱锥的侧面积有公式

$$\begin{array}{}\text{(3.128)}& M=\frac{1}{2}p{h}_s\end{array}$$

成立,其中 $p$ 表示底的周长, $h_s$ 表示一个侧面的高.

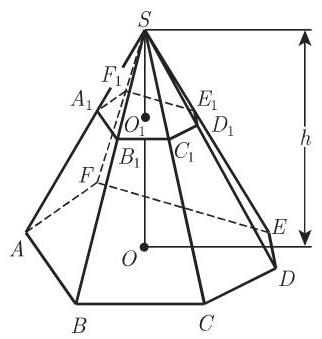
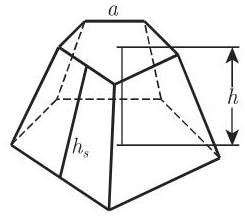
(7) 平截头棱锥体或截棱锥 是顶被一个平行于底的平面截去的棱锥 (图 3.57, 图 3.59). 用 $\overline{SO}$ 表示棱锥的高,即从顶到底的垂线,则有

$$\begin{array}{}\text{(3.129)}& \frac{{\overline{SA}}_1}{\overline{A_{1}A}}=\frac{{\overline{SB}}_1}{\overline{B_{1}B}}=\frac{{\overline{SC}}_1}{\overline{C_{1}C}}=\dots =\frac{{\overline{SO}}_1}{\overline{O_{1}O}},\end{array}$$$$\begin{array}{}\text{(3.130)}& \frac{\text{ 面积 }ABCDEF}{\text{ 面积 }{A}_1{B}_1{C}_1{D}_1{E}_1{F}_1}={\left(\frac{\overline{SO}}{\overline{S{O}_1}}\right)}^2\end{array}$$

成立. 如果 $A_D$ 和 $A_G$ 分别是上底和下底, $h$ 是截棱锥的高,即两底之间的距离,而 $a_D$ 和 $a_G$ 是这两底对应的边,则有

$$\begin{array}{}\text{(3.131)}& V=\frac{1}{3}h\left[A_G+A_D+\sqrt{A_G{A}_D}\right]=\frac{1}{3}h{A}_G\left[1+\frac{a_D}{a_G}+{\left(\frac{a_D}{a_G}\right)}^2\right].\end{array}$$

正截棱锥的侧面积是

$$\begin{array}{}\text{(3.132)}& M=\frac{p_D+p_G}{2}{h}_s,\end{array}$$

其中 $p_D$ 和 $p_G$ 是底的周长, $h_s$ 是侧面的高.

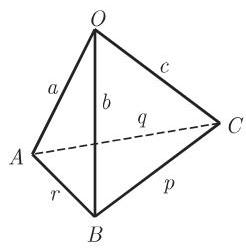
(8) 四面体 是一个三角棱锥 (图 3.60). 使用记号

$\overline{OA}=a,\overline{OB}=b,\overline{OC}=c,\overline{CA}=q,\overline{BC}=p,\overline{AB}=r,$

则下列公式成立

$$\begin{array}{}\text{(3.133)}& V^2=\frac{1}{288}\left|\begin{array}{ccccc}0& r^2& q^2& a^2& 1\\ r^2& 0& p^2& b^2& 1\\ q^2& p^2& 0& c^2& 1\\ a^2& b^2& c^2& 0& 1\\ 1& 1& 1& 1& 0\end{array}\right|.\end{array}$$

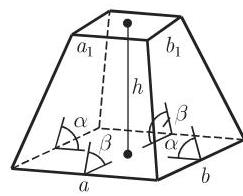
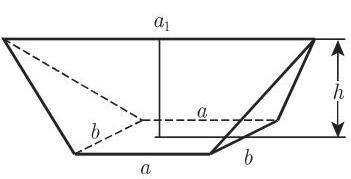
(9) 方尖形 是所有侧面都是不规则四边形的多面体. 在图 3.61 的特殊情形中, 两平行的底是矩形,相对的棱与底成相同的倾角,但它们没有公共点. 如果 $a,b$ 和 $a_1,b_1$ 是该方尖形两个底的边, $h$ 是它的高,则有

$$\begin{array}{}\text{(3.134)}& V=\frac{h}{6}\left[\left(2a+a_1\right)b+\left(2a_1+a\right)b_1\right]=\frac{h}{6}\left[ab+\left(a+a_1\right)\left(b+b_1\right)+a_1{b}_1\right].\end{array}$$

(10) 楔 是底为矩形的一个多面体, 其侧面是两个相对的等腰三角形和两个相对的等腰梯形 (图 3.62). 关于它的体积有公式

$$\begin{array}{}\text{(3.135)}& V=\frac{1}{6}\left(2a+a_1\right)bh.\end{array}$$

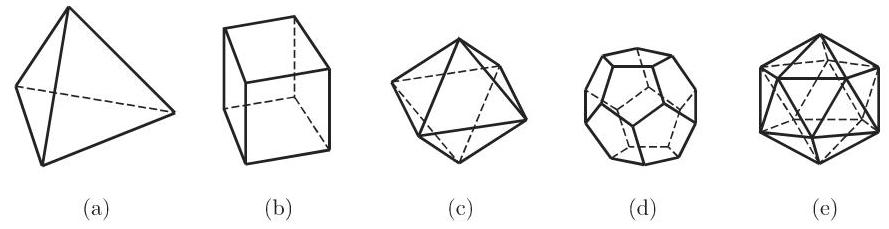
(11) 正多面体 具有全等的正多边形作为界面并具有全等的正则隅角. 图 3.63 中表示的是五种可能的正多面体; 表 3.7 显示的是相应数据.

(12) 欧拉关于多面体的定理 如果 $e$ 是一个凸多面体的顶点数, $f$ 是面数, $k$ 是棱数, 则

$$\begin{array}{}\text{(3.136)}& e-k+f=2\text{.}\end{array}$$

例子由表 3.7 给出.

名称	面的数目和形状	棱数	顶点数	$\frac{S}{a^2}$	体积 $\frac{V}{a^3}$
正四面体	4 个正三角形	6	4	$\sqrt{3}=1.7321$	$\frac{\sqrt{2}}{12}=0.1179$
立方体	6 个正方形	12	8	$6=6.0$	$1=1.0$
正八面体	8 个正三角形	12	6	$2\sqrt{3}=3.4641$	$\frac{\sqrt{2}}{3}=0.4714$
正十二面体	12 个正五边形	30	20	$3\sqrt{5\left(5+2\sqrt{5}\right)}=20.6457$	$\frac{15+7\sqrt{5}}{4}=7.6631$
正二十面体	20 个正三角形	30	12	$5\sqrt{3}=8.6603$	$\frac{5\left(3+\sqrt{5}\right)}{12}=2.1817$