Appearance
3.1.5 平面上的多边形
3.1.5.1 一般多边形
由直线段作为边所围成的一个封闭平面图形可以分解成
3.1.5.2 正凸多边形
正凸多边形 (图 3.23) 具有
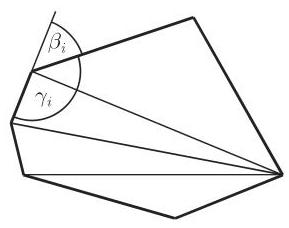
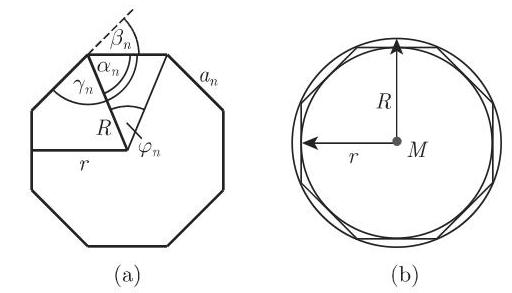
中心角
底角
外角
内角
外接圆半径
内切圆半径
边长
周长
3.1.5.3 某些正凸多边形
已将某些正凸多边形的性质汇集在表 3.2 中.
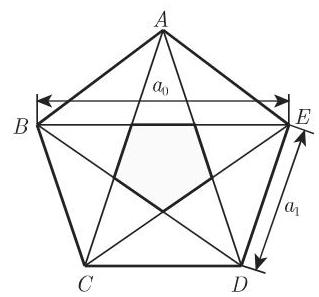
五边形和五角星形值得特别注意, 据信梅塔蓬图姆的希帕索斯 (约公元前 450) 通过这些多边形的性质 (参见第 2 页 1.1.1.2) 认识到无理数. 下面的例子对此作了讨论.
考虑越来越小的嵌套五边形并有
正多边形 | ||||
三边形 | ||||
五边形 | ||||
六边形 | ||||
八边形 | ||||
十边形 |