15.5.2 小波

傅里叶变换没有定位性能, 即如果信号在一个位置发生了变化, 则傅里叶变换处处发生了变化, 不可能 “立刻” 识别发生变化的位置. 这个情况是基于傅里叶变换把信号分解成了平面波. 平面波通过三角函数刻画, 三角函数在任意长的时间内都以相同周期进行振荡. 但对于小波变换,有几乎可以自由选取的函数 $\psi$ ,小波(小局域波) 通过平移和伸缩分析信号.

例子见哈尔小波(图 15.28(a))和墨西哥草帽小波(图 15.28(b)).

$◼\mathbf{A}$ : 哈尔小波:

$$\begin{array}{}\text{(15.144)}& \psi =\{\begin{array}{ll}1,& 0\le x<\frac{1}{2},\\ -1,& \frac{1}{2}\le t\le 1,\\ 0,& \text{ 其他. }\end{array}\end{array}$$

$◼\mathbf{B}$:墨西哥草帽小波:

$$\begin{array}{}\text{(15.145)}& \psi \left(x\right)=-\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}{\mathrm{e}}^{-x^2/2}\end{array}$$$$\begin{array}{}\text{(15.146)}& =\left(1-x^2\right){\mathrm{e}}^{-x^2/2}.\end{array}$$

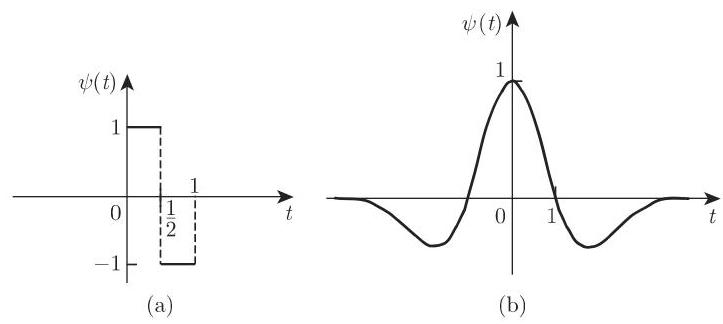
通常认为,任何函数 $\psi$ 可视为小波,如果函数二次可积,且根据 (15.143a),其傅里叶变换 $\mathrm{\Psi }\left(\omega \right)$ 生成正的有限积分

$$\begin{array}{}\text{(15.147)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\left|\mathrm{\Psi }\left(\omega \right)\right|}{\left|\omega \right|}\mathrm{d}\omega \end{array}$$

关于小波, 下述性质和定义非常重要:

(1)对于小波的均值, 有

$$\begin{array}{}\text{(15.148)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\psi \left(t\right)\mathrm{d}t=0.\end{array}$$

(2) 下述积分称为小波 $\psi$ 的 $k$ 阶矩:

$$\begin{array}{}\text{(15.149)}& {\mu }_k={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{t}^k\psi \left(t\right)\mathrm{d}t\end{array}$$

使得 ${\mu }_n\ne 0$ 的最小正整数 $n$ ,称为小波 $\psi$ 的阶.

$◼$ 对于哈尔小波 (15.144), $n=1$ ,对于墨西哥草帽小波 (15.146), $n=2$ .

(3) 若对任意 $k$ ,有 ${\mu }_k=0$ ,则 $\psi$ 是无限阶的. 具有有界支集的小波总是有限阶的.

(4) $n$ 阶小波与任何次数 $\le n-1$ 的多项式正交.