2.19.3 贯线算图

变量 $z_1,z_2,z_3$ 间的关系图可以通过赋予每个变量一个标度来实现 (参见第 149 页 2.17.1). $z_i$ 的标度方程为

$$\begin{array}{}\text{(2.295)}& x_i={\phi }_i\left(z_i\right),y_i={\psi }_i\left(z_i\right)\left(i=1,2,3\right),\end{array}$$

函数 ${\phi }_i,{\psi }_i$ 应使得满足算图方程的三个变量 $z_1,z_2,z_3$ 位于同一直线上. 为此,点 $\left(x_1,y_1\right),\left(x_2,y_2\right),\left(x_3,y_3\right)$ 构成的三角形面积必须为 0 (参见第 261 页 $\left(3.301\right))$ ,即必有

$$\begin{array}{}\text{(2.296)}& \left|\begin{array}{lll}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|=\left|\begin{array}{lll}{\phi }_1\left(z_1\right)& {\psi }_1\left(z_1\right)& 1\\ {\phi }_2\left(z_2\right)& {\psi }_2\left(z_2\right)& 1\\ {\phi }_3\left(z_3\right)& {\psi }_3\left(z_3\right)& 1\end{array}\right|=0.\end{array}$$

能够转化成形式 (2.296) 的三个变量 $z_1,z_2,z_3$ 间任意两个的关系都可用贯线算图表示.

接下来给出 (2.296) 的一些重要特例.

2.19.3.1 过一点具有三个直线标度的贯线算图

若零点是具有三个标度 $z_1,z_2,z_3$ 的直线的公共点,因为过原点的直线方程为 $y=mx$ ,则 (2.296) 的形式为

$$\begin{array}{}\text{(2.297)}& \left|\begin{array}{lll}{\phi }_1\left(z_1\right)& m_1{\phi }_1\left(z_1\right)& 1\\ {\phi }_2\left(z_2\right)& m_2{\phi }_2\left(z_2\right)& 1\\ {\phi }_3\left(z_3\right)& m_3{\phi }_3\left(z_3\right)& 1\end{array}\right|=0.\end{array}$$

计算行列式 (2.297), 有

$$\begin{array}{}\text{(2.298a)}& \frac{m_2-m_3}{{\phi }_1\left(z_1\right)}+\frac{m_3-m_1}{{\phi }_2\left(z_2\right)}+\frac{m_1-m_2}{{\phi }_3\left(z_3\right)}=0\end{array}$$

或

$$\begin{array}{}\text{(2.298b)}& \frac{C_1}{{\phi }_1\left(z_1\right)}+\frac{C_2}{{\phi }_2\left(z_2\right)}+\frac{C_3}{{\phi }_3\left(z_3\right)}=0,C_1+C_2+C_3=0,\end{array}$$

其中 $C_1,C_2,C_3$ 为常数.

• 方程 $\frac{1}{a}+\frac{1}{b}=\frac{2}{f}$ 是 (2.298b) 的一种特殊情况,它在光学、电阻的并联等中是一种重要关系. 相应的贯线算图由 3 条标度相同的直线构成.

2.19.3.2 具有两平行倾斜直线标度和一条倾斜直线标度的 贯线算图

其中第一个标度在 $y$ 轴上,第二个在与它距离为 $d$ 的平行线上,第三个标度在直线 $y=mx$ 上,此时 (2.296) 具有形式

$$\begin{array}{}\text{(2.299)}& \left|\begin{array}{ccc}0& {\psi }_1\left(z_1\right)& 1\\ d& {\psi }_2\left(z_2\right)& 1\\ {\phi }_3\left(z_3\right)& m{\phi }_3\left(z_3\right)& 1\end{array}\right|=0.\end{array}$$

按第一列展开计算行列式, 得到

$$\begin{array}{}\text{(2.300a)}& d\left(m{\phi }_3\left(z_3\right)-{\psi }_1\left(z_1\right)\right)+{\phi }_3\left(z_3\right)\left({\psi }_1\left(z_1\right)-{\psi }_2\left(z_2\right)\right)=0.\end{array}$$

因此

$$\begin{array}{}\text{(2.300b)}& {\psi }_1\left(z_1\right)\frac{{\phi }_3\left(z_3\right)-d}{{\phi }_3\left(z_3\right)}-\left({\psi }_2\left(z_2\right)-md\right)=0\text{ 或 }f\left(z_1\right)\cdot g\left(z_3\right)-h\left(z_2\right)=0.\end{array}$$

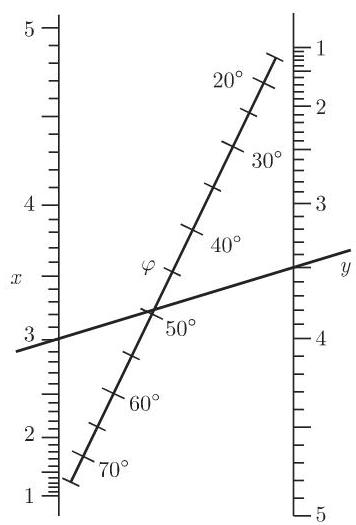
有时为了使用方便, 引入形如

$$\begin{array}{}\text{(2.300c)}& E_{1}f\left(z_1\right)\frac{E_2}{E_1}g\left(z_3\right)-E_{2}h\left(z_2\right)=0\end{array}$$

的分度标度 $E_1,E_2$ ,则 ${\phi }_3\left(z_3\right)=\frac{d}{1-\frac{E_2}{E_1}g\left(z_3\right)}$ . 可以选择 $E_2:E_1$ 使之满足第三个标度接近或集中在某一点. 令 $m=0$ ,则 $E_{2}h\left(z_2\right)={\psi }_2\left(z_2\right)$ ,且此时第三个标度线穿过第一个和第二个标度的起点. 因此这两个标度必须被方向相反的标度划分取代, 而第三个标度位于二者之间.

$◼xOy$ 面上一点的笛卡儿坐标 $x,y$ 与极坐标中相应角度 $\phi$ 之间的关系为

$$\begin{array}{}\text{(2.301)}& y^2=x^2{\tan }^2\phi \end{array}$$

对应的算图如图 2.110 所示. $x,y$ 的标度划分相同,但方向相反. 为了与二者之间的第三个标度有更好的交点, 其初始点要经过适当的平移. 第三个标度与第一个或第二个标度的交点分别为记为 $\phi =0^{\circ }$ 或 $\phi ={90}^{\circ }$ .

$◼$ 例如,当 $x=3,y=3.5$ 时,有 $\phi \approx {49.5}^{\circ }$ .

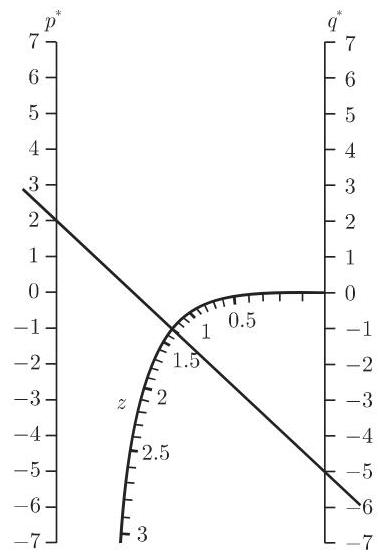
2.19.3.3 具有两平行直线和一条曲线标度的贯线算图

其中一个直线标度在 $y$ 轴,另一个直线标度与它的距离为 $d$ ,则方程 (2.296) 具有形式

$$\begin{array}{}\text{(2.302)}& \left|\begin{array}{ccc}0& {\psi }_1\left(z_1\right)& 1\\ d& {\psi }_2\left(z_2\right)& 1\\ {\phi }_3\left(z_3\right)& {\psi }_3\left(z_3\right)& 1\end{array}\right|=0.\end{array}$$

因此

$$\begin{array}{}\text{(2.303a)}& {\psi }_1\left(z_1\right)+{\psi }_2\left(z_2\right)\frac{{\phi }_3\left(z_3\right)}{d-{\phi }_3\left(z_3\right)}-d\frac{{\psi }_3\left(z_3\right)}{d-{\phi }_3\left(z_3\right)}=0.\end{array}$$

设第一个标度为 $E_1$ ,第二个为 $E_2$ ,则 (2.303a) 变为

$$\begin{array}{}\text{(2.303b)}& E_{1}f\left(z_1\right)+E_{2}g\left(z_2\right)\frac{E_1}{E_2}h\left(z_3\right)+E_{1}k\left(z_3\right)=0,\end{array}$$

其中 ${\psi }_1\left(z_1\right)=E_{1}f\left(z_1\right),{\psi }_2\left(z_2\right)=E_{2}g\left(z_2\right)$ ,且

$$\begin{array}{}\text{(2.303c)}& {\phi }_3\left(z_3\right)=\frac{d{E}_{1}h\left(z_3\right)}{E_2+E_{1}h\left(z_3\right)},{\psi }_3\left(z_3\right)=-\frac{E_1{E}_{2}k\left(z_3\right)}{E_2+E_{1}h\left(z_3\right)}.\end{array}$$

$◼$ 简化的三次方程 $z^3+p^{\ast }z+q^{\ast }=0$ (参见 52 页 1.6.2.3) 的形式为 (2.303b). 经代换 $E_1=E_2=1,f\left(z_1\right)=q^{\ast },g\left(z_2\right)=p^{\ast },h\left(z_3\right)=z$ 后,用来计算曲线标度坐标的公式为 $x={\phi }_3\left(z\right)=\frac{d\cdot z}{1+z}$ 和 $y={\psi }_3\left(z\right)=-\frac{z^3}{1+z}$ .

图 2.111 仅为 $z$ 取正数时的曲线的标度,若用 $-z$ 代替 $z$ ,确定方程 $z^3+p^{\ast }z+$ $q^{\ast }=0$ 的正根后,可得到 $z$ 的负值. 复根 $u+\mathrm{i}v$ 也可由算图确定出来. 实根总存在, 记为 $z_1$ ,则复根的实部 $u=-\frac{z_1}{2}$ ,虚部 $v$ 可由方程 $3u^3-v^2+p^{\ast }=\frac{3}{4}{z}_1^2-v^2+p^{\ast }=0$ 得到.

$◼$ 例如, $y^3+2y-5=0$ ,即 $p^{\ast }=2,q^{\ast }=-5$ ,有 $z_1\approx 1.3$ .