3.1.4 平面四边形

3.1.4.1 平行四边形

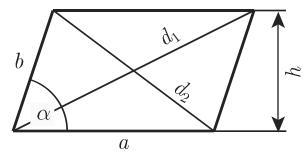
一个四边形如果具有以下属性就称为平行四边形 (图 3.15):

• 相对的边具有相同的长度,

• 相对的边互相平行,

• 对角线互相平分,

• 对角相等.

假设一个四边形的上述属性只有一个成立, 或假定一对对边相等且平行, 那么由此可推出所有其余的属性.

对角线, 边和面积之间的关系如下:

$$\begin{array}{}\text{(3.18)}& d_1^2+d_2^2=2\left(a^2+b^2\right)\end{array}$$$$\begin{array}{}\text{(3.19)}& h=b\sin \alpha ,\end{array}$$$$\begin{array}{}\text{(3.20)}& S=ah\text{.}\end{array}$$

3.1.4.2 矩形和正方形

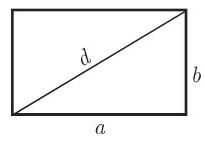
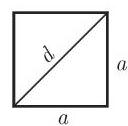
一个平行四边形如果是矩形 (图 3.16), 则它

• 只具有直角, 或

• 具有相同长度的对角线.

仅具有这些属性中的一个就够了, 因为它们中的任何一个都可以从另一个推出来. 只需证明平行四边形的一个角是直角, 则所有的角都是直角. 如果一个四边形具有四个直角, 则它是矩形.

矩形的周长 $U$ 和面积 $S$ 是

$$\begin{array}{}\text{(3.21a)}& U=2\left(a+b\right),\end{array}$$$$\begin{array}{}\text{(3.21b)}& S=ab.\end{array}$$

如果 $a=b$ 成立 (图 3.17),则矩形称为正方形,并有以下公式:

$$\begin{array}{}\text{(3.22)}& d=a\sqrt{2}\approx 1.414a,\end{array}$$$$\begin{array}{}\text{(3.23)}& a=d\frac{\sqrt{2}}{2}\approx 0.707d,\end{array}$$$$\begin{array}{}\text{(3.24)}& S=a^2=\frac{d^2}{2}.\end{array}$$

3.1.4.3 菱形

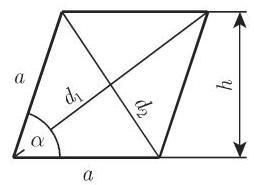
一个菱形 (图 3.18) 是一个平行四边形, 其中

• 所有的边具有相同长度, 或

• 对角线相互垂直, 或

• 对角线是平行四边形的角平分线.

上述属性中单独任何一个已足够; 其他所有的属性都可以从它推出来. 对于菱形, 有

$$\begin{array}{}\text{(3.25)}& d_1=2a\cos \frac{\alpha }{2},\end{array}$$$$\begin{array}{}\text{(3.26)}& d_2=2a\sin \frac{\alpha }{2},\end{array}$$$$\begin{array}{}\text{(3.27)}& d_1^2+d_2^2=4a^2.\end{array}$$$$\begin{array}{}\text{(3.28)}& S=ah=a^2\sin \alpha =\frac{d_1{d}_2}{2}.\end{array}$$

3.1.4.4 梯形

一个四边形如果有两边平行则称为梯形 (图 3.19). 平行的边称为底. 以 $a$ 和 $b$ 表示底, $h$ 表示高, $m$ 表示梯形的中位线(它是两非平行的边中点的连线),则有

$$\begin{array}{}\text{(3.29)}& m=\frac{a+b}{2},\end{array}$$$$\begin{array}{}\text{(3.30)}& S=\frac{\left(a+b\right)h}{2}=mh,\end{array}$$$$\begin{array}{}\text{(3.31)}& h_S=\frac{h\left(a+2b\right)}{3\left(a+b\right)}.\end{array}$$

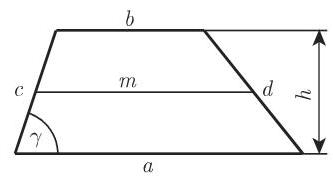
质心位于两平行的底 $a$ 和 $b$ 中点的连线上,与底 $a$ 的距离为 $h_S\left(3.31\right)$ . 关于用积分计算质心坐标, 见第 672 页 8.2.2.3,5..

对于等腰梯形有 $d=c$ .

$$\begin{array}{}\text{(3.32)}& S=\left(a-c\cos \gamma \right)c\sin \gamma =\left(b+c\cos \gamma \right)c\sin \gamma .\end{array}$$

3.1.4.5 一般四边形

由四条直线段所围的封闭平面图形称为一般四边形. 如果对角线全部位于该四边形内部, 则称它是凸四边形, 否则称其为凹四边形. 一般四边形可以被两条对角线 $d_1,d_2$ 中的每一条分成两个三角形 (图 3.20). 因此,每个四边形的内角之和是 $2\cdot {180}^{\circ }={360}^{\circ }$ .

$$\begin{array}{}\text{(3.33)}& \sum _{i=1}^4{\alpha }_i={360}^{\circ }.\end{array}$$

连接对角线中点 (图 3.20) 的线段 $m$ 之长由下式给出

$$\begin{array}{}\text{(3.34)}& a^2+b^2+c^2+d^2=d_1^2+d_2^2+4m^2.\end{array}$$

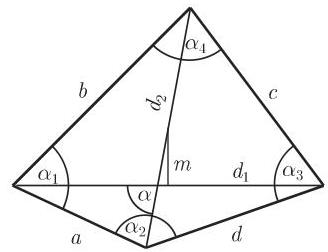
一般四边形的面积是

$$\begin{array}{}\text{(3.35)}& S=\frac{1}{2}{d}_1{d}_2\sin \alpha \end{array}$$

3.1.4.6 内接四边形

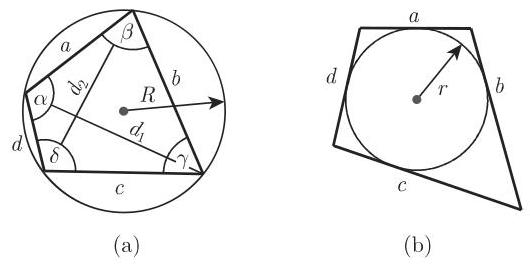
能被一个外接圆外接的四边形称为内接四边形 (图 3.21(a)), 其边是该圆的弦. 一个四边形是内接四边形当且仅当它的对角之和是 ${180}^{\circ }$ :

$$\begin{array}{}\text{(3.36)}& \alpha +\gamma =\beta +\delta ={180}^{\circ }.\end{array}$$

对于内接四边形, 有托勒密定理成立:

$$\begin{array}{}\text{(3.37)}& ac+bd=d_1{d}_2.\end{array}$$

内接四边形的外切圆半径是

$$\begin{array}{}\text{(3.38)}& R=\frac{1}{4S}\sqrt{\left(ab+cd\right)\left(ac+bd\right)\left(ad+cb\right)}.\end{array}$$

对角线可以通过以下公式计算:

$$\begin{array}{}\text{(3.39a)}& d_1=\sqrt{\frac{\left(ac+bd\right)\left(ab+cd\right)}{ad+bc}},\end{array}$$$$\begin{array}{}\text{(3.39b)}& d_2=\sqrt{\frac{\left(ac+bd\right)\left(ad+bc\right)}{ab+cd}}.\end{array}$$

面积可以用四边形半周长 $s=\frac{1}{2}\left(a+b+c+d\right)$ 来表示:

$$\begin{array}{}\text{(3.40)}& S=\sqrt{\left(s-a\right)\left(s-b\right)\left(s-c\right)\left(s-d\right)}.\end{array}$$

如果内接四边形也是一个外切四边形, 则

$$\begin{array}{}\text{(3.41)}& S=\sqrt{abcd}.\end{array}$$

3.1.4.7 外切四边形

如果一个四边形具有一个内切圆 (图 3.21(b)), 则称它为一个外切四边形, 并且边是该圆的切线. 一个四边形具有一个内切圆当且仅当对边长度之和相等, 并且这个和也等于半周长 $s$ :

$$\begin{array}{}\text{(3.42)}& s=\frac{1}{2}\left(a+b+c+d\right)=a+c=b+d.\end{array}$$

外切四边形的面积是

$$\begin{array}{}\text{(3.43)}& S=\left(a+c\right)r=\left(b+d\right)r,\end{array}$$

其中 $r$ 是内切圆的半径.