Appearance
3.2.2 大地测量学应用
3.2.2.1 测地坐标
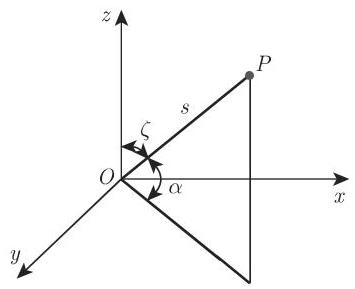
在几何学中通常使用右手坐标系来确定平面或空间中的点 (图 3.170). 与之相反, 在大地测量学中使用的是左手坐标系.
1. 测地直角坐标
在平面左手坐标系 (图 3.37) 中,表示横坐标的
如果除平面上一个点的位置外还要考虑它的高度, 那么我们可以使用三维左手直角坐标系(y, x, z),其中
2. 测地极坐标
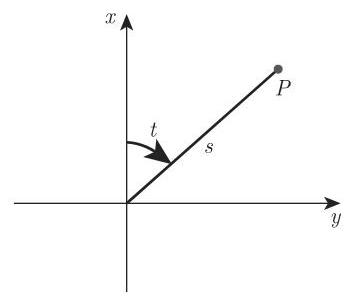
在大地测量学的左手平面极坐标系中 (图 3.38),一个点
为了确定高度,可以使用天顶角
3. 比例尺
在制图学中,比例因子
(1) 线段的换算 设
对于具有不同模数
(2) 面积的换算 如果面积按照公式
对于具有不同模数
3.2.2.2 大地测量学中的角
1. 新度
不同于数学 (参见第 170 页 3.1.1.5), 在大地测量学中用来度量角的单位是新度. 在这里, 周角或全角对应于 400 新度. 度与新度之间可以用表 3.5 中的公式进行转换.
1 全角 | |
1 直角 | |
1gon |
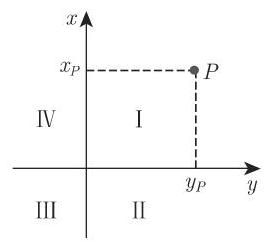
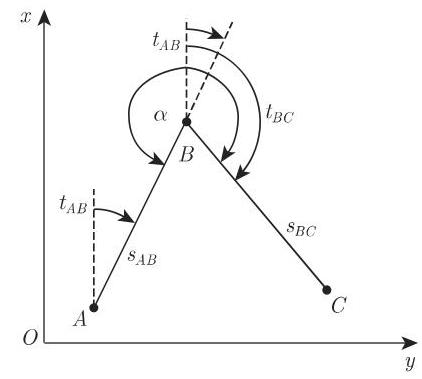
2. 方位角
在一点
象限 | I | II | III | IV |
计算器中的显示 | ||||
方位角 |
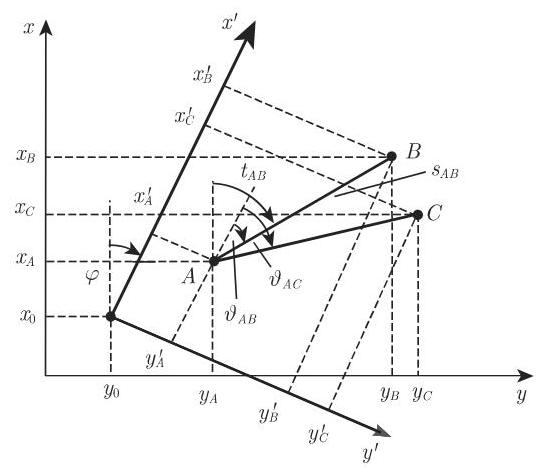
3. 坐标变换
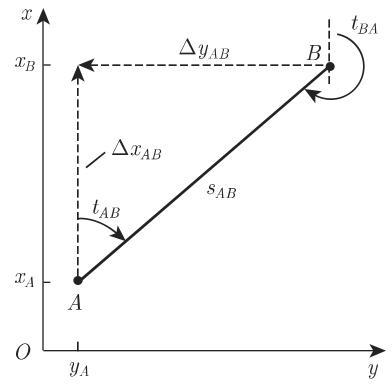
(1)从直角坐标计算极坐标 对于一个直角坐标系 (图 3.39) 中的两点
角
(2) 从距离和角计算直角坐标 在一个直角坐标系中,一个点
已知:
解
如果还测量了
(3) 两直角坐标系之间的坐标变换 为了在一张国家地图上定位一个给定点需要将本地坐标系
评论 下面两个公式可用作检验.
如果线段
3.2.2.3 测量中的应用
在大地测量学中,确定由三角测量定位的一点
1. 交会法
(1)经由两条定向直线的交会法或三角测量的第一基本问题 通过两个已知点
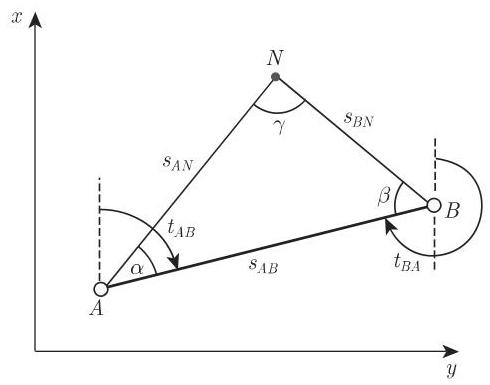
已知:
解
(2) 涉及不可见
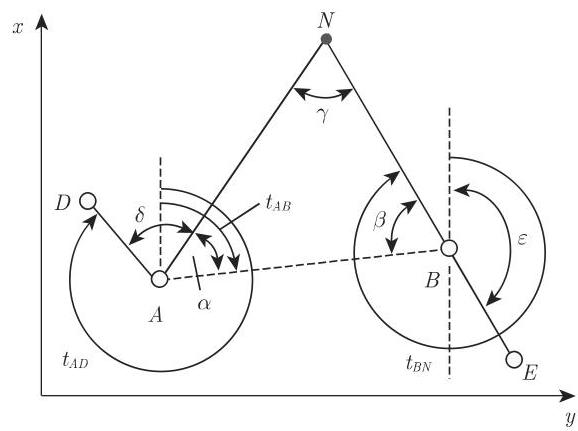
已知:
所测:
所求:
解 化为第一基本问题,根据 (3.110a) 计算
2. 后方交会法
(1) 后方交会法的斯涅耳问题 或通过三个已知点
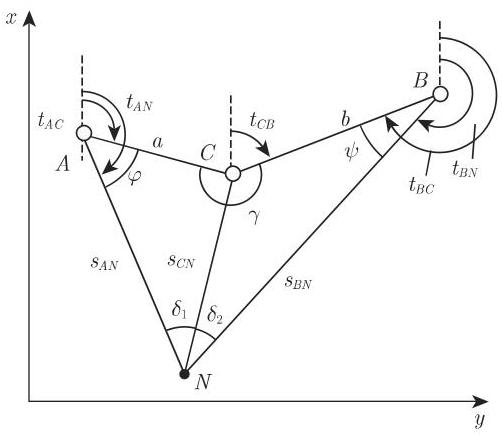
已知:
所测:
解
等式 (3.112f) 是确定
利用正弦定律 (3.88) 推出
代入(3.112g)有
由(3.112i)我们得到
由此我们可以确定下列线段和点:
(2) 卡西尼后方交会法
已知:
所测:
这一方法要用到两个参考点
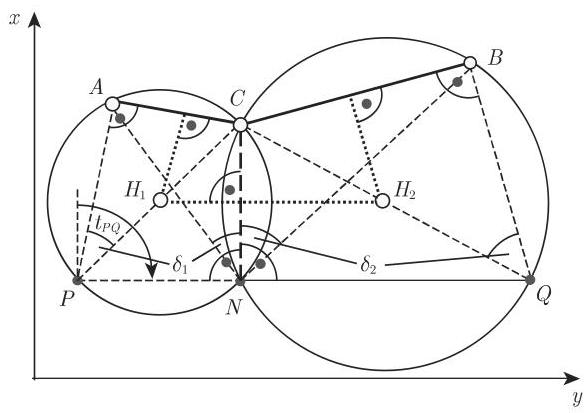
解
危险圆 在选取点时要保证它们不位于一个圆上, 因为那时将不存在解; 我们这里谈论的就是所谓的危险圆. 点越靠近危险圆, 该方法的精确性就越低.
3. 弧交会法
应用这一方法要确定一个所谓的新点
第二种解法 (这里不作讨论) 开始于将一般三角形分解为两个直角三角形.
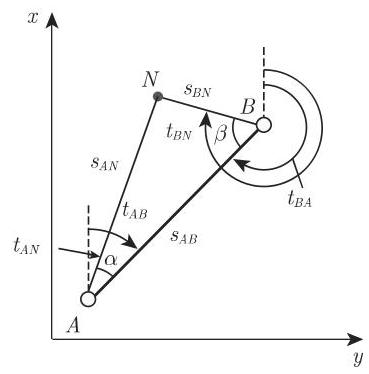
已知:
解