5.8.6 有向图中的路

1. 弧序列

有向图中一个弧序列 $F=\left(e_1,e_2,\cdots ,e_s\right)$ 称为一个长 $s$ 的链,当且仅当 $F$ 不两次含有任何一条弧并且每条弧 $e_i\left(i=2,3,\cdots ,s-1\right)$ 的端点之一是 $e_{i-1}$ 的一个端点,而另外一个是 $e_{i+1}$ 的一个端点.

一个链称作有向链,当且仅当对于 $i=1,2,\cdots ,s-1$ 弧 $e_i$ 的终点与 $e_{i+1}$ 的始点相重合.

遍历每个顶点至多一次的链或有向链分别称为基本链和基本有向链.

闭链称为圈. 一条闭有向路, 若它的每个顶点恰是两条弧的端点, 则称为环道.

• 图 5.60 包含不同种类的弧序列.

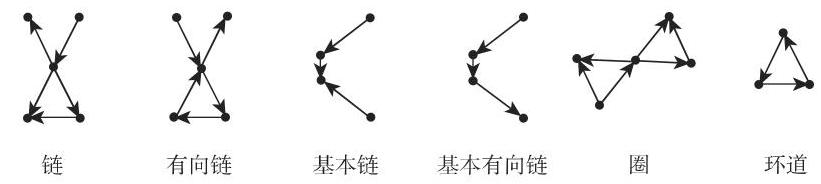
2. 连通图和强连通图

有向图 $G$ 称为连通的,当且仅当对于任何两个顶点存在一条连接它们的链. 图 $G$ 称为强连通的,当且仅当对于任何两个顶点 $v,w$ 存在一条给定的连接它们的有向链.

3. 丹齐格算法

设 $G=\left(V,E,f\right)$ 是一个加权简单有向图,并且对于每条弧 $e,f\left(e\right)>0$ . 下列算法产生 $G$ 的所有这样的顶点,它们通过有向链与一个固定顶点 $v_1$ 连接,并且它们与 $v_1$ 的距离:

a) 顶点 $v_1$ 有标号 $t\left(v_1\right)=0$ . 令 $S_1=\left\{v_1\right\}$ .

b) 被加标号的顶点的集合是 $S_m$ .

c) 如果 $U_m=\left\{e\mid e=\left(v_i,v_j\right)\in E,v_i\in S_m,v_j\notin S_m\right\}=\varnothing$ ,那么算法结束.

d) 不然我们选取弧 $e^{\ast }=\left(x^{\ast },y^{\ast }\right)$ 使得 $t\left(x^{\ast }\right)+f\left(e^{\ast }\right)$ 极小. 将 $e^{\ast }$ 和 $y^{\ast }$ 加标号,并且令 $t\left(y^{\ast }\right)=t\left(x^{\ast }\right)+f\left(e^{\ast }\right)$ ,以及 $S_{m+1}=S_m\cup \left\{y^{\ast }\right\}$ ,并且重复 b),其中 $m\text{:=}m+1$ .

(如果所有弧的权是 1, 那么可以应用关联矩阵 (参见第 541 页 5.8.2.1, 4.) 求出从顶点 $v$ 到顶点 $w$ 的最短有向链的长.)

如果 $G$ 的顶点 $v$ 未被加标号,那么不存在从 $v_1$ 到 $v$ 的有向路.

如果 $v$ 有标号 $t\left(v\right)$ ,那么 $t\left(v\right)$ 是这样的有向链的长. 在由被加标号的弧和顶点给出的树中可以找到从 $v_1$ 到 $v$ 的最短有向路,即对于 $v_1$ 的距离树.

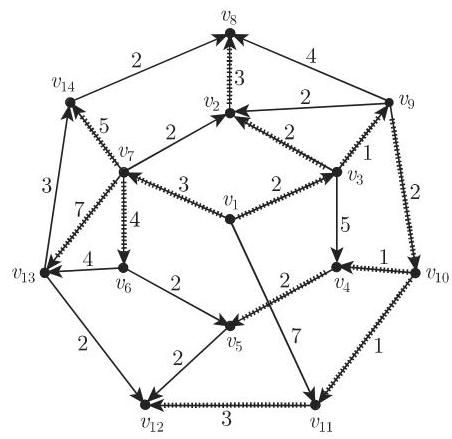
• 在图 5.61 中,加标号的弧和顶点表示图中对于 $v_1$ 的距离树. 最短有向链的长是

从 $v_1$ 到 $v_3:2$ ,从 $v_1$ 到 $v_6:7$ ,

从 $v_1$ 到 $v_7:3$ ,从 $v_1$ 到 $v_8:7$ ,

从 $v_1$ 到 $v_9:3$ ,从 $v_1$ 到 $v_{14}:8$ ,

从 $v_1$ 到 $v_2:4$ ,从 $v_1$ 到 $v_5:8$ ,

从 $v_1$ 到 $v_{10}:5$ ,从 $v_1$ 到 $v_{12}:9$ ,

从 $v_1$ 到 $v_4:6$ ,从 $v_1$ 到 $v_{13}:10$ ,

从 $v_1$ 到 $v_{11}:6$ .

注 在 $G=\left(V,E,f\right)$ 有带负权的弧的情形,还有一个修饰的求最短有向链的算法.