Appearance
8.3.2 第二类线积分
8.3.2.1 定义
第二类线积分或投影积分,如在
的定积分
或
其中
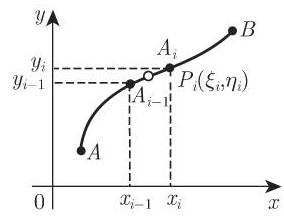
1. 在
有
2. 在
3. 在
8.3.2.2 存在定理
若函数
8.3.2.3 第二类线积分的计算
为了计算第二类线积分, 可将其化为定积分.
1. 以参数形式给出的积分路径
若积分路径的参数方程为
则有下面的公式
对 (8.113b),有
其中
注 若积分路径反向,即点
2. 以显形式给出的积分路径
在平面曲线或空间曲线中, 积分路径方程为
其中