Appearance
17.1.2 常微分方程的定性理论
17.1.2.1 流的存在性, 相空间结构
1. 解的延拓
微分方程 (17.1) 称为自治的. 除了自治方程, 还存在一类方程, 其右端项显式地依赖于时间, 称为非自治方程,
令
(1) 温特纳 (Wintner) 和康蒂 (Conti) 法则 若在方程 (17.1) 中
(2) 延拓法则 若随着时间增加, 方程 (17.1) 的一个解始终有界, 则该解可延拓至整个
假设: 在下面的讨论中, 我们总是假设方程 (17.1) 的流是存在的.
2. 相图
a) 若
b) 方程 (17.1) 的任意两条轨线或者没有交点, 或者重合. 因此, 方程 (17.1) 的相空间可分解成不相交的轨线. 将相空间分解为不相交的轨线称为相图.
c) 不同于稳态解, 每条轨线都是正则光滑的曲线, 它可能闭合, 也可能不闭合.
3. 刘维尔定理
设
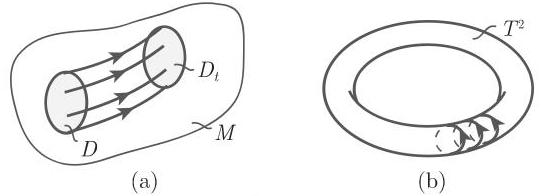
推论 若方程 (17.1) 中在
17.1.2.2 线性微分方程
1. 基本陈述
令
称为
称为对应的齐次一阶线性微分方程.
(1) 齐次线性微分方程组的基本定理 方程 (17.13a) 的任一解在整个
(2) 非齐次线性微分方程组的基本定理 方程 (17.13a) 的所有解全体构成
令
对任意解矩阵,或者在
(3) 常数变异法 令
2. 自治线性微分方程组
考虑微分方程
其中,
令
**a)
**b)
**c)
**d)
**e)
方程 (17.14) 满足当
其满足下面的性质:
a) 当
**b)
**c)
**d)
e) 对任意
f) 若
3. 周期系数的线性微分方程
考虑齐次线性微分方程 (17.13b),其中
令
17.1.2.3 稳定性理论
1. 李雅普诺夫稳定性与轨道稳定性
考虑非自治微分方程 (17.11). 方程 (17.11) 的解
解
对于自治微分方程 (17.1), 除了李雅普诺夫稳定性, 还有一些其他重要的稳定性概念. 方程 (17.1) 的解
- 给定
上的一个流,它的不变集是环面 . 在局部直角坐标系中,该流可表示为 ,其中, 是 周期的光滑函数,满足
满足初始条件
从上述表达式可以看出, 任意解是轨道稳定的, 但不是李雅普诺夫稳定的.
2. 李雅普诺夫渐近稳定性定理
标量函数
(1)
(2) 对任意
令
3. 稳态解的分类和稳定性
令
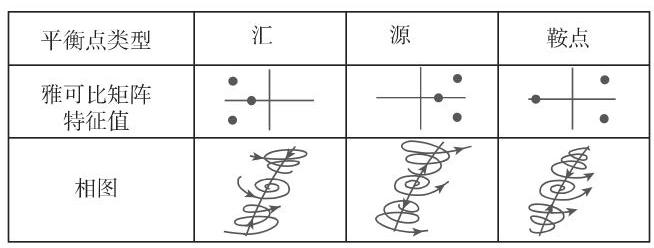
4. 周期轨的稳定性
设
其中,若
在
其中,最后一个乘法是
5. 周期轨的分类
若方程 (17.1) 的周期轨
根据安德罗诺夫-维特 (Andronov-Witt) 定理,方程 (17.1) 中(n - 1,0)型的双曲周期轨
是基解矩阵的弗洛凯表示. 从而,有
6. 极限集、极限环的性质
当
a) 集合
b) 若
例如,若
对于平面自治微分方程 (17.1)(即
庞加莱-本迪克松定理 令
因此, 对于平面自治微分方程, 除了平衡点或周期轨, 不存在更复杂的吸引子.
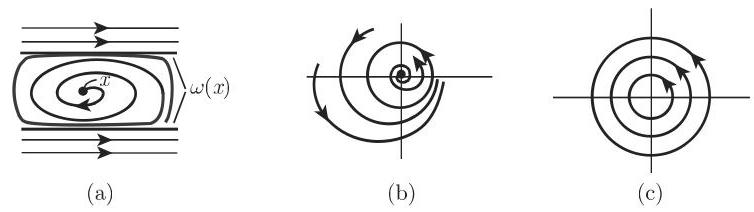
方程 (17.1) 的周期轨
7.
微分方程 (17.1) 可能存在
17.1.2.4 不变流形
1. 定义、分界面
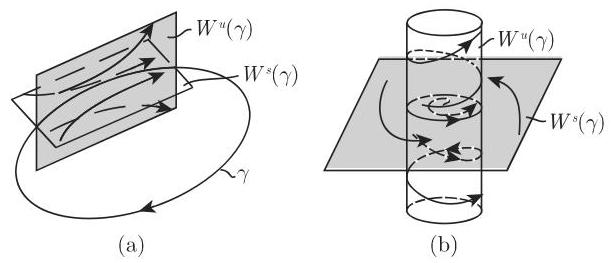
设
稳定流形和不稳定流形也称为分界面.
- 在平面上, 考虑微分方程
方程 (17.19a) 满足
方程 (17.19a) 中平衡点(0,0)的稳定流形和不稳定流形为
设
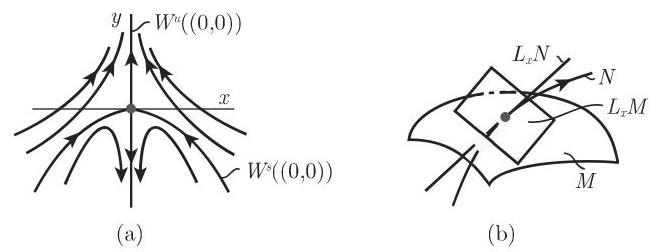
2. 阿达马-佩龙定理
阿达马-佩龙 (Hadamard-Perron) 定理给出了分界面的重要性质.
设
a) 流形
b) 若
和不稳定向量子空间
c) 若
令
其中,参数
在柱坐标变换
分界面如图 17.6 所示.
3.
考虑当
参数域 | 平衡点类型 | 特征多项式根 | ||
稳定结点 | ||||
稳定焦点 |
参数域 | 平衡点类型 | 特征多项式根 | ||
不稳定 结点 | ||||
不稳定 焦点 |
参数域 | 平衡点类型 | 特征多项式根 | ||
稳定 结点 | ||||
稳定 焦点 |
续表
参数域 | 平衡点类型 | 特征多项式根 | ||
稳定 节点 | ||||
稳定 焦点 |
 |  |
4. 同宿轨和异宿轨
设
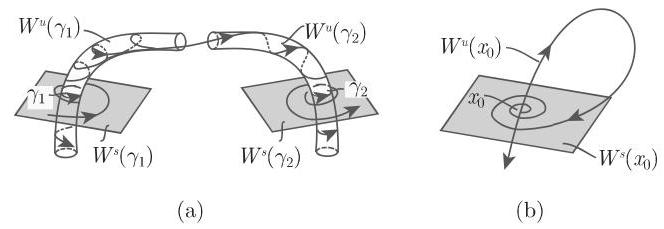
给定参数
17.1.2.5 庞加莱映射
1. 自治微分方程组的庞加莱映射
令
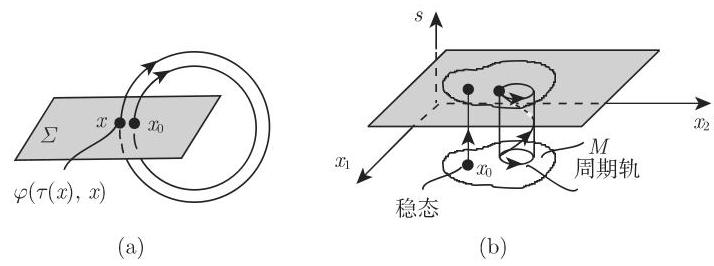
当
在极坐标下, 考虑方程 (17.9a) 的横截超平面
选定
故
2. 非自治时间周期微分方程的庞加莱映射
考虑非自治微分方程 (17.11),右端项
17.1.2.6 微分方程的拓扑等价
1. 定义
除了方程 (17.1) 和相应的流
其中,
微分方程组 (17.1) 和 (17.22) (或它们的流) 称为拓扑等价, 如果存在同胚映射
在拓扑等价的情形下, 方程 (17.1) 的平衡点对应于方程 (17.22) 的平衡点; 方程 (17.1) 的周期轨对应于方程 (17.22) 的周期轨, 但周期不一定相同. 因此, 若微分方程 (17.1) 和 (17.22) 拓扑等价, 则相空间中轨道分解的拓扑结构是相同的. 若方程 (17.1) 和 (17.22) 拓扑等价,并且同胚映射
拓扑等价或拓扑共轭也可在相空间
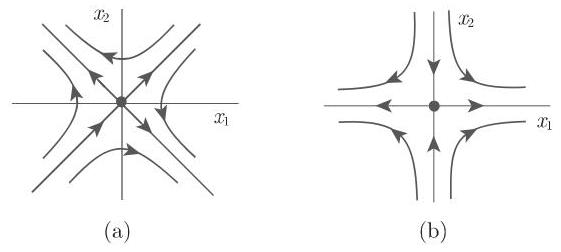
图 17.9(a) 和图 17.9(b) 相图中的流是拓扑等价的; 图 17.9(a) 和图 17.9(c) 相图中的流不是拓扑等价的
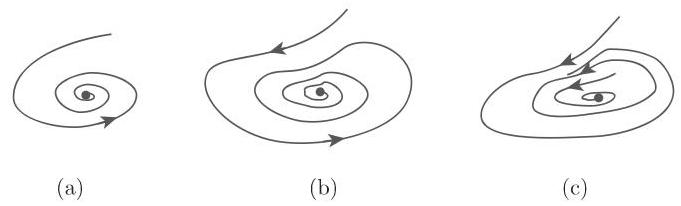
所示.
同胚映射
2. 格罗布曼-哈特曼 (Grobman-Hartman) 定理
设