8.4.2 三重积分

三重积分是积分概念在三维区域的推广, 也称为体积积分.

8.4.2.1 三重积分的概念

1. 定义

在三维区域 $V$ 上三元函数 $f\left(x,y,z\right)$ 的三重积分的定义方法与二重积分类似, 记为

$$\begin{array}{}\text{(8.141)}& {\int }_{V}f\left(x,y,z\right)\mathrm{d}V={\iiint }_{V}f\left(x,y,z\right)\mathrm{d}z\mathrm{d}y\mathrm{d}x.\end{array}$$

可将体积 $V$ (图 8.38) 划分成一系列小体积 $\mathrm{\Delta }{V}_i$ ,作积 $f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{V}_i$ ,其中点 $P_i\left(x_i,y_i,z_i\right)$ 位于小体积的内部或边界. 随着体积 $V$ 的划分,当每个小体积的直径都趋于 0,它们的个数趋于 $\mathrm{\infty }$ 时,三重积分为所有 $f\left(x_i,y_i,z_i\right)$ 与这些小体积乘积 $f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{V}_i$ 的和的极限. 仅当该极限与体积的划分方法及点 $P_i\left(x_i,y_i,z_i\right)$ 的取法无关时, 三重积分才存在, 且有

$$\begin{array}{}\text{(8.142)}& {\int }_{V}f\left(x,y,z\right)\mathrm{d}V=\underset{\begin{array}{c}\mathrm{\Delta }{V}_i\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left(x_i,y_i,z_i\right)\mathrm{\Delta }{V}_i.\end{array}$$

1. 平面图形的面积2. 曲面面积3. 柱体体积4. 平面图形关于$x$轴的转动惯量5. 平面图形关于极点0的转动惯量6. 密度函数为 $\varrho$ 的平面图形的质量7. 质地均匀的平面图形的重心坐标

2. 存在定理

三重积分的存在定理与二重积分的存在定理完全类似.

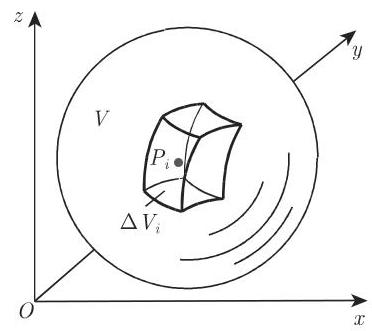
8.4.2.2 三重积分的计算

三重积分的计算可转化为依次计算三个普通积分. 若三重积分存在, 则其积分区域可进行任意划分.

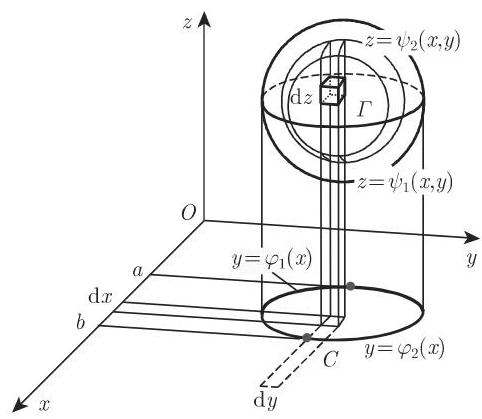
1. 笛卡儿坐标系下的计算

在此可把积分区域看成体积 $V$ ,用坐标曲面,如平面,把 $V$ 划分成一系列无穷小的平行六面体,使其直径为无穷小量 (图 8.39),接下来对所有乘积 $f\left(x,y,z\right)\mathrm{d}V$ 作和. 这要求首先沿着竖列作和,即关于 $z$ 作和,然后在小薄片的列中关于 $y$ 作和, 最后对所有这样的薄片作和,即关于 $x$ 作和. 任何列的和都是一个积分的近似和,若每个平行六面体的直径都趋于 0 , 则其和往往对应相应的积分, 进一步若被积函数连续, 则此累次积分等于三重积分, 其解析表达式为

$${\int }_{V}f\left(x,y,z\right)\mathrm{d}V={\int }_a^b\left\{{\int }_{{\phi }_1\left(x\right)}^{{\phi }_2\left(x\right)}\left[{\int }_{{\psi }_1\left(x,y\right)}^{{\psi }_2\left(x,y\right)}f\left(x,y,z\right)\mathrm{d}z\right]\mathrm{d}y\right\}\mathrm{d}x$$$$\begin{array}{}\text{(8.143a)}& ={\int }_a^b{\int }_{{\phi }_1\left(x\right)}^{{\phi }_2\left(x\right)}{\int }_{{\psi }_1\left(x,y\right)}^{{\psi }_2\left(x,y\right)}f\left(x,y,z\right)\mathrm{d}z\mathrm{d}y\mathrm{d}x,\end{array}$$

其中 $z={\psi }_1\left(x,y\right)$ 和 $z={\psi }_2\left(x,y\right)$ 表示积分区域 $V$ 下曲面和上曲面方程 (参见图 8.39 中的极限曲线 $\mathrm{\Gamma }$ ); $\mathrm{d}x\mathrm{d}y\mathrm{d}z$ 是笛卡儿坐标系下的体积微元; 函数 $y={\phi }_1\left(x\right)$ 和 $y={\phi }_2\left(x\right)$ 为体积在 $xOy$ 面投影边界线 $C$ 的下上两部分方程; $x=a$ 和 $x=b$ 表示体积 $V$ (也可看作体积在 $xOy$ 面上的投影) 在 $x$ 轴坐标的极值. 对积分区域作如下假设: 设函数 ${\phi }_1\left(x\right)$ 和 ${\phi }_2\left(x\right)$ 在区间 $a\le x\le b$ 上有定义、连续,且满足不等式 ${\phi }_1\left(x\right)\le {\phi }_2\left(x\right)$ ; 函数 ${\psi }_1\left(x,y\right)$ 和 ${\psi }_2\left(x,y\right)$ 在区域 $a\le x\le b,{\phi }_1\left(x\right)\le y\le {\phi }_2\left(x\right)$ 上有定义且连续,且 ${\psi }_1\left(x,y\right)\le {\psi }_2\left(x,y\right)$ ,即 $V$ 中的每个点均满足关系式

$$\begin{array}{}\text{(8.143b)}& a\le x\le b,{\phi }_1\left(x\right)\le y\le {\phi }_2\left(x\right),{\psi }_1\left(x,y\right)\le z\le {\psi }_2\left(x,y\right).\end{array}$$

正如二重积分一样, 三重积分也可以改变积分顺序, 此时相应的极限函数也发生改变. (一般地, 最外侧的积分限一定为常数, 且任何积分限都可能仅含有外侧积分变量. )

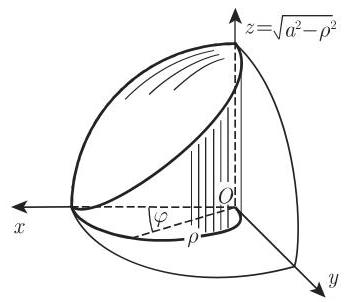
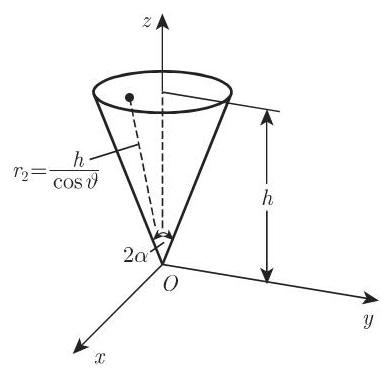
• 计算积分 $I={\int }_V\left(y^2+z^2\right)\mathrm{d}V$ ,其积分区域为坐标面与平面 $x+y+z=1$ 所围成的棱锥.

$$I={\int }_0^1{\int }_0^{1-x}{\int }_0^{1-x-y}\left(y^2+z^2\right)\mathrm{d}z\mathrm{d}y\mathrm{d}x$$$$={\int }_0^1\left\{{\int }_0^{1-x}\left[{\int }_0^{1-x-y}\left(y^2+z^2\right)\mathrm{d}z\right]\mathrm{d}y\right\}\mathrm{d}x=\frac{1}{30}.$$

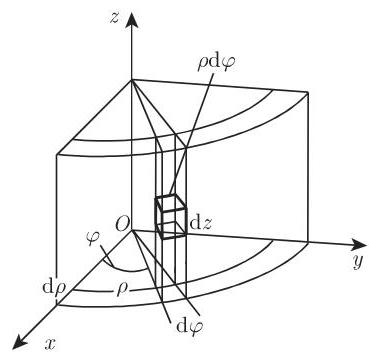
2. 柱面坐标系下的计算

用坐标曲面 $\rho =$ 常数, $\phi =$ 常数和 $z=$ 常数把积分区域分成无穷小的小体积 (图 8.40), 柱面坐标系下小区域的体积 (参见第 705 页表 8.11)

$$\begin{array}{}\text{(8.144a)}& \mathrm{d}V=\rho \mathrm{d}z\mathrm{d}\rho \mathrm{d}\phi \end{array}$$

用柱面坐标定义被积函数 $f\left(\rho ,\phi ,z\right)$ 之后,有积分

$$\begin{array}{}\text{(8.144b)}& {\int }_{V}f\left(\rho ,\phi ,z\right)\mathrm{d}V={\int }_{{\phi }_1}^{{\phi }_2}{\int }_{{\rho }_1\left(\phi \right)}^{{\rho }_2\left(\phi \right)}{\int }_{z_1\left(\rho ,\phi \right)}^{z_2\left(\rho ,\phi \right)}f\left(\rho ,\phi ,z\right)\rho \mathrm{d}z\mathrm{d}\rho \mathrm{d}\phi .\end{array}$$

$◼$计算积分 $I={\int }_V\mathrm{d}V$ (图 8.41),积分区域为以 $xOy$ 面、 $zOx$ 面、柱面 $x^2+y^2=ax$ 和球面 $x^2+y^2+z^2=a^2$ 所围成的立体: $z_1=0,z_2=\sqrt{a^2-x^2-y^2}=$$\sqrt{a^2-{\rho }^2};{\rho }_1=0,{\rho }_2=a\cos \phi ;{\phi }_1=0,{\phi }_2=\frac{\pi }{2}.I={\int }_0^{\pi /2}{\int }_0^{a\cos \phi }{\int }_0^{\sqrt{a^2-{\rho }^2}}\rho \mathrm{d}z\mathrm{d}\rho \mathrm{d}\phi$ $={\int }_0^{\pi /2}\left\{{\int }_0^{a\cos \phi }\left[{\int }_0^{\sqrt{a^2-{\rho }^2}}\mathrm{d}z\right]\rho \mathrm{d}\rho \right\}\mathrm{d}\phi =\frac{a^3}{18}\left(3\pi -4\right).$

当 $f\left(\rho ,\phi ,z\right)=1$ 时,该积分等于立体的体积.

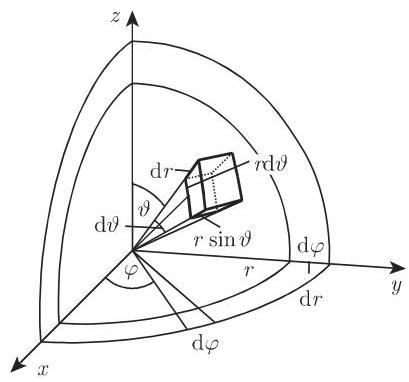
3. 球面坐标系下的计算

用坐标曲面 $r=$ 常数, $\phi =$ 常数和 $\vartheta =$ 常数把积分区域分成无穷小的小体积 (图 8.42), 球面坐标系下小区域的体积 (参见第 705 页表 8.11)

$$\begin{array}{}\text{(8.145a)}& \mathrm{d}V=r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi \end{array}$$

若在球面坐标下被积函数为 $f\left(r,\phi ,\vartheta \right)$ ,则

$$\begin{array}{}\text{(8.145b)}& {\int }_{V}f\left(r,\phi ,\vartheta \right)\mathrm{d}V={\int }_{{\phi }_1}^{{\phi }_2}{\int }_{{\vartheta }_1\left(\phi \right)}^{{\vartheta }_2\left(\phi \right)}{\int }_{r_1\left(\vartheta ,\phi \right)}^{r_2\left(\vartheta ,\phi \right)}f\left(r,\phi ,\vartheta \right)r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi .\end{array}$$

$◼$ 计算积分 $I={\int }_V\frac{\cos \vartheta }{r^2}\mathrm{d}V$ ,积分区域是以原点为顶点, $z$ 轴为对称轴,顶角为 $2\alpha$ , 高为 $h$ 的圆锥 (图 8.43),因此:

$$r_1=0,r_2=\frac{h}{\cos \vartheta };{\vartheta }_1=0,{\vartheta }_2=\alpha ;{\phi }_1=0,{\phi }_2=2\pi .$$$$I={\int }_0^{2\pi }{\int }_0^{\alpha }{\int }_0^{h/\cos \vartheta }\frac{\cos \vartheta }{r^2}{r}^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi$$$$={\int }_0^{2\pi }\left\{{\int }_0^{\alpha }\cos \vartheta \sin \vartheta \left[{\int }_0^{h/\cos \vartheta }\mathrm{d}r\right]\mathrm{d}\vartheta \right\}\mathrm{d}\phi$$$$=2\pi h\left(1-\cos \alpha \right)\text{.}$$

4. 任意曲线坐标系 $u,v,w$ 下的计算

坐标方程定义为

$$\begin{array}{}\text{(8.146)}& x=x\left(u,v,w\right),y=y\left(u,v,w\right),z=z\left(u,v,w\right)\end{array}$$

(参见第 350 页 3.6.3.1). 用坐标曲面 $u=$ 常数, $v=$ 常数和 $w=$ 常数把积分区域分成无穷小的小体积, 任意坐标系下小区域的体积 (参见第 705 页表 8.11)

$$\begin{array}{}\text{(8.147a)}& \mathrm{d}V=\left|D\right|\mathrm{d}u\mathrm{d}v\mathrm{d}w,\text{ 其中 }D=\left|\begin{array}{lll}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}& \frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}& \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u}& \frac{\partial z}{\partial v}& \frac{\partial z}{\partial w}\end{array}\right|\end{array}$$

即 $D$ 为雅可比行列式. 若在曲线坐标 $u,v,w$ 下被积函数为 $f\left(u,v,w\right)$ ,则

$$\begin{array}{}\text{(8.147b)}& {\int }_{V}f\left(u,v,w\right)\mathrm{d}V={\int }_{u_1}^{u_2}{\int }_{v_1\left(u\right)}^{v_2\left(u\right)}{\int }_{w_1\left(u,v\right)}^{w_2\left(u,v\right)}f\left(u,v,w\right)\left|D\right|\mathrm{d}w\mathrm{d}v\mathrm{d}u.\end{array}$$

注(8.144b)和(8.145b)都是(8.147b)的特殊情况. 对柱面坐标,有 $D=\rho$ ; 对球面坐标有 $D=r^2\sin \vartheta$ .

若被积函数连续, 则在任意坐标系下都可以改变积分次序. 在选择曲线坐标系时, 应使得积分限 (8.147b) 的确定以及积分计算尽可能简单.

8.4.2.3 三重积分的应用

表 8.10 给出了三重积分的某些应用, 699 页的表 8.8 给出了不同坐标系下相应的面积微元, 表 8.11 给出了不同坐标系下相应的体积微元.

$x_C=\frac{{\int }_{V}x\mathrm{d}V}{V}=$ $y_C=\frac{{\int }_{V}y\mathrm{d}V}{V}=$ $z_C=\frac{{\int }_{V}z\mathrm{d}V}{V}=$

$\frac{\iiint x\mathrm{d}z\mathrm{d}y\mathrm{d}x}{\iiint \mathrm{d}z\mathrm{d}y\mathrm{d}x}$ $\frac{\iiint y\mathrm{d}z\mathrm{d}y\mathrm{d}x}{\iiint \mathrm{d}z\mathrm{d}y\mathrm{d}x}$ $\frac{\iiint z\mathrm{d}z\mathrm{d}y\mathrm{d}x}{\iiint \mathrm{d}z\mathrm{d}y\mathrm{d}x}$

$\frac{\iiint {\rho }^2\cos \phi \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}{\iiint \rho \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}$ $\frac{\iiint {\rho }^2\sin \phi \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}{\iiint \rho \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}$ $\frac{{\iiint }_{\rho }\rho z\mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}{{\iiint }_{\rho }\rho \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z}$

$\frac{\iint r^3{\sin }^2\vartheta \cos \phi \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }{\iiint r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }$ $\frac{\iiint r^3{\sin }^2\vartheta \sin \phi \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }{\iiint r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }$ $\frac{\iiint r^3\sin \vartheta \cos \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }{\iiint r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi }$

坐标	体积微元
笛卡儿坐标 $x,y,z$	$\mathrm{d}V=\mathrm{d}x\mathrm{d}y\mathrm{d}z$
柱面坐标 $\rho ,\phi ,z$	$\mathrm{d}V=\rho \mathrm{d}\rho \mathrm{d}\phi \mathrm{d}z$
球坐标 $r,\vartheta ,\phi$	$\mathrm{d}V=r^2\sin \vartheta \mathrm{d}r\mathrm{d}\vartheta \mathrm{d}\phi$
任意曲线坐标 $u,v,w$	$\mathrm{d}V=\left|D\right|\mathrm{d}u\mathrm{d}v\mathrm{d}w\left(D\text{为雅可比行列式}\right)$