Appearance
5.9.1 模糊逻辑的基本概念
5.9.1.1 模糊集合的解释
现实世界中经常有多种程度的不确知的或不明确的情况, “模糊” 这个词也意味着某种不确定性, 而模糊逻辑这个名称也是基于这种意义. 基本上存在两种不同类型的模糊性: 不明确性和不确知性. 在此有两个从属的概念: 模糊集合论和模糊测度论. 在下面来源于实际的引论中, 我们讨论模糊集的思想、方法和概念, 它们是多值逻辑的基本数学工具.
1. 经典集和模糊集的概念
经典的 (清晰) 集的概念是二值的, 并且经典的布尔集代数同构于二值命题逻辑. 令
它表示对于每个
模糊集的概念基于下面的思想: 将集合元素的从属关系考虑为一个语句, 这个语句的真值由区间
换言之: 对于每个元素
2. 模糊集的性质及其他定义
下面的性质可以从定义直接推出:
(E1) 清晰集可以解释为具有隶属等级 0 和 1 的模糊集.
(E2) 隶属等级大于零,即
集合
(E3) 全域
(E4) 离散表示或有序对表示: 如果全域
在 (5.330) 中分数线和加号仅有符号意义.
表 5.7 模糊集的表格表示
... | |||
... |
(E5) 超模糊集: 依扎德 (Zadeh) 的定义, 如果模糊集的隶属函数本身也是一个模糊集, 那么它称为超模糊集.
3. 模糊语言学
一个设定了语言值 (例如, “小” “中”或“大”) 的量称为语言量或语言变量. 每个语言值可以用模糊集, 例如, 用具有支撑 (5.328) 的隶属函数 (参见 5.9.1.2) 的图象刻画. 模糊集的个数 (在 “小” “中” “大” 的情形, 它们是 3 个) 取决于问题.
在 5.9.1.2 中语言变量用
5.9.1.2 实直线上的隶属函数
隶属函数可以用在 0 和 1 之间取值的函数作为模型. 它们对给定不同的集的全域中的点表示不同的隶属等级.
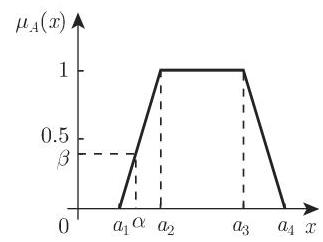
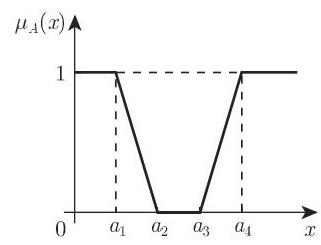
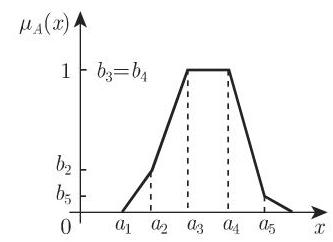
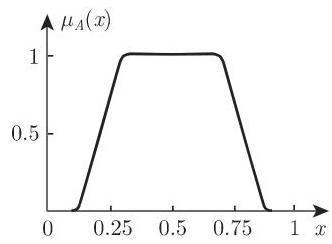
1. 梯形隶属函数
梯形隶属函数是普遍使用的. 下面的例子描绘了经常使用的分段 (连续可微) 隶属函数以及它们的特殊情形, 例如, 三角形隶属函数. 如果模糊量用连续或分段连续的的隶属函数表示, 那么相关的模糊量给出较光滑的输出函数.
如果
2. 钟形隶属函数
对于
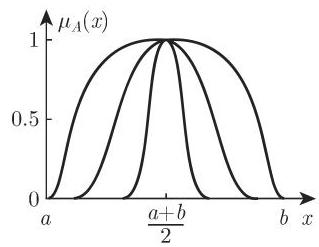
应用适当的正规化因子,对于 (例如)
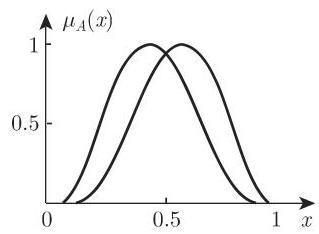
得到,其中
稍差一点的最简单的具有给定性质的多项式是
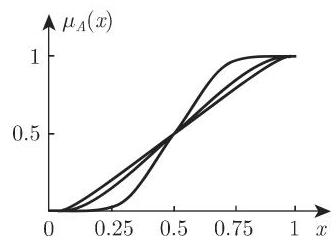
结束语 不精确的和非清晰的信息可以用模糊集描述, 并且可用隶属函数表示.
5.9.1.3 模糊集
1. 空模糊集和泛模糊集
a) 空模糊集
b) 泛模糊集
2. 模糊子集
如果
3. 实直线上模糊集容许区间和展形
如果
称为模糊集
4. 连续全域和离散全域上模糊集的转换
设全域是连续的, 并且模糊集在其上由隶属函数给定. 将全域离散化, 每个离散点与它的隶属值确定一模糊单元素集.
反之, 一个在离散全域上给定的模糊集通过隶属值在全域的离散点间插值可以转换为连续全域上的模糊集.
5. 正规和次正规模糊集
如果
如果
本节中给出的概念和方法限于正规模糊集, 但容易将它们扩充到次正规模糊集.
6. 模糊集的切割
模糊集
(5.338)
并且
(1) 性质.
a) 模糊集的
b) 支撑
c) 清晰 1 切割
(2) 表示定理.
反之,如果存在
(5.339b)
7. 模糊集
(1) 具有隶属函数
的模糊集,并且
的模糊集.
(2) 定理 如果具有隶属函数
那么它们模糊相似, 因为核等于 1 切割, 即
(3)