4.1.5 矩阵的运算法则

下列法则自然仅当运算可以实施时有效,例如,恒等矩阵 $\mathbf{I}$ 总具有与所给运算的要求相适应的大小.

1. 恒等矩阵与矩阵相乘

也称为恒等变换:

$$\begin{array}{}\text{(4.33)}& \mathbf{AI}=\mathbf{IA}=\mathbf{A}.\end{array}$$

(这不意味着交换律一般地成立,因为左边和右边的恒等矩阵 $\mathbf{I}$ 的大小可以不同.)

2. 标量矩阵 $\mathbf{S}$ 与方阵 $\mathbf{A}$ 相乘

标量矩阵 $\mathbf{S}$ 与方阵 $\mathbf{A}$ 相乘或者恒等矩阵 $\mathbf{I}$ 与方阵相乘,是可换的:

$$\begin{array}{}\text{(4.34a)}& \mathbf{AS}=\mathbf{SA}=c\mathbf{A}\text{ (其中 }\mathbf{S}\text{ 由 (4.8) 给出) }\end{array}$$$$\begin{array}{}\text{(4.34b)}& \mathbf{AI}=\mathbf{IA}=\mathbf{A}\end{array}$$

3. 零矩阵0与矩阵 $\mathbf{A}$ 相乘

零矩阵0与矩阵 $\mathbf{A}$ 相乘,结果是零矩阵:

$$\begin{array}{}\text{(4.35)}& \mathbf{A}\mathbf{0}=\mathbf{0},\mathbf{0}\mathbf{A}=\mathbf{0}\end{array}$$

(上面的零矩阵可以有不同的大小). 逆命题一般不成立,也就是说,由 $\mathbf{AB}=\mathbf{0}$ 推不出 $\mathbf{A}=\mathbf{0}$ 或 $\mathbf{B}=\mathbf{0}$ .

4. 两个矩阵之积为零

甚至两个矩阵 $\mathbf{A}$ 和 $\mathbf{B}$ 都不是零矩阵,它们的积可以是零矩阵:

$$\begin{array}{}\text{(4.36)}& AB=0\text{或}BA=0\text{或两者都成立,虽然}A\ne 0,B\ne 0\text{.}\end{array}$$$$\begin{array}{}\text{(4.37)}& \left(\mathbf{A}\mathbf{B}\right)\mathbf{C}=\mathbf{A}\left(\mathbf{B}\mathbf{C}\right),\end{array}$$

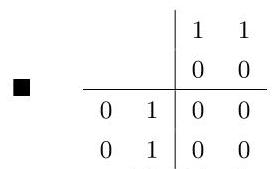
5. 三个矩阵相乘

即乘法结合律成立.

6. 两个矩阵之和或积的转置

$$\begin{array}{}\text{(4.38a)}& {(\mathbf{A}+\mathbf{B})}^{\mathrm{T}}={\mathbf{A}}^{\mathrm{T}}+{\mathbf{B}}^{\mathrm{T}},{\left(\mathbf{A}\mathbf{B}\right)}^{\mathrm{T}}={\mathbf{B}}^{\mathrm{T}}{\mathbf{A}}^{\mathrm{T}},{\left({\mathbf{A}}^{\mathrm{T}}\right)}^{\mathrm{T}}=\mathbf{A}.\end{array}$$

对于可逆方阵 ${\mathbf{A}}_{(n,n)}$ 有

$$\begin{array}{}\text{(4.38b)}& {\left({\mathbf{A}}^{\mathrm{T}}\right)}^{-1}={\left({\mathbf{A}}^{-1}\right)}^{\mathrm{T}}.\end{array}$$

7. 两个矩阵之积的逆

$$\begin{array}{}\text{(4.39)}& {\left(\mathbf{AB}\right)}^{-1}={\mathbf{B}}^{-1}{\mathbf{A}}^{-1}.\end{array}$$

8. 矩阵的幂

$$\begin{array}{}\text{(4.40a)}& {\mathbf{A}}^p=\underset{p\text{ 个因子 }}{\underbrace{\mathbf{A}\mathbf{A}\cdots \mathbf{A}}}\left(p>0\text{ 是整数 }\right).\end{array}$$$$\begin{array}{}\text{(4.40b)}& {\mathbf{A}}^0=\mathbf{I}\left(det\mathbf{A}\ne 0\right).\end{array}$$$$\begin{array}{}\text{(4.40c)}& {\mathbf{A}}^{-p}={\left({\mathbf{A}}^{-1}\right)}^p\left(p>0\text{ 是整数; }det\mathbf{A}\ne 0\right).\end{array}$$$$\begin{array}{}\text{(4.40d)}& {\mathbf{A}}^{p+q}={\mathbf{A}}^p{\mathbf{A}}^q\left(p,q\text{ 是整数 }\right).\end{array}$$

9. 克罗内克积

两个矩阵 $\mathbf{A}=\left(a_{\mu \nu }\right)\left(\left(m,n\right)\right)$ 型 $)\mathrm{与}=\left(b_{\mu \nu }\right)\left(\left(p,r\right)\right)$ 的克罗内克积按照法则

$$\begin{array}{}\text{(4.41)}& \mathbf{A}\otimes \mathbf{B}=\left(a_{\mu \nu }\mathbf{B}\right)\end{array}$$

定义. 由 $\mathbf{A}$ 的每个元素与矩阵 $\mathbf{B}$ 相乘,所得结果是一个 $\left(m\cdot p,n\cdot r\right)$ 型的新矩阵. $\mathbf{A}=\left(\begin{array}{ccc}3& -5& 0\\ 2& 1& 3\end{array}\right)$ 是(2,3)型矩阵, $\mathbf{B}=\left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)$ 是(2,2)型矩阵,

$$\mathbf{A}\otimes \mathbf{B}=\left(\begin{array}{ccc}3\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)& -5\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)& 0\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)\\ 2\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)& 1\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)& 3\cdot \left(\begin{array}{cc}1& 3\\ 2& -1\end{array}\right)\end{array}\right)$$$$=\left(\begin{array}{cccccc}3& 9& -5& -15& 0& 0\\ 6& -3& -10& 5& 0& 0\\ 2& 6& 1& 3& 3& 9\\ 4& -2& 2& -1& 6& -3\end{array}\right)$$

给出(4,6)型矩阵.

对于转置和迹下列等式成立:

$$\begin{array}{}\text{(4.42)}& {(\mathbf{A}\otimes \mathbf{B})}^{\mathrm{T}}={\mathbf{A}}^{\mathrm{T}}\otimes {\mathbf{B}}^{\mathrm{T}},\end{array}$$$$\begin{array}{}\text{(4.43)}& \mathrm{Tr}\left(\mathbf{A}\otimes \mathbf{B}\right)=\mathrm{Tr}\left(\mathbf{A}\right)\cdot \mathrm{Tr}\left(\mathbf{B}\right).\end{array}$$

10. 矩阵的微分

如果矩阵 $\mathbf{A}=\mathbf{A}\left(t\right)=\left(a_{\mu \nu }\left(t\right)\right)$ 具有参数 $t$ 的可微元素 $a_{\mu \nu }\left(t\right)$ ,那么它对于 $t$

的导数由

$$\begin{array}{}\text{(4.44)}& \frac{\mathrm{d}\mathbf{A}}{\mathrm{d}t}=\left(\frac{\mathrm{d}{a}_{\mu \nu }\left(t\right)}{\mathrm{d}t}\right)=\left(a_{\mu \nu }^{\prime }\left(t\right)\right)\end{array}$$

给出.